トポロジカルソートのアルゴリズム（閉路のない有向グラフDAGのソート）

2020年2月28日2020年9月2日グラフグラフ,有向グラフ,DAG,トポロジカルソート,BFS,DFS

トポロジカルソートとは、閉路の無い有向グラフ DAG について行うソートです。

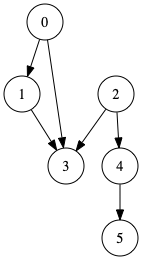
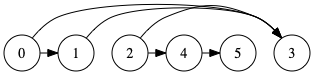
左図のDAGを右図のように頂点を一列に並べて、全ての辺の向きが左から右になるようにすることを言います。

アルゴリズム

トポロジカルソートのアルゴリズムには、幅優先探索(BFS)を利用したものと深さ優先探索(DFS)を利用したものの２つがあります。

※ このアルゴリズムでは、頂点に入る辺の数(入次数)に注目します。次数が0であれば、トポロジカルソートをした時に先頭に持ってこられることを利用してソートします。

※ 実際に左図のトポロジカルソートをしたDAGでは、先頭を見るとこのグラフに入る辺の数は0です。この先頭の頂点0を取り除くと、右図のようにまた先頭に入る辺の数は0になります。

※ 幅優先探索の時に、本当に入次数が0の頂点をグラフから削除するのは大変です。実際にはその頂点からのパスがある頂点について、入次数を1つ減らしてあげるだけで良いです。

※ 深さ優先探索では、探索時の帰りがけの順に注目します。
※どの頂点からDFSをはじめても、最後の頂点から帰ってくる順番は、トポロジカルソートをした時の後ろからの順番と同じになります。

※ 左図のように、頂点2 から深さ優先探索を行った時を考えてみます。まずは、3を探索し、その後は4→5と行ってから、5→4 と帰ってきます。この時の帰ってきた順に並べると上手く逆向きのトポロジカルソートができています。

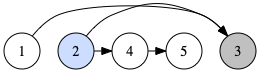
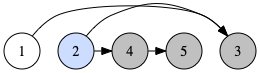
上の例では頂点1がまだ未探索なので、再び頂点1から深さ優先探索を始めれば良いです。その際は既に探索した頂点は探索しないようにしましょう。

計算量

• 幅優先探索：\(O(|V|+|E|)\)
• 深さ優先探索：\(O(|V|+|E|)\)

未探索の頂点ごとに深さ優先探索や幅優先探索を行うので、計算量はどちらも \(O(|V|+|E|)\) となります。

C++での実装例

幅優先探索でのアルゴリズム

グラフを受け取って、トポロジカルソートをした頂点のvectorを返す関数です。

#include <bits/stdc++.h>
using namespace std;
struct Edge {
    int to;
};
using Graph = vector<vector<Edge>>;

/* topo_sort(G): グラフG をトポロジカルソート
    返り値: トポロジカルソートされた頂点番号
    計算量: O(|E|+|V|)
 */
vector<int> topo_sort(const Graph &G) {  // bfs
    vector<int> ans;
    int n = (int)G.size();
    vector<int> ind(n);            // ind[i]: 頂点iに入る辺の数(次数)
    for (int i = 0; i < n; i++) {  // 次数を数えておく
        for (auto e : G[i]) {
            ind[e.to]++;
        }
    }
    queue<int> que;
    for (int i = 0; i < n; i++) {  // 次数が0の点をキューに入れる
        if (ind[i] == 0) {
            que.push(i);
        }
    }
    while (!que.empty()) {  // 幅優先探索
        int now = que.front();
        ans.push_back(now);
        que.pop();
        for (auto e : G[now]) {
            ind[e.to]--;
            if (ind[e.to] == 0) {
                que.push(e.to);
            }
        }
    }
    return ans;
}

深さ優先探索(DFS)でのアルゴリズム

グラフを受け取って、DFSでの帰りがけ順に頂点を ans に加えていきます。逆向きなので、最後に反転させましょう。

#include <bits/stdc++.h>
using namespace std;

struct Edge {
    int to;
};
using Graph = vector<vector<Edge>>;

/* topo_sort(G): グラフG をトポロジカルソート
    返り値: トポロジカルソートされた頂点番号
    計算量: O(|E|+|V|)
 */
void dfs(const Graph &G, int v, vector<bool> &used, vector<int> &ans) {
    used[v] = true;
    for (auto e : G[v]) {
        if (!used[e.to]) {
            dfs(G, e.to, used, ans);
        }
    }
    ans.push_back(v);  // 帰りがけにpush_back
}
vector<int> topo_sort(const Graph &G) {  // bfs
    vector<int> ans;
    int n = (int)G.size();
    vector<bool> used(n, false);
    for (int v = 0; v < n; v++) {  // 未探索の頂点ごとにDFS
        if (!used[v]) dfs(G, v, used, ans);
    }
    reverse(ans.begin(), ans.end());  // 逆向きなのでひっくり返す
    return ans;
}

参考

BFSとDFSのどちらが良いのか？

書きやすさの面では、深さ優先探索のほうがやりやすいかもしれません。しかし、再帰関数で実装した場合は、再帰が深くなるとスタックオーバーフローとなる可能性があります。

再帰が深くなりそうな大きいグラフの場合は、幅優先探索でのアルゴリズムのほうが良いでしょう。

閉路のない有向グラフ DAG との関係

実は以下の同値関係が成り立ちます。

グラフ G は閉路の無い有向グラフ DAG である ⇔ グラフ G はトポロジカルソートできる

閉路があるときはトポロジカルソートを行うことができません。これをうまく利用すると、閉路を検出することもできます。

先程の幅優先探索のコードでは、返り値のvector のサイズをみて、グラフの頂点数と等しければ閉路がなく、等しくなければ閉路があることが分かります。

（深さ優先探索のコードではDAGであることを仮定したコードなので、閉路があった場合でも動作します。閉路の検出には更に変更が必要です。）

練習問題

• AOJ GRL_4_B Topological Sort：基本
• [AtCoder ]全国統一プログラミング王決定戦予選 D – Restore the Tree