Binary Indexed Tree (BIT) 総まとめ！区間加算や二次元BITまで

2020年3月5日データ構造転倒数,二次元BIT,BIT,区間和,競プロ,二分探索,セグメント木,区間,データ構造,RAQ,RSQ

Binary Indexed Tree (またはフェニック木) は 数列 \(a_1, a_2, a_3, \cdots, a_n\) が与えられた時に、以下のようなことがそれぞれ \(O(log n)\) で実現できるデータ構造のことです。

  1. i と x が与えられたとき、\(a_i \) に x を加算する
  2. i が与えられたとき、\(a_1 + a_2 + \cdots + a_i\) を求める

ナイーブな方法では、1つ目に \(O(1)\)・2つ目に \(O(n)\) の計算量が必要です。
また、1から i 番目までの区間和を保存する方法では、1つ目に \(O(n)\)・2つ目に \(O(1)\) の計算量が必要となってしまいます。

BITの気持ち

BITはセグメント木の機能を限定したようなもの

セグメント木と呼ばれるデータ構造でも、Binary Indexed Tree の代替になることができます。

以下の記事で解説したように、セグメント木を用いることで「区間加算」や「区間和」のクエリを \(O(log n)\) で求めることができるのです。

セグメント木を徹底解説！0から遅延評価やモノイドまで

しかし、セグメント木で求めることができるのは「任意の区間和」であり、BITで求められているのは「最初から i 番目までの区間和」です。セグメント木では過剰な機能となっています。

「最初から i 番目までの区間和」を求めるだけならば、以下の図においてセグメント木の以下の灰色の部分は無くても構いません。（それぞれのノードは区間和の値を保持しているとします。）

灰色の部分は無くても 1からi までの和を求めるのに問題はない

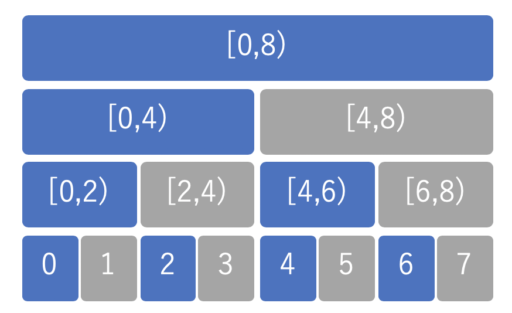
例えば、「0 から 6 番目までの和」を求める際は、以下のオレンジ部分を全て足し合わせるだけで良いはずです。

オレンジ部分の和が「0から6番目までの和」

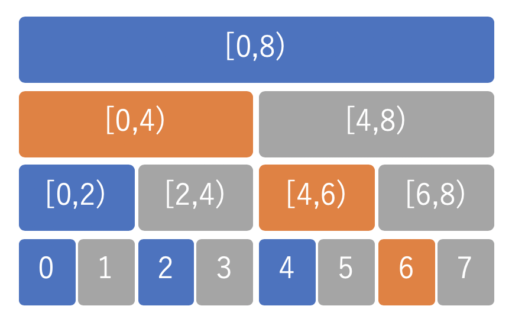
BIT を利用するのは、以上の考え方を用いてセグメント木よりも機能を限定することで、

  • 実装がより簡単
  • 定数倍高速に動作
  • より省メモリ

になるからなのです。

BIT の仕組み

BIT は以下のように、セグメント木の不要な部分を削除した形となっています。

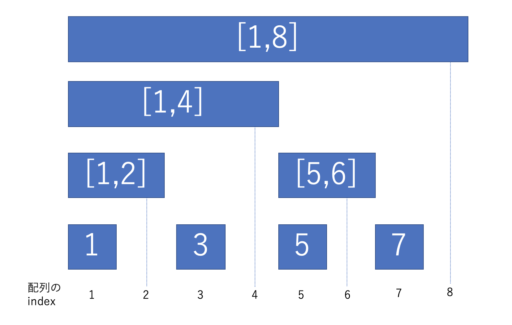
※ 0 始まり(0-indexed) ではなく 1 から番号を始めています(1-indexed)。また半開区間ではなく閉区間で考えます。これは後で計算をする際に楽になるため、このようにしています。

セグメント木は完全二分木で表現していましたが、BITでは保持するべき区間の量が約半分になったので、上図のようにサイズ N の配列を用いて表現することができます。

加算の方法

「i と x が与えられたとき、\(a_i \)に x を加算する」ことを考えてみましょう。

結論から言うと「i からはじめて、 i に最後の 1 が立っているビットを加算しながら、場所 i の値に x を加える」ことを繰り返せば良いです。（理由は後述します。）

例えば、5番目に値 x を加算する際は、以下のオレンジ色の部分に値を加算すれば良いです。

5番目に値を加算する

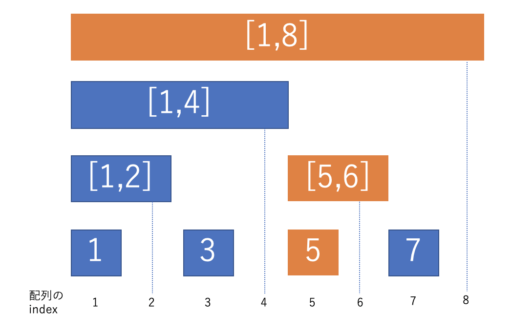
このとき、更新場所を2進数で考えると、

  • 5番目 (\(0101_2\)) に x を加算
  • 6番目 (\(0110_2 = 0101_2 + 0001_2\)) に x を加算
  • 8番目 (\(1000_2 = 0110_2 + 0010_2\)) に x を加算

のように、実際に最後に立っている 1 のビットを加算しながら次の地点を取得しています。

区間和取得の方法

「i が与えられたとき、\(a_1 + a_2 + \cdots + a_i\) を求める」ことを考えてみましょう。

こちらも結論から言うと先程と同様に、「i からはじめて、 i に最後の 1 が立っているビットを減算しながら、場所 i の値を合計していく」と良いです。

例えば、[1,7] の和を求める時は、以下のオレンジ色の部分の和を求めれば良いです。

[1,7] の和を求める

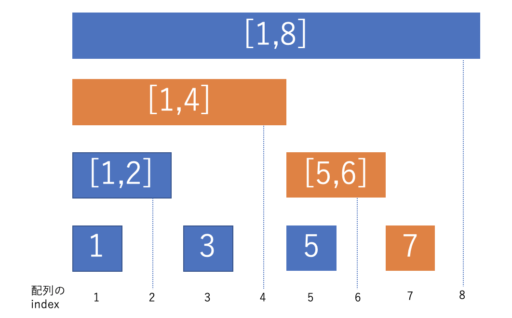
このとき、探索場所を2進数で考えると、

  • 7番目 (\(0111_2\))
  • 6番目 (\(0110_2 = 0111_2 – 0001_2\))
  • 4番目 (\(0100_2 = 0110_2 – 0010_2\))
  • 0番目 (\(0000_2 = 0100_2 – 0100_2\)) は無いので終了

のように、実際に最後に立っている 1 のビットを減算しながら次の地点を取得しています。

なぜ最後の 1 のビットを足したり引いたりして次の場所が求まるのか

場所ごとに最後の 1 のビットが下から何桁目にあるのかを良く見ると、

  • 最後の 1 のビットが下から 1 桁目 なら区間のサイズは 1 （ 1, 3, 5, 7 )
  • 最後の 1 のビットが下から 2 桁目 なら区間のサイズは 2 （ 2:[1,2], 6: [5,6] )
  • 最後の 1 のビットが下から 3 桁目 なら区間のサイズは 4 （ 4:[1,4] )
  • 最後の 1 のビットが下から 4 桁目 なら区間のサイズは 8 （ 8:[1,8]

のように、最後の 1 のビットがどこにあるのかを見ると、その場所にあったノードが表現する区間のサイズを得ることができます。

先程は、単純に区間のサイズを足し引きして、次の地点を得ていただけなのです。

なぜわざわざ2進数で考えたのか

区間のサイズを足し引きするだけならば、別に2進数で考える必要はありませんでした。

しかし、2進数で最後の1のビットを考えると、コンピュータでは以下のように AND 演算によって高速に計算をすることができます。

  • i の最後の1のビット = i & -i

これは、負の数が「ビット反転+1」で表現されることを利用したものです。

実際に、6 の最下位ビットは

  • 6 & -6 = \((00…0110_2)\) & \((11…1010_2)\) = \(00…0010_2\)

というように求めることができます。

BITの実装

以下コードを元に、BITの構造体を実装していきましょう。

template <typename T>
struct BIT {
    int n;          // 配列の要素数(数列の要素数+1)
    vector<T> bit;  // データの格納先(1-indexed)。初期値は0
    BIT(int n_) : n(n_ + 1), bit(n, 0) {}
    /*
    ここにメソッドを実装する
    */
};

1点加算

「i と x が与えられたとき、\(a_i \)に x を加算する」メソッドを追加しましょう。

「i からはじめて、 i に最後の 1 が立っているビットを加算しながら、場所 i の値に x を加える」ことを繰り返せば良いです。

void add(int i, T x) { // a_i += x とする
    for (int idx = i; idx < n; idx += (idx & -idx)) {
        bit[idx] += x;
    }
}

最初から i 番目までの和の取得

「i が与えられたとき、\(a_1 + a_2 + \cdots + a_i\) を求める」メソッドを追加しましょう。

「i からはじめて、 i に最後の 1 が立っているビットを減算しながら、場所 i の値を合計していく」だけで良いです。

T sum(int i) { // a_1 + a_2 + ... + a_i を計算する
    T s(0);
    for (int idx = i; idx > 0; idx -= (idx & -idx)) {
        s += bit[idx];
    }
    return s;
}

実装のまとめ

以上の実装をまとめると以下のようになります。

/* BIT: 区間和の更新や計算を行う構造体
    初期値は a_1 = a_2 = ... = a_n = 0
    ・add(i,x): a_i += x とする
    ・sum(i): a_1 + a_2 + ... + a_i を計算する
    計算量は全て O(logn)
*/
template <typename T>
struct BIT {
    int n;          // 配列の要素数(数列の要素数+1)
    vector<T> bit;  // データの格納先
    BIT(int n_) : n(n_ + 1), bit(n, 0) {}

    void add(int i, T x) {
        for (int idx = i; idx < n; idx += (idx & -idx)) {
            bit[idx] += x;
        }
    }

    T sum(int i) {
        T s(0);
        for (int idx = i; idx > 0; idx -= (idx & -idx)) {
            s += bit[idx];
        }
        return s;
    }
};

区間加算(RAQ)対応 BIT

遅延評価セグメント木で「区間更新」や「区間加算」に対応させましたが、BIT でも「区間 [l, r]に x を加算する」といった区間加算(RAQ: Range Add Query) を \(O(log n)\) で実現することができれば便利です。

区間加算の様子

区間 [l, r] に x を加算した後に、[1, i] までの区間の合計を取得することを考えてみましょう。

この値が加算前後でどのように変化しているのか、の様子を見ることで、実際にどのように実装すれば良いかのヒントになります。

以下では、加算前の合計値を sum(i) 、加算後の合計値を sum'(i) とすることにします。

\(1 \leq i < l\) の時

  • sum'(i) = sum(i)

[1, i] の区間の合計値は、x の加算前後で変化しません。

\(l \leq i \leq r\) の時

  • sum'(i) = sum(i) + \(x\cdot (i-l+1) \)
    = sum(i) + \(x i\) – \(x (l-1)\)

[1, l-1] の合計値は変化していませんが、[l, i] の合計値は \(x \cdot (i-l+1)\) だけ増加しています。

\(r < i\) の時

  • sum'(i) = sum(i) + \(x\cdot (r-l+1) \)
    = sum(i) + \(x r\) – \(x (l-1)\)

[1, l-1] の合計値は変化していませんが、[l, r] の合計値は \(x\cdot (r-l+1)\) だけ増加しています。[r+1, i] の合計値は変化していません。

区間加算の方法

セグメント木の場合と同様に、2つの BIT を持つことで RAQ に対応することができます。

先程見たように、i の値によって区間和の値を求める式は変化しました。結論から述べると、それらは以下のようにすると上手くいきます。

区間加算

  • BIT0 の l 番目に -\(x (l-1)\)を加算
  • BIT0 の r+1 番目に \(x r\) を加算
  • BIT1 の l 番目に x を加算
  • BIT1 の r+1 番目に -x を加算

和の取得

  • sum(BIT0,i) + sum(BIT1, i)･i

BIT0 と BIT1の役割

BIT1 は、\(l \leq i \leq r\) の時の

  • sum'(i) = sum(i) + \(x\cdot (i-l+1) \)
    = sum(i) + \(x i\) – \(x (l-1)\)

という式のうちの、「\(x i\)」の部分を計算するのに対応しています。\(l \leq i \leq r\) 以外の時は、BIT1 が合計値の計算で使われる値は0になるはずです。

BIT0 はそれ以外の増加分や減少分を計算するのに使われています。

本当にそうなるのか、 i の値で場合分けして確かめてみると良いでしょう。

実装例

add のインターフェースとしては半開区間を採用していますが、内部では解説通り閉区間で動作しています。

/* BIT: RAQ対応BIT
    初期値は a_1 = a_2 = ... = a_n = 0
    ・add(l,r,x): [l,r) に x を加算する
    ・sum(i): a_1 + a_2 + ... + a_i を計算する
    計算量は全て O(logn)
*/
template <typename T>
struct BIT {
    int n;             // 要素数
    vector<T> bit[2];  // データの格納先
    BIT(int n_) { init(n_); }
    void init(int n_) {
        n = n_ + 1;
        for (int p = 0; p < 2; p++) bit[p].assign(n, 0);
    }

    void add_sub(int p, int i, T x) {
        for (int idx = i; idx < n; idx += (idx & -idx)) {
            bit[p][idx] += x;
        }
    }
    void add(int l, int r, T x) {  // [l,r) に加算
        add_sub(0, l, -x * (l - 1));
        add_sub(0, r, x * (r - 1));
        add_sub(1, l, x);
        add_sub(1, r, -x);
    }

    T sum_sub(int p, int i) {
        T s(0);
        for (int idx = i; idx > 0; idx -= (idx & -idx)) {
            s += bit[p][idx];
        }
        return s;
    }
    T sum(int i) { return sum_sub(0, i) + sum_sub(1, i) * i; }
};

BIT の応用

任意の区間和の取得

[l, r) の区間和は「[1, r)の区間和 – [1, l)の区間和」 で計算できることを利用すると、任意の区間の和を \(O(log n)\) で計算することが可能です。

// [l,r) の区間和を取得
T query(int l, int r) { return sum(r - 1) - sum(l - 1); }

BIT上の二分探索

\(a_1 + a_2 + … + a_x >= w\) となるような最小の x を求めることを考えます。

ナイーブにやると \(a_1 + a_2 + … + a_i\) の計算結果を二分探索して \(O((logn)^2)\) 程度かかりますが、BIT 上で二分探索を行うようにすると、\(O(log(n))\) で計算可能です。

イメージとしては、上から順番に必要な区間を決定していく感じです。

\(a_1 + a_2 + … + a_x >= w\) となるような最小の x が5 の時

区間の長さは一段下に下るごとに半分になるので、以下のように実装できます。

int lower_bound(T w) { // a_1 + a_2 + ... + a_x >= w となるような最小の x を求める(ただし a_i >= 0)
    if (w <= 0) {
        return 0;
    } else {
        int x = 0, r = 1;
        while (r < n) r = r << 1;
        for (int len = r; len > 0; len = len >> 1) { // 長さlenは1段下るごとに半分に
            if (x + len < n && bit[x + len] < w) { // 採用するとき
                w -= bit[x + len];
                x += len;
            }
        }
        return x + 1;
    }
}

転倒数(反転数)の計算

数列 \(a_1, a_2, a_3, \cdots, a_n\) が与えられた時に、

  • i < j かつ \(a_i > a_j\) となるペアの数

のことを「転倒数」とか「反転数」などと言い、バブルソートの交換回数と等しくなります。

バブルソートを行いつつカウントする場合は \(O(n^2)\) かかりますが、BIT を用いることで以下のアルゴリズムで \(O(n long n)\) の計算量で求めることができます。

  1. j=0 から n-1 まで以下を繰り返す
    1. j-sum(a[j])を答えに加える
    2. add(a[j],1) をする

sum(a[j])は i<j における a[i]<= a[j] となる数なので、 j-sum(a[j]) で j を固定したときの転倒数が求まります。

集合を管理して「 w 番目に小さい要素」を高速に取得

BITとBIT上での二分探索を活用すると、集合を管理して、

  • a が何番目に小さいか
  • w 番目に小さい要素 a は何か

というのを以下のように \(O(log n)\) で高速に取得することが可能です。

  • add(a,1): 集合への要素 a の追加(a 番目を 1 にする)
  • add(a,-1): 集合への要素 a の削除(a 番目を 1 から 0 にする)
  • sum(a): a が何番目に小さいか
  • lower_bound(w): w 番目に小さい要素 a は何か

値の範囲が N までとした時、消費メモリは \(O(N)\), 計算量はそれぞれ \(O(logN)\) だけかかることになります。

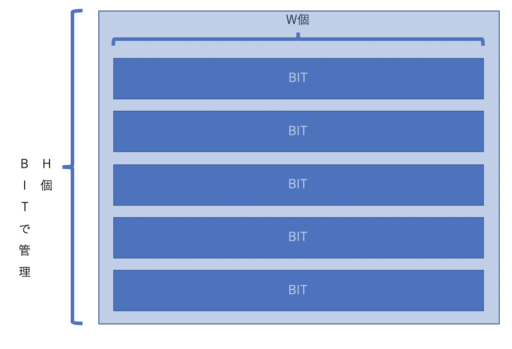
二次元のBIT

\(H \times W\) なる二次元の BIT に拡張することができます。

以下のように、要素数 W の BIT を 縦にH 個並べて、それらをBIT で管理します。

  • 加算：座標 (h,w) に x を加算する
  • 区間和取得：1≦i≦h かつ 1≦j≦w の範囲の合計値を求める

などの各操作の計算量は \(O(log W \times log H)\) となります。また、任意の区間の和は、2次元累積和的な考え方で取得することができます。

/* BIT2D:
    初期値は全て 0
    ・add(h,w,x): (h,w) に x を加算する
    ・sum(h,w): 1≦i≦h かつ 1≦j≦w の範囲の合計値を求める
    ・query(h1,w1,h2,w2): h1≦i<h2 かつ w1≦j<w2 の範囲の合計値を求める(1-indexed)
    計算量は全て O(logW * logH)
*/
template <typename T>
struct BIT2D {
    int H, W;
    vector<vector<T>> bit;  // データの格納先
    BIT2D(int H_, int W_) { init(H_, W_); }
    void init(int H_, int W_) {
        H = H_ + 1;
        W = W_ + 1;
        bit.assign(H, vector<T>(W, 0));
    }

    void add(int h, int w, T x) {
        for (int i = h; i < H; i += (i & -i)) {
            for (int j = w; j < W; j += (j & -j)) {
                bit[i][j] += x;
            }
        }
    }
    // 1≦i≦h かつ 1≦j≦w
    T sum(int h, int w) {
        T s(0);
        for (int i = h; i > 0; i -= (i & -i)) {
            for (int j = w; j > 0; j -= (j & -j)) {
                s += bit[i][j];
            }
        }
        return s;
    }

    // h1≦i<h2 かつ w1≦j<w2
    T query(int h1, int w1, int h2, int w2) {
        return sum(h2 - 1, w2 - 1) - sum(h2 - 1, w1 - 1) - sum(h1 - 1, w2 - 1) + sum(h1 - 1, w1 - 1);
    }
};

練習問題

基本

区間加算

転倒数

BIT での二分探索

二次元BIT

データ構造転倒数,二次元BIT,BIT,区間和,競プロ,二分探索,セグメント木,区間,データ構造,RAQ,RSQ