セグメント木を徹底解説！0から遅延評価やモノイドまで
セグメント木とは
セグメント木とは、完全二分木（全ての葉の深さが等しい木）によって実装された、区間を扱うのに適したデータ構造のことです。
区間に対する操作を対数時間 O(log n) で行えることが特徴で、競技プログラミングなどで頻出となっています。
セグメント木でできること
セグメント木は、区間に対する操作やクエリを行うことができます。
特に、
- 区間上の値を更新する
- 任意の区間上の最小値や合計値などを取得する
などが対数時間でそれぞれ行えるのが強みです。
区間上の合計値などは、累積和などを使えば前処理 O(N) ・クエリ O(1) で取得することもできます。しかし、区間上の値の更新と、合計値の取得が入り乱れるような時は、セグメント木の方が有効になることが多いです。
以下では説明のために、区間上の最小値 Range Minimam Query(RMQ) を扱うセグメント木を例として説明します。
セグメント木の気持ち
実装をする前に、どのようにしてセグメント木を実現するのかを見ていきましょう。
セグメント木では、完全二分木のそれぞれのノードが、一つの区間を表現しています。
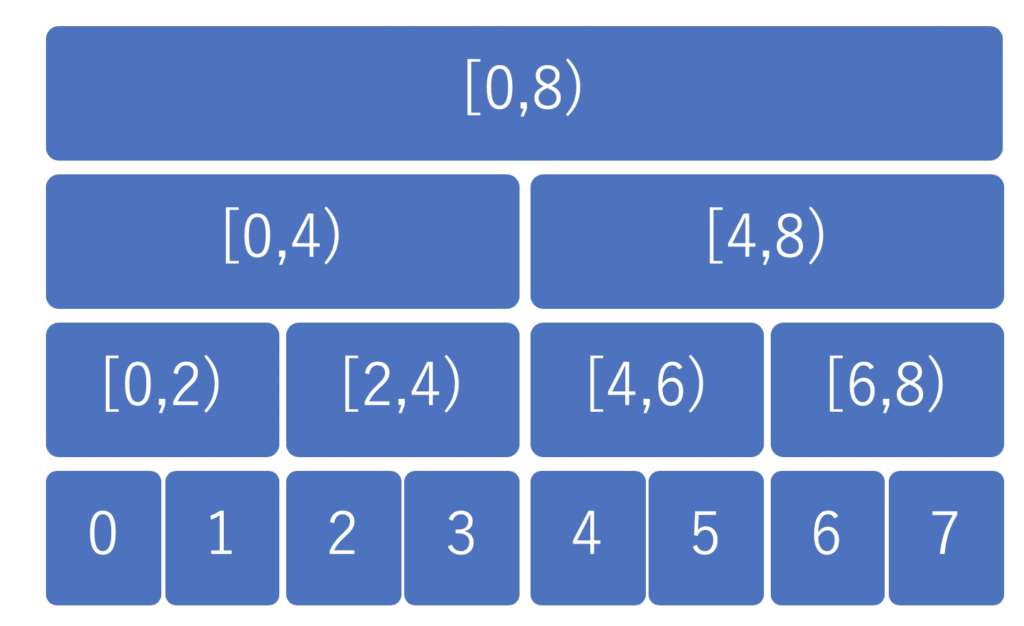
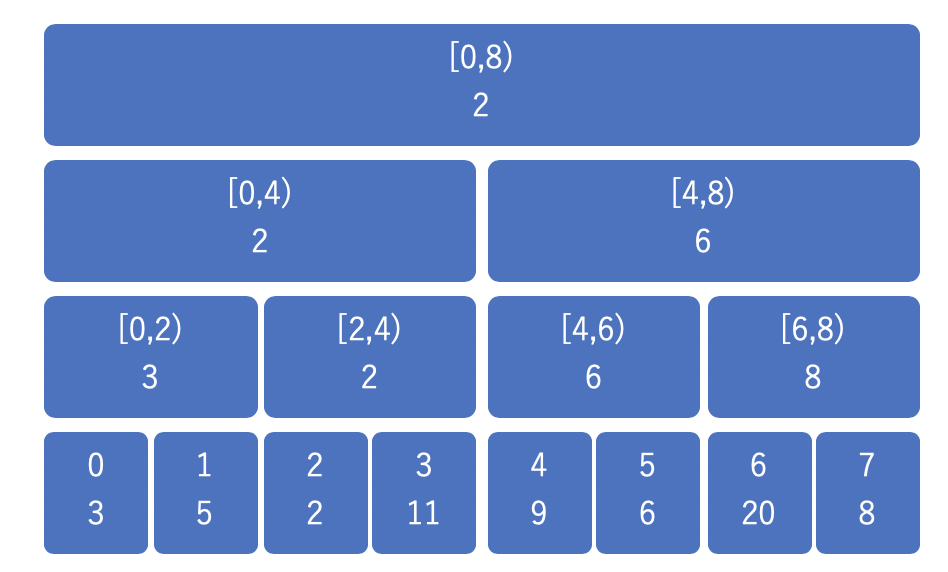
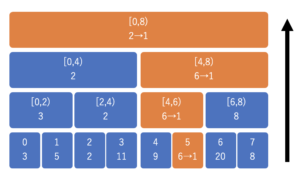
数列 \(a = \{3, 5, 2, 11, 9, 6, 20, 8\}\) についての RMQ を考えてみると、以下のように区間上の最小値をそれぞれのノードが持つことになります。
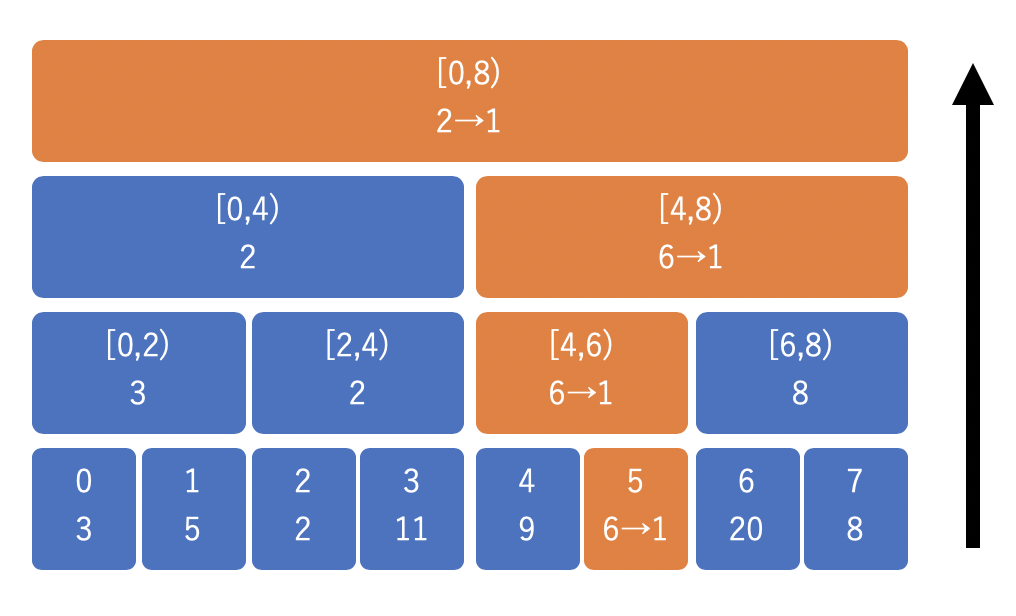
値を更新する時は、子ノードから親ノードへと辿りながら更新して行きます。下から上へと区間で受け止めるイメージです。
以下は 5 番目の値を 6 から 1 へと変更する時の様子です。
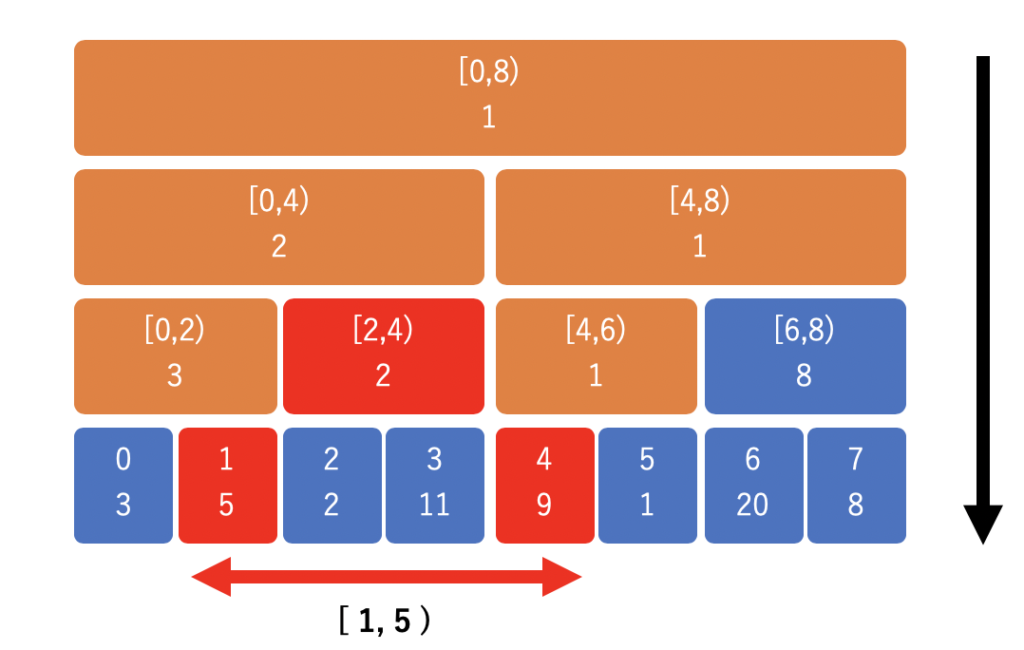
ある区間での最小値を知りたいときは、親ノードから子ノードへと辿りながら値を確認していきます。こちらは上から下へと区間で受け止めるイメージです。
以下は 区間 [1,5) の最小値を取得する時の様子です。[1, 5) に含まれる赤い区間を探して、その中の最小値を取得すればよいです。
値の更新・最小値の取得はともに木の高さに比例した計算量となります。ゆえに計算量が O(log n) になるのです。
セグメント木の実装（RMQ)
先程の方針を元にセグメント木を実装していきましょう。以下では n 個の数列に対する RMQ を実装することを考えます。
基本となるのは完全二分木
完全二分木を元にセグメント木を実装していきます。完全二分木は配列を用いて表現することができるので詳しく見ていきましょう。
葉のノード数
完全二分木は、全ての葉の深さが等しいものでした。つまり、木の深さを決めてしまうと葉の数も一意に定まってしまいます。
葉の数は必ず \(2^x\) の形をしているので、実際にセグメント木を用いる際は、余分な部分は0や大きな数などで埋めておく必要があります。
以下では数列のサイズ n は必要があれば \(2^x\) の形に水増ししたものとします。
全体のノード数
葉は n 個の数列に対応するので、全体としては 2n-1 個のノードで表すことができます。配列の全体のサイズは 2n-1 です。
以下では dat[2*n-1] というような配列で表すことにします。
親から子へのアクセス
配列の i 番目が表すノード dat[i] の子は、以下のように簡単にアクセスすることができます。
- 左の子：
dat[2*i+1] - 右の子：
dat[2*i+2]
子から親へのアクセス
配列の i 番目が表すノードについて、親へのアクセスも以下のように簡単にできます。
- 親：
dat[(i-1)/2]
値の更新
値の更新時は、更新したい点から親へとたどりながら、最小値を更新していきます。
void update(int i, int x) { // i: 更新したい数列の位置 x: 更新する値
i += n - 1; // i番目は、配列上では n-1+i 番目に格納されている
dat[i] = x; // 葉の更新
while (i > 0) { // 親を辿りながら更新していく
i = (i - 1) / 2; // parent
dat[i] = min(dat[i * 2 + 1], dat[i * 2 + 2]);
}
}
最小値の取得
最小値の取得は、親から子へとたどっていき、区間に収まるものを見つけます。
半開区間で実装するようにすると分かりやすいでしょう。
int query(int a, int b) { return query_sub(a, b, 0, 0, n); } // [a,b)の最小値を取得する
int query_sub(int a, int b, int k, int l, int r) {
// k:現在見ているノードの位置 [l,r):dat[k]が表している区間
if (r <= a || b <= l) { // 範囲外なら考えない
return INF;
} else if (a <= l && r <= b) { // 範囲内なので自身の値を返す
return dat[k];
} else { // 一部区間が被る時
int vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
int vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return min(vl, vr);
}
}
C++での実装のまとめ
構造体を利用して、RMQ のセグメント木を実装すると以下のようになります。
毎回 int 型とは限らないので、テンプレートを使って型が違うときにも対応できるようにすると良いでしょう。
/* RMQ：[0,n-1] について、区間ごとの最小値を管理する構造体
update(i,x): i 番目の要素を x に更新。O(log(n))
query(a,b): [a,b) での最小の要素を取得。O(log(n))
*/
template <typename T>
struct RMQ {
const T INF = numeric_limits<T>::max();
int n; // 葉の数
vector<T> dat; // 完全二分木の配列
RMQ(int n_) : n(), dat(n_ * 4, INF) { // 葉の数は 2^x の形
int x = 1;
while (n_ > x) {
x *= 2;
}
n = x;
}
void update(int i, T x) {
i += n - 1;
dat[i] = x;
while (i > 0) {
i = (i - 1) / 2; // parent
dat[i] = min(dat[i * 2 + 1], dat[i * 2 + 2]);
}
}
// the minimum element of [a,b)
T query(int a, int b) { return query_sub(a, b, 0, 0, n); }
T query_sub(int a, int b, int k, int l, int r) {
if (r <= a || b <= l) {
return INF;
} else if (a <= l && r <= b) {
return dat[k];
} else {
T vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
T vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return min(vl, vr);
}
}
};
遅延評価セグメント木（例:RMQ・RUQ)
- 区間更新：[a, b) の値を x に更新する
- 区間加算：[a, b) の値に x を加算する
などの操作は、さきほどまでのセグメント木では一点の更新を n 回行うことになるので O(n log n) だけかかってしまいますが、これを O(log n) でできるように改良したのが遅延評価セグメント木です。
以下では例として、 RMQ に加えて区間更新を行う Range Updated Query(RUQ) を考えてみましょう。
遅延評価セグメント木の気持ち
普通のセグメント木の一点更新では、更新するべきノードを一気に更新してしまいました。この更新を必要があるときまで遅らせるのが遅延評価セグメント木です。
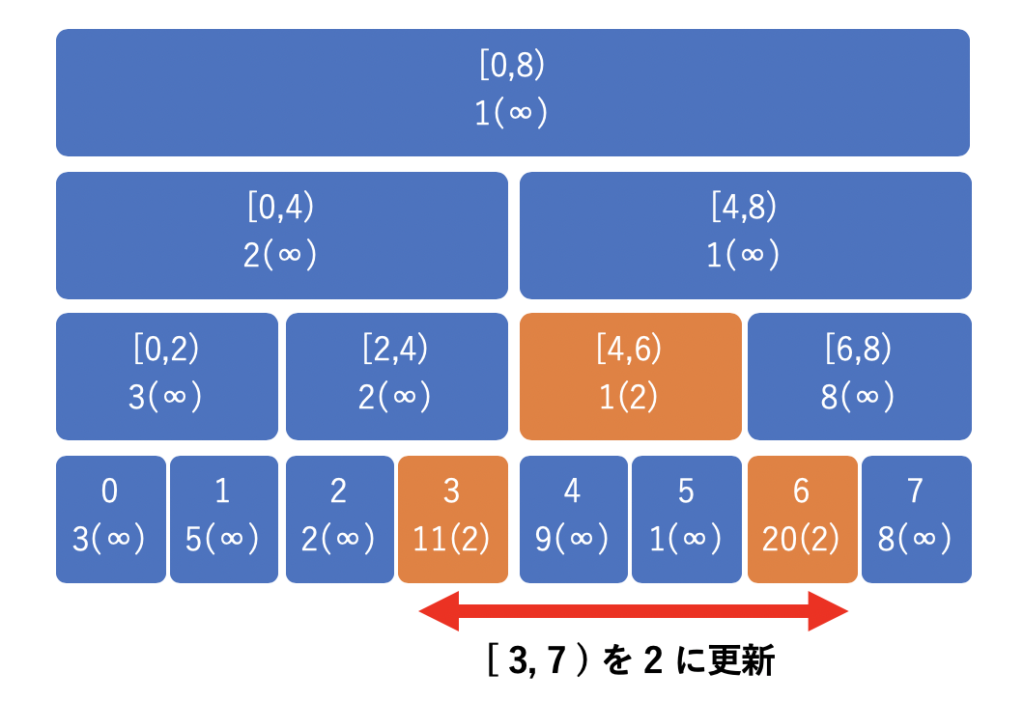
具体例で見ていきましょう。以下のようなセグメント木上で、[3,7) の区間の値を 2 に更新する時を考えてみます。
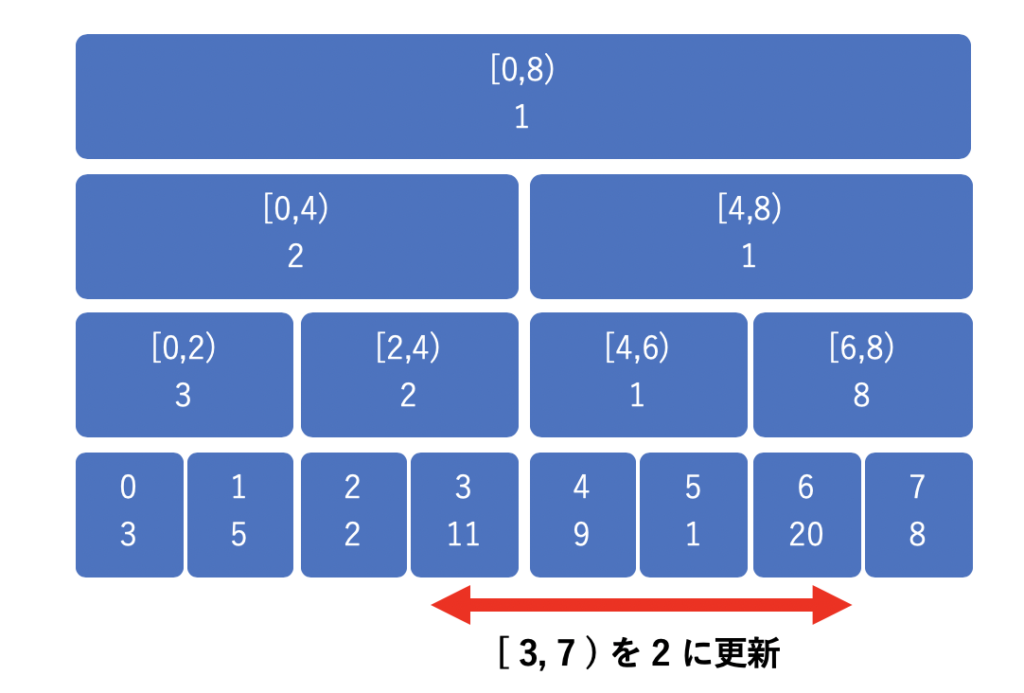
通常のセグメント木の更新では、以下のようにたくさんのノードを更新しなくてはなりません。
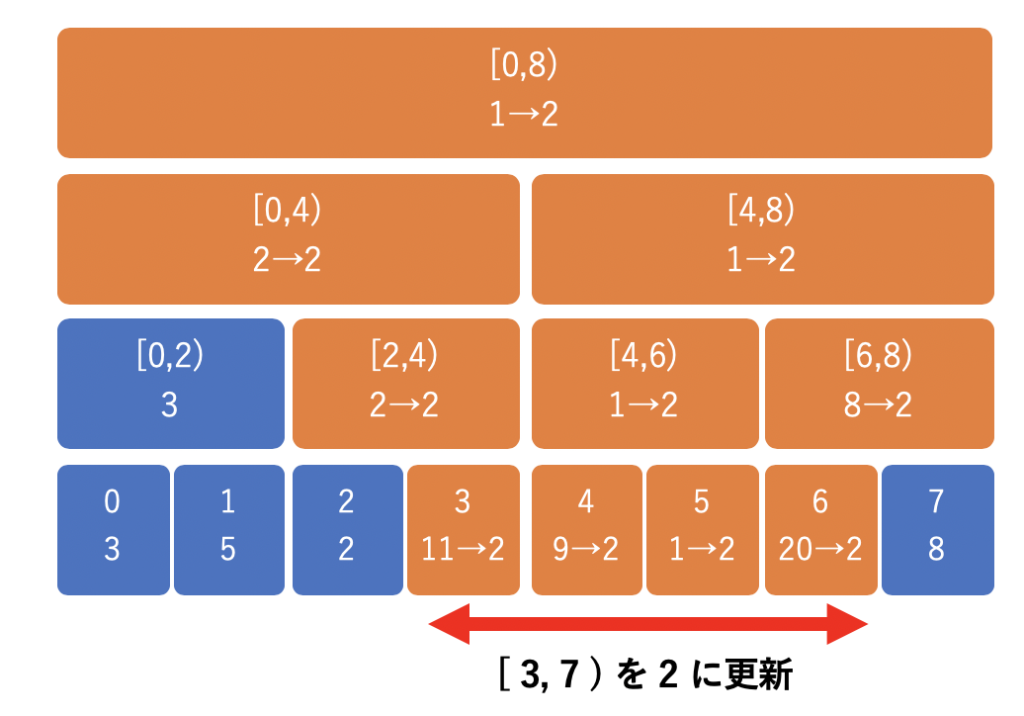
そこで、遅延セグメント木では、後で更新するために以下のように更新内容を別の完全二分木に保存しておきます。これだけなら木の高さに応じた分しか計算時間がかかりません。
後回しにした更新は、必要に迫られた際に行えば良いです。つまり、クエリでそのノードの最小値が必要になった際や二回目の更新を行う際に遅延評価を行いましょう。
以下は [1,5) の最小値を求める際の途中の様子です。現在[4,6) にいて、これから 4 番目の数列が格納されている場所を確認するところです。
複雑ですが、ここでは雰囲気を掴んでもらえれば大丈夫です。後で具体的なコードを確認しましょう。
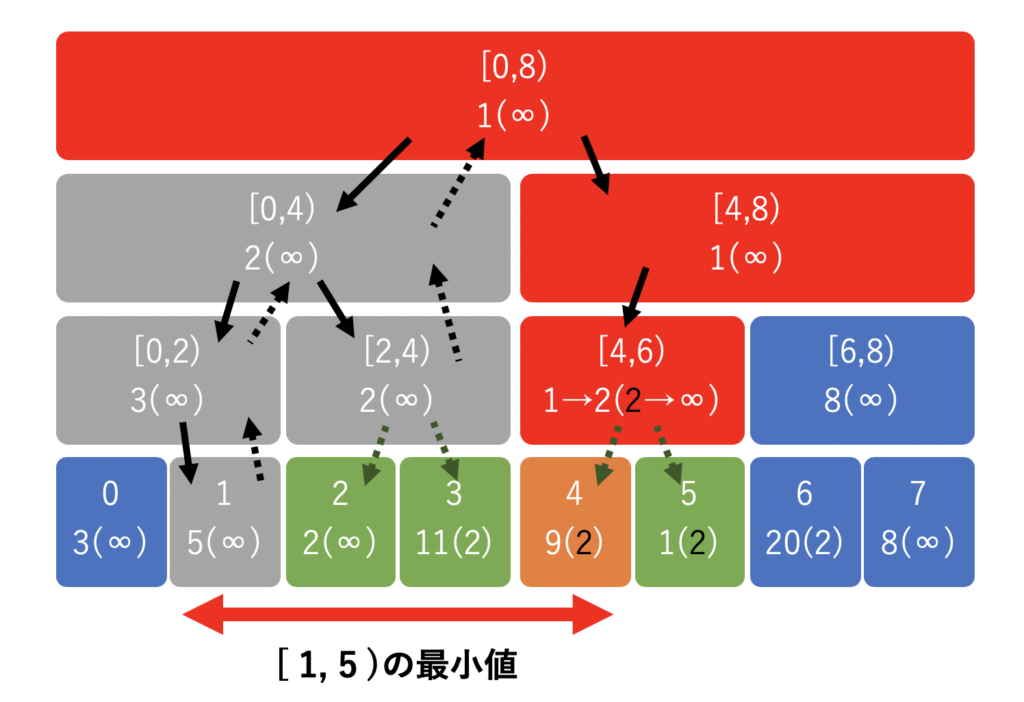
- 灰色：もう更新と最小値の確認の終わったノード
- 赤色：まだ確認途中のノード
- 橙色：これから確認するノード
- 緑色：親から、値(∞ or 2)を伝搬されたノード
以上のように最小値の取得を行うと、遅延評価ではないセグメント木に比べて値の遅延伝搬により計算は増えます。しかし、全体的にみれば O(log n) で最小値の取得と遅延伝搬の両方を行うことができるのです。
遅延評価セグメント木の実装
基本は普通のセグメント木と同じ
初期化や最小値の取得の方法などは、普通のセグメント木と大きく変わることはありません。
さきほどのセグメント木の実装に、遅延評価のコードをいくつか加えれば作ることができます。
遅延評価
遅延評価を行う際は、保持していた値を子に伝搬し、自身の値を更新します。
今回はRUQなので、値を上書きしてしまいますが、「区間に対して x を加算する」ような場合は値を加えることになります（詳しくはセグメント木の抽象化をする際に確認して下さい）。
void eval(int k) { // 配列のk番目を更新
if (lazy[k] == INF) return; // 更新するものが無ければ終了
if (k < n - 1) { // 葉でなければ子に伝搬
lazy[k * 2 + 1] = lazy[k];
lazy[k * 2 + 2] = lazy[k];
}
// 自身を更新
dat[k] = lazy[k];
lazy[k] = INF;
}
最小値の取得
最小値の取得のアルゴリズムはほとんど変わりありませんが、遅らせた更新を行っておく必要があります。
これにより自身は本来の値になり、子へも更新の情報が伝搬されていきます。
int query_sub(int a, int b, int k, int l, int r) {
eval(k); // ここが追加！
if (r <= a || b <= l) { // 完全に外側の時
return INF;
} else if (a <= l && r <= b) { // 完全に内側の時
return dat[k];
} else { // 一部区間が被る時
int vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
int vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return min(vl, vr);
}
}
int query(int a, int b) { return query_sub(a, b, 0, 0, n); }
区間の更新
区間の更新を行う際は、最小値の取得の際に利用したのと同様のアルゴリズムを用いることができます。
遅延評価用の配列 lazy に更新するための値を入れる必要があるのですが、更新したい区間に完全に含まれる場所のみについて行えば良いです。
はじめに遅延評価 eval を実行しておかないと、前の区間更新の際に入れていた値が消えてしまうので注意しましょう。
void update(int a, int b, int x, int k, int l, int r) {
eval(k);
if (a <= l && r <= b) { // 完全に内側の時
lazy[k] = x;
eval(k);
} else if (a < r && l < b) { // 一部区間が被る時
update(a, b, x, k * 2 + 1, l, (l + r) / 2); // 左の子
update(a, b, x, k * 2 + 2, (l + r) / 2, r); // 右の子
dat[k] = min(dat[k * 2 + 1], dat[k * 2 + 2]);
}
}
void update(int a, int b, int x) { update(a, b, x, 0, 0, n); }
C++での実装のまとめ
構造体を利用して、区間更新型の RMQ のセグメント木を実装すると以下のようになります。
/* RMQ：[0,n-1] について、区間ごとの最小値を管理する構造体
update(a,b,x): 区間[a,b) の要素を x に更新。O(log(n))
query(a,b): [a,b) での最小の要素を取得。O(log(n))
*/
template <typename T>
struct RMQ {
const T INF = numeric_limits<T>::max();
int n;
vector<T> dat, lazy;
RMQ(int n_) : n(), dat(n_ * 4, INF), lazy(n_ * 4, INF) {
int x = 1;
while (n_ > x) x *= 2;
n = x;
}
/* lazy eval */
void eval(int k) {
if (lazy[k] == INF) return; // 更新するものが無ければ終了
if (k < n - 1) { // 葉でなければ子に伝搬
lazy[k * 2 + 1] = lazy[k];
lazy[k * 2 + 2] = lazy[k];
}
// 自身を更新
dat[k] = lazy[k];
lazy[k] = INF;
}
void update(int a, int b, T x, int k, int l, int r) {
eval(k);
if (a <= l && r <= b) { // 完全に内側の時
lazy[k] = x;
eval(k);
} else if (a < r && l < b) { // 一部区間が被る時
update(a, b, x, k * 2 + 1, l, (l + r) / 2); // 左の子
update(a, b, x, k * 2 + 2, (l + r) / 2, r); // 右の子
dat[k] = min(dat[k * 2 + 1], dat[k * 2 + 2]);
}
}
void update(int a, int b, T x) { update(a, b, x, 0, 0, n); }
T query_sub(int a, int b, int k, int l, int r) {
eval(k);
if (r <= a || b <= l) { // 完全に外側の時
return INF;
} else if (a <= l && r <= b) { // 完全に内側の時
return dat[k];
} else { // 一部区間が被る時
T vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
T vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return min(vl, vr);
}
}
T query(int a, int b) { return query_sub(a, b, 0, 0, n); }
/* debug */
inline T operator[](int a) { return query(a, a + 1); }
void print() {
for (int i = 0; i < 2 * n - 1; ++i) {
cout << (*this)[i];
if (i != n) cout << ",";
}
cout << endl;
}
};
セグメント木の応用テクニック
木の構築をまとめてO(n)で行う
値の更新には O(log n) だけかかるため、 n 個の更新を行おうとすると O(nlog n) だけかかります。
しかし、はじめに n 個の要素を葉にセットしてから、後で同時に更新することで、これを O(n) に抑えることが可能です。
ただし、これでは途中の状態での区間の最小値などは取得できないので注意してください。
void set(int i, T x) { dat[i + n - 1] = x; }
void build() {
for (int k = n - 2; k >= 0; k--){
dat[k] = min(dat[2 * k + 1], dat[2 * k + 2]);
}
}
セグメントツリー上での二分探索を高速に
RMQ では以下のようなクエリに答えたい場合があります。
- [a,b) で x以下の要素を持つ最右位置はどこか
- [a,b) で x以下の要素を持つ最左位置はどこか
今までに実装したセグメント木のクエリを使って、普通に二分探索を行うと \(O((log n)^2)\) の計算量になります。
しかし、以下のようにセグメント木の構造を利用して探索することで、 \(O(log n)\) にまで減らすことができるのです。
最右位置を知りたい場合は右の子ノードから探索するようにして、答えが見つかったら終了すれば良いです。
int find_rightest(int a, int b, T x) { return find_rightest_sub(a, b, x, 0, 0, n); }
int find_rightest_sub(int a, int b, T x, int k, int l, int r) {
if (dat[k] > x || r <= a || b <= l) { // 自分の値がxより大きい or [a,b)が[l,r)の範囲外ならreturn a-1
return a - 1;
} else if (k >= n - 1) { // 自分が葉ならその位置をreturn
return (k - (n - 1));
} else {
int vr = find_rightest_sub(a, b, x, 2 * k + 2, (l + r) / 2, r);
if (vr != a - 1) { // 右の部分木を見て a-1 以外ならreturn
return vr;
} else { // 左の部分木を見て値をreturn
return find_rightest_sub(a, b, x, 2 * k + 1, l, (l + r) / 2);
}
}
}
find_rightest_subのはじめの一行目に、遅延評価用のeval関数を差し込むと、遅延評価セグメント木でも二分探索をすることができます。
セグメント木によるRMQのまとめ
上述のものを全て組み合わせて、以下の機能を盛り込んだセグメント木を実装します。
- set(i, x), build(): i番目の要素をxにセットし、buildでまとめてセグ木を構築する
- update(a,b,x): 区間 [a,b) の要素を x に更新
- query(a,b): 区間 [a,b) での最小の要素を取得
- find_rightest(a,b,x): [a,b) で x以下の要素を持つ最右位置を求める
- find_leftest(a,b,x): [a,b) で x以下の要素を持つ最左位置を求める
これだけ機能があれば、区間更新型のRMQで不自由はしないでしょう。他のセグメント木も少しコードを変更するだけで作ることができます。
/* RMQ：[0,n-1] について、区間ごとの最小値を管理する構造体
set(int i, T x), build(): i番目の要素をxにセット。まとめてセグ木を構築する。O(n)
update(i,x): i 番目の要素を x に更新。O(log(n))
query(a,b): [a,b) での最小の要素を取得。O(log(n))
find_rightest(a,b,x): [a,b) で x以下の要素を持つ最右位置を求める。O(log(n))
find_leftest(a,b,x): [a,b) で x以下の要素を持つ最左位置を求める。O(log(n))
*/
template <typename T>
struct RMQ {
const T e = numeric_limits<T>::max();
function<T(T, T)> fx = [](T x1, T x2) -> T { return min(x1, x2); };
int n;
vector<T> dat;
RMQ(int n_) : n(), dat(n_ * 4, e) {
int x = 1;
while (n_ > x) {
x *= 2;
}
n = x;
}
void set(int i, T x) { dat[i + n - 1] = x; }
void build() {
for (int k = n - 2; k >= 0; k--) dat[k] = fx(dat[2 * k + 1], dat[2 * k + 2]);
}
void update(int i, T x) {
i += n - 1;
dat[i] = x;
while (i > 0) {
i = (i - 1) / 2; // parent
dat[i] = fx(dat[i * 2 + 1], dat[i * 2 + 2]);
}
}
// the minimum element of [a,b)
T query(int a, int b) { return query_sub(a, b, 0, 0, n); }
T query_sub(int a, int b, int k, int l, int r) {
if (r <= a || b <= l) {
return e;
} else if (a <= l && r <= b) {
return dat[k];
} else {
T vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
T vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return fx(vl, vr);
}
}
int find_rightest(int a, int b, T x) { return find_rightest_sub(a, b, x, 0, 0, n); }
int find_leftest(int a, int b, T x) { return find_leftest_sub(a, b, x, 0, 0, n); }
int find_rightest_sub(int a, int b, T x, int k, int l, int r) {
if (dat[k] > x || r <= a || b <= l) { // 自分の値がxより大きい or [a,b)が[l,r)の範囲外ならreturn a-1
return a - 1;
} else if (k >= n - 1) { // 自分が葉ならその位置をreturn
return (k - (n - 1));
} else {
int vr = find_rightest_sub(a, b, x, 2 * k + 2, (l + r) / 2, r);
if (vr != a - 1) { // 右の部分木を見て a-1 以外ならreturn
return vr;
} else { // 左の部分木を見て値をreturn
return find_rightest_sub(a, b, x, 2 * k + 1, l, (l + r) / 2);
}
}
}
int find_leftest_sub(int a, int b, T x, int k, int l, int r) {
if (dat[k] > x || r <= a || b <= l) { // 自分の値がxより大きい or [a,b)が[l,r)の範囲外ならreturn b
return b;
} else if (k >= n - 1) { // 自分が葉ならその位置をreturn
return (k - (n - 1));
} else {
int vl = find_leftest_sub(a, b, x, 2 * k + 1, l, (l + r) / 2);
if (vl != b) { // 左の部分木を見て b 以外ならreturn
return vl;
} else { // 右の部分木を見て値をreturn
return find_leftest_sub(a, b, x, 2 * k + 2, (l + r) / 2, r);
}
}
}
};
※2020/04/13 型を一部修正
セグメント木をより深く理解する
セグメント木でできることは、一点更新型や区間更新(RUQ)型のRMQだけではありません。以下のように更新の方法やクエリで知りたい内容によって、様々なバリエーションがあります。
- updateの方法：一点更新・一点加算・区間更新・区間加算など
- queryの内容：区間の最小値・区間の最大値・区間の合計値など
さきほどまでRMQの遅延評価セグメント木で考えていたものは、
- updateの方法：区間更新
- queryの内容：区間の最小値
となるものでした。
それではこれらを一般化・抽象化すると、どのような物に対してセグメント木を利用することができると言えるのでしょうか？
セグメント木に載せられるのはモノイド
セグメント木は様々なものに応用可能と言いましたが、（遅延評価でない場合は）「モノイド」に対して使用できることが知られています。
モノイドとは、集合 X と 、X 上の二項演算 \(•\): X × X → X について
- 結合則：X の任意の元 \(a,b,c\) について、\(a•(b•c) = (a•b)•c\)
- 単位元 e の存在：Mの任意の元 a について、\(e•a = a•e = a\) を満たす X の元 e が存在する
が同時に成り立つようなものを言います。
セグメント木のクエリで得られる値は、区間[a,b) の全ての要素に対して \(•\) を作用させた値となります。つまり、\(a•(a+1)•(a+2)•…•(b-1)\) となります。
実際に先程までの一点更新型のRMQでは、「集合X：int型の整数全体」、「二項演算 •：min(a,b)」などとすると
- 結合則：\(min(a,min(b,c)) = min(min(a,b),c)\)
- 単位元 e の存在：int型の最大値 INF
が同時に成り立つのでこれはモノイドです。
また、クエリで得られる値は、区間[a,b) の全てに対して min を作用させた値となります。つまり、\(\min(a,a+1,a+2,a+3,…,b-1)\) のことです。
補足：「二項演算 \(•\): X × X → X」の意味
少し数学的表現が増えて、分かりにくいので説明しておきます。
まず、「X ×X」の意味について。
一つ目の X の元 x と、2つ目の X の元 x’の組として (x,x’)が作れるとします。このような組として考えられるものを全て集めて集合にしたものを 「X ×X」と表現し、これを XとXの直積 と言います。
また、「X × X → X」は、集合「X × X」から「X」への写像であることを表しています。「二項演算 \(•\) は、X × X の元 (x,x’) を受け取って、Xの元を返す」ということをここでは述べているのです。
二項演算\(•\) の定義域が「X × X」で、値域が「X」であることを表していると言い換えても良いです。
遅延評価セグメント木に載せられるのは作用付きモノイド
遅延評価セグメント木に載せられるのは、モノイドに作用と呼ばれるものを付け加えた「作用付きモノイド」です。
先程のモノイドの定義に、集合 M と 二項演算 \(×\)：M × M → M、二項演算 \(*\)：X × M → X を加えて、
- X と二項演算 \(•\) はモノイド
- M と二項演算 \(×\) はモノイド
- Mの単位元\(e_m\)について、\(x*e_m = x\)
- \((x1•x2)*m = (x1*m)•(x2*m)\)
- \((x*m1)*m2 = x*(m1×m2)\)
が成り立つものです。右からMを作用させるので、右作用などと言います。（同様に左作用もあります。）
遅延評価セグメント木では、Xがセグメント木のデータ、作用素Mが遅延伝搬させる値に対応します。
実際に区間更新型のRMQでは、
- 集合X：int型の整数全体
- 集合M：int型の整数全体
- 二項演算 •：\(min(x1,x2)\)
- 二項演算 \(×\)：\(m1×m2=m2\) ただし m2 が INF のときは \(m1×m2=m1\)
- 二項演算 *：\(x*m = m\) ただし m が INF のときは \(x*m=x\)
とすることで、
- X と二項演算 min はモノイド(単位元は INF)
- M と二項演算 \(×\) はモノイド(単位元は INF)
- \(x*\)INF \(= x*e_m = x\)
- \(min(x1,x2)*m = m = min((x1*m),(x2*m))\) (mがINFでない)
- \(min(x1,x2)*m = min(x1,x2) = min((x1*m),(x2*m))\) (mがINF)
- \((x*m1)*m2 = m2 = x*(m1×m2)\) (m2がINFでない)
- \((x*m1)*m2 = m1 = x*(m1×m2)\) (m2がINFでm1はINFでない)
- \((x*m1)*m2 = x = x*(m1×m2)\) (m1,m2がINF)
となり条件を全て満たすことができます。
抽象化したセグメント木を実装する
任意のモノイドに対して、すぐにセグメント木を構築できるようにしてみましょう。
以下を引数に渡してセグメントツリーを構築します。
- fx: モノイドXでの二項演算
- ex: モノイドXでの単位元
関数自体を引数として渡す必要があるので、「ラムダ式」と呼ばれるものを利用します。C++での書き方が良くわからない方はこちらなどを参考にしてください。
/* SegTree<X>(n,fx,ex): モノイド(集合X, 二項演算fx, 単位元ex)についてサイズnで構築
set(int i, X x), build(): i番目の要素をxにセット。まとめてセグ木を構築する。O(n)
update(i,x): i 番目の要素を x に更新。O(log(n))
query(a,b): [a,b) 全てにfxを作用させた値を取得。O(log(n))
*/
template <typename X>
struct SegTree {
using FX = function<X(X, X)>; // X•X -> X となる関数の型
int n;
FX fx;
const X ex;
vector<X> dat;
SegTree(int n_, FX fx_, X ex_) : n(), fx(fx_), ex(ex_), dat(n_ * 4, ex_) {
int x = 1;
while (n_ > x) {
x *= 2;
}
n = x;
}
void set(int i, X x) { dat[i + n - 1] = x; }
void build() {
for (int k = n - 2; k >= 0; k--) dat[k] = fx(dat[2 * k + 1], dat[2 * k + 2]);
}
void update(int i, X x) {
i += n - 1;
dat[i] = x;
while (i > 0) {
i = (i - 1) / 2; // parent
dat[i] = fx(dat[i * 2 + 1], dat[i * 2 + 2]);
}
}
X query(int a, int b) { return query_sub(a, b, 0, 0, n); }
X query_sub(int a, int b, int k, int l, int r) {
if (r <= a || b <= l) {
return ex;
} else if (a <= l && r <= b) {
return dat[k];
} else {
X vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
X vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return fx(vl, vr);
}
}
};
一点更新型のRMQの場合は以下のようにすれば構築できます。
auto fx = [](int x1, int x2) -> int { return min(x1, x2); };
int ex = numeric_limits<int>::max();
SegTree<int> rmq(n, fx, ex);
抽象化した遅延評価セグメント木を実装する
こんどは任意の作用付きモノイドに対して、遅延評価セグメント木が構築できるようにしましょう。
以下を引数に渡してセグメント木を構築します。
- fx: X × X → X
- fa: X × M → X
- fm: M × M → M
- ex: モノイドXでの単位元
- em: モノイドMでの単位元
/* SegTreeLazy<X,M>(n,fx,fa,fm,ex,em): モノイド(集合X, 二項演算fx,fa,fm, 単位元ex,em)についてサイズnで構築
set(int i, X x), build(): i番目の要素をxにセット。まとめてセグ木を構築する。O(n)
update(i,x): i 番目の要素を x に更新。O(log(n))
query(a,b): [a,b) 全てにfxを作用させた値を取得。O(log(n))
*/
template <typename X, typename M>
struct SegTreeLazy {
using FX = function<X(X, X)>;
using FA = function<X(X, M)>;
using FM = function<M(M, M)>;
int n;
FX fx;
FA fa;
FM fm;
const X ex;
const M em;
vector<X> dat;
vector<M> lazy;
SegTreeLazy(int n_, FX fx_, FA fa_, FM fm_, X ex_, M em_)
: n(), fx(fx_), fa(fa_), fm(fm_), ex(ex_), em(em_), dat(n_ * 4, ex), lazy(n_ * 4, em) {
int x = 1;
while (n_ > x) x *= 2;
n = x;
}
void set(int i, X x) { dat[i + n - 1] = x; }
void build() {
for (int k = n - 2; k >= 0; k--) dat[k] = fx(dat[2 * k + 1], dat[2 * k + 2]);
}
/* lazy eval */
void eval(int k) {
if (lazy[k] == em) return; // 更新するものが無ければ終了
if (k < n - 1) { // 葉でなければ子に伝搬
lazy[k * 2 + 1] = fm(lazy[k * 2 + 1], lazy[k]);
lazy[k * 2 + 2] = fm(lazy[k * 2 + 2], lazy[k]);
}
// 自身を更新
dat[k] = fa(dat[k], lazy[k]);
lazy[k] = em;
}
void update(int a, int b, M x, int k, int l, int r) {
eval(k);
if (a <= l && r <= b) { // 完全に内側の時
lazy[k] = fm(lazy[k], x);
eval(k);
} else if (a < r && l < b) { // 一部区間が被る時
update(a, b, x, k * 2 + 1, l, (l + r) / 2); // 左の子
update(a, b, x, k * 2 + 2, (l + r) / 2, r); // 右の子
dat[k] = fx(dat[k * 2 + 1], dat[k * 2 + 2]);
}
}
void update(int a, int b, M x) { update(a, b, x, 0, 0, n); }
X query_sub(int a, int b, int k, int l, int r) {
eval(k);
if (r <= a || b <= l) { // 完全に外側の時
return ex;
} else if (a <= l && r <= b) { // 完全に内側の時
return dat[k];
} else { // 一部区間が被る時
X vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
X vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return fx(vl, vr);
}
}
X query(int a, int b) { return query_sub(a, b, 0, 0, n); }
};
区間更新型のRMQを構築するには以下のようにすれば良いです。
using X = int;
using M = int;
auto fx = [](X x1, X x2) -> X { return min(x1, x2); };
auto fa = [](X x, M m) -> X { return m; };
auto fm = [](M m1, M m2) -> M { return m2; };
int ex = numeric_limits<int>::max();
int em = numeric_limits<int>::max();
SegTreeLazy<X, M> rmq(n, fx, fa, fm, ex, em);
これは厳密には
- 二項演算 fm(\(×\))：\(m1×m2=m2\) ただし m2 が INF のときは \(m1×m2=m1\)
- 二項演算 fa(\(*\))：\(x*m = m \) ただし m が INF のときは \(x*m=x\)
が成立していませんが、updateメソッド内でMの単位元を右から作用させるときは何もしないようにしているので問題は生じません。
さらに応用：区間に比例した作用素
写像 \(p\) を \(p(m,n) := \overbrace{m*m*\cdots*m}^{n個}\)と定めると、
- X と二項演算 \(•\) はモノイド
- M と二項演算 \(×\) はモノイド
- Mの単位元 \(e_m\)について、\(x*e_m = x\)
- \((x1•x2)*p(m,n) = (x1*p(m,n/2))•(x2*p(m,n/2))\)
- \((x*m1)*m2 = x*(m1×m2)\)
が成立し、p が高速に計算できる場合、これも遅延評価セグメント木によって解くことができます。
ここでの n は区間の要素数に対応しています。つまり、区間の要素数に比例して作用素が影響する場合、遅延評価セグメント木が使えます。
/* SegTreeLazyProportional<X,M>(n,fx,fa,fm,fp,ex,em): モノイド(集合X, 二項演算fx,fa,fm,p 単位元ex,em)についてサイズnで構築
set(int i, X x), build(): i番目の要素をxにセット。まとめてセグ木を構築する。O(n)
update(i,x): i 番目の要素を x に更新。O(log(n))
query(a,b): [a,b) 全てにfxを作用させた値を取得。O(log(n))
*/
template <typename X, typename M>
struct SegTreeLazyProportional {
using FX = function<X(X, X)>;
using FA = function<X(X, M)>;
using FM = function<M(M, M)>;
using FP = function<M(M, int)>;
int n;
FX fx;
FA fa;
FM fm;
FP fp;
const X ex;
const M em;
vector<X> dat;
vector<M> lazy;
SegTreeLazyProportional(int n_, FX fx_, FA fa_, FM fm_, FP fp_, X ex_, M em_)
: n(), fx(fx_), fa(fa_), fm(fm_), fp(fp_), ex(ex_), em(em_), dat(n_ * 4, ex), lazy(n_ * 4, em) {
int x = 1;
while (n_ > x) x *= 2;
n = x;
}
void set(int i, X x) { dat[i + n - 1] = x; }
void build() {
for (int k = n - 2; k >= 0; k--) dat[k] = fx(dat[2 * k + 1], dat[2 * k + 2]);
}
/* lazy eval */
void eval(int k, int len) {
if (lazy[k] == em) return; // 更新するものが無ければ終了
if (k < n - 1) { // 葉でなければ子に伝搬
lazy[k * 2 + 1] = fm(lazy[k * 2 + 1], lazy[k]);
lazy[k * 2 + 2] = fm(lazy[k * 2 + 2], lazy[k]);
}
// 自身を更新
dat[k] = fa(dat[k], fp(lazy[k], len));
lazy[k] = em;
}
void update(int a, int b, M x, int k, int l, int r) {
eval(k, r - l);
if (a <= l && r <= b) { // 完全に内側の時
lazy[k] = fm(lazy[k], x);
eval(k, r - l);
} else if (a < r && l < b) { // 一部区間が被る時
update(a, b, x, k * 2 + 1, l, (l + r) / 2); // 左の子
update(a, b, x, k * 2 + 2, (l + r) / 2, r); // 右の子
dat[k] = fx(dat[k * 2 + 1], dat[k * 2 + 2]);
}
}
void update(int a, int b, M x) { update(a, b, x, 0, 0, n); }
X query_sub(int a, int b, int k, int l, int r) {
eval(k, r - l);
if (r <= a || b <= l) { // 完全に外側の時
return ex;
} else if (a <= l && r <= b) { // 完全に内側の時
return dat[k];
} else { // 一部区間が被る時
X vl = query_sub(a, b, k * 2 + 1, l, (l + r) / 2);
X vr = query_sub(a, b, k * 2 + 2, (l + r) / 2, r);
return fx(vl, vr);
}
}
X query(int a, int b) { return query_sub(a, b, 0, 0, n); }
};
具体的な応用先としては、区間和 Range Sum Query(RSQ) の問題などで使うことができます。
例えば、[1,3) の区間に a を加算したとすれば、その区間の区間和は a*2 だけ増えることになります。これは区間のサイズに比例して値が加算されるということです。
以下は区間加算 Range Add Query(RAQ) 型の RSQ に関するセグメント木です。
using X = long long;
using M = long long;
auto fx = [](X x1, X x2) -> X { return x1 + x2; };
auto fa = [](X x, M m) -> X { return x + m; };
auto fm = [](M m1, M m2) -> M { return m1 + m2; };
auto fp = [](M m, long long n) -> M { return m * n; };
long long ex = 0;
long long em = 0;
SegTreeLazyProportional<X, M> rmq(n, fx, fa, fm, fp, ex, em);
RMQのときの実装と同様に、RSQのときもセグメント木上での二分探索を行うことが可能です。その場合は「\(a_1 + a_2 + … + a_x >= w\) となるような最小の x 」を高速に求めることが可能です。
RSQ型の問題は、BIT(Binary Indexed Tree) を用いることでも解けます。BITはセグメントツリーの特殊系と捉える事もでき、高速に動作しますが、以上のようにセグメントツリーで代用も可能です。
練習問題
セグメント木
遅延評価セグメント木
- AOJ DSL_2_F RMQ and RUQ：区間更新(RUQ)のRMQ
- AOJ DSL_2_H RMQ and RAQ：区間加算(RAQ)のRMQ
- [AtCoder] ABC035 C – オセロ：区間加算・一点取得
- [AtCoder] ABC157 E – Simple String Queries（解説）：英小文字が出現したかどうかをbitで保持しましょう
セグメント木での二分探索
- [AtCoder] AGC 005 B – Minimum Sum：set でも解けます
- [AtCoder] ARC 033 C – データ構造：RSQでの二分探索で解けます。BITを利用しても良いです
- Codeforces Round #622 (Div. 2) C2. Skyscrapers (hard version)：普通のRMQ or RMQの二分探索を使う方法があります
区間に比例した作用素
- AOJ DSL_2_B RSQ：一点更新のRSQ。BITでもできます
- AOJ DSL_2_G RSQ and RAQ：区間加算(RAQ)のRSQ。区間加算対応BITでもできます