ベルマンフォード法による単一始点最短経路を求めるアルゴリズム

2020年3月7日グラフグラフ,競プロ,重み付きグラフ,ベルマンフォード法,単一始点最短経路,最短経路,負の閉路,負の辺

グラフにおける単一始点最短経路問題とは、始点を固定した時に、他のすべての頂点への最短経路を求める問題のことです。

ベルマンフォード法は、単一始点最短経路問題を解く時に利用され、

  • 負の辺が含まれているような場合でも適用可能
  • 負の閉路がグラフに含まれている際はそれを検出することができる

という利点があります。

アルゴリズム

ベルマンフォード法：

  1. 最短距離が更新されなくなるか、|V| 回目の更新が終わるまで以下を繰り返す
    • 全ての辺に対して、「d[v] = min{ d[u] + ( u から v への距離 ) }」という更新式を利用して最短距離を更新する
  2. |V-1| 回以内の更新で終了すれば負の閉路は存在しない。|V| 回まで更新が続けば負の閉路が存在する

※ 1. では、１回のループごとに１つの「最短距離が決まった頂点」を確定させていくイメージです。
※ |V| 回までとするのは、負の閉路がある場合は最短距離は更新の度に小さくなってしまい、更新が止まらなくなるからです。

計算量

  • \(O(|V|\times |E|)\)

全ての辺を確認して更新を行うのに \(O(|E|)\) だけかかり、それを高々 |V-1| 回行う必要があります。

C++の実装例

struct Edge {
    long long from;
    long long to;
    long long cost;
};
using Edges = vector<Edge>;
const long long INF = 1LL << 60;

/* bellman_ford(Es,s,t,dis)
    入力: 全ての辺Es, 頂点数V, 開始点 s, 最短経路を記録するdis
    出力: 負の閉路が存在するなら ture
    計算量：O(|E||V|)
    副作用：dis が書き換えられる
*/
bool bellman_ford(const Edges &Es, int V, int s, vector<long long> &dis) {
    dis.resize(V, INF);
    dis[s] = 0;
    int cnt = 0;
    while (cnt < V) {
        bool end = true;
        for (auto e : Es) {
            if (dis[e.from] != INF && dis[e.from] + e.cost < dis[e.to]) {
                dis[e.to] = dis[e.from] + e.cost;
                end = false;
            }
        }
        if (end) break;
        cnt++;
    }
    return (cnt == V);
}

アルゴリズムの考え方と正当性

基本となる式と考え方

頂点集合を V・辺の集合を E とした、グラフ G=(V,E) において、始点 s から 頂点 t への最短距離を d[t] と表すことにします。

ベルマンフォード法では、以下の式が成り立つことを利用します。

  • d[v] = min{d[u] + ( 辺e=(u,v) の距離 )}

つまり、辺e=(u,v) について考えると、頂点 v への最短経路はある頂点 u を経由した形で表現できるのです。

この式を利用して、最短距離を始点 s に近い頂点から順番に決定していくことができれば、すべての頂点に対して最短距離を求めることが可能です。

更新の順番は決まらない

もしグラフが、閉路の無い有向グラフ(DAG) であれば、左の頂点から順番に最短経路を決定できるので、\(O(E)\) 程度で実現可能です。

DAG なら左の頂点から決定できる

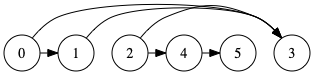
しかし、一般的なグラフでは閉路が存在する可能性があるのでうまくいきません。

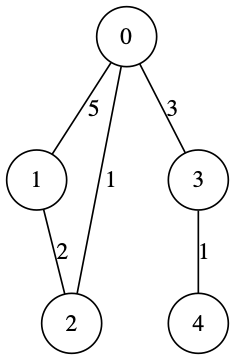
閉路が存在するのでどの頂点から順番に最短距離が求まるのか不明

そこでどうするかというと、

  • 全ての辺を確認して基本の式に基づいて最短距離を更新すると、どれかは分からないが少なくとも 1つの頂点への最短経路が定まる

という性質を用います。つまり、\(O(|E|)\) の更新を高々 |V-1| 回程度行えば、すべての頂点が更新されるのです。

具体例

具体例を通して、どのように更新されるのかの感覚を掴みましょう。s からの最短距離を更新していきます。

はじめの状態

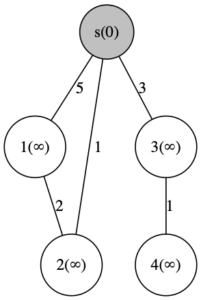
まずは、１回目の更新です。全ての辺を確認して、最短経路を「d[v] = min{d[u] + ( 辺e=(u,v) の距離 )}」という更新式に従って更新します。

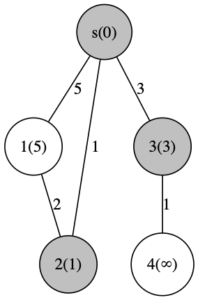
頂点1, 2, 3 の 3つを更新できました。そして（プログラム上では認知できませんが）2つの頂点の最短距離が求まっています。灰色の頂点は今後更新されることはありません。

もう一度、全ての辺を確認して最短距離を求めます。

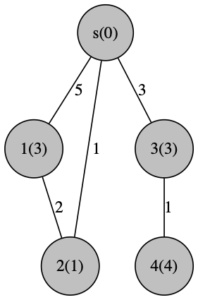
これで全ての頂点への最短距離が求まりました。実際に、|V-1| 回以内の更新で、全ての頂点への最短距離を求めることができています。

しかし、プログラムでは本当に全ての頂点の最短経路が求まったのかを、認知することはできてはいません。もう一度全ての辺を確認して、もう更新されることは無いのかを \(O(|E|)\) かけてチェックする必要があります。

以上の内容をまとめるとアルゴリズムは以下のようになります。

  1. 最短距離が更新されなくなるまで以下を繰り返す
    • 全ての辺に対して、「d[v] = min{d[u] + ( u から v への距離 )}」という更新式を利用して最短距離を更新する

仮に負の閉路が存在した場合は、|V-1| 回目の更新が終わった後でも最短距離が更新され続けてしまいます。よって、負の閉路の検出まで含めて考えると、|V| 回目の更新がされたら負の閉路が存在することになり、プログラムを終了させればよいです。

練習問題

※「距離を最大化したい」時は、グラフの辺に -1 をかければ 「最小化したい」に変わります。これはベルマンフォード法が負の辺が含まれていても利用できるために利用できる方法で、ダイクストラ法では使えません。

グラフグラフ,競プロ,重み付きグラフ,ベルマンフォード法,単一始点最短経路,最短経路,負の閉路,負の辺