ワーシャル・フロイド法での全点対最短経路を求めるアルゴリズム
任意の2頂点間の最短距離を求める問題を全点対最短経路問題といいます。
ワーシャル・フロイド法は、動的計画法を用いて全点対最短経路を求める有名なアルゴリズムです。
- 負の辺が含まれていても動作する
- 負の閉路がある場合は検出できる
という利点があります。
アルゴリズム
グラフ G = (V, E) に対するワーシャル・フロイド法は以下のようになります。
ワーシャル・フロイド法:(「dist[ i ][ j ] := 頂点 i から j への最短経路」を求める)
- dist[ i ][ j ] を以下のように初期化する
- 頂点 i から j へのコスト c(i, j) の辺がある時:dist[ i ][ j ] = c(i, j)
- i = j の時:dist[ i ][ i ] = 0
- 上記以外の時:dist[ i ][ j ] = INF
- dist を以下のように更新する
- 経由点 k = 0 から V-1 まで以下を行う
- 始点 i = 0 から V-1 まで以下を行う
- 終点 j = 0 から V-1 まで以下を行う
- i →* k →* j という経路(dist[ i ][ k ] + dist[ k ][ j ])が、dist[ i ][ j ] よりも小さければ更新
- 終点 j = 0 から V-1 まで以下を行う
- 始点 i = 0 から V-1 まで以下を行う
- 経由点 k = 0 から V-1 まで以下を行う
※ 以下のように頂点 k を経由した時の最短経路を考えます。
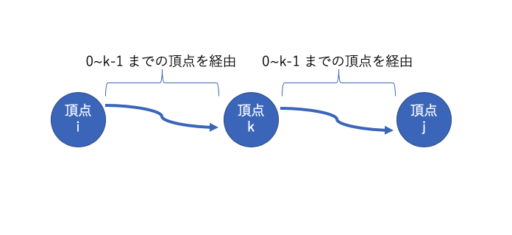
※ 具体例として、グラフとそれに対する dist の値の変化は以下のようになります。

初期化した時の dist:
0 5 -1 INF
INF 0 INF 3
INF INF 0 1
INF INF 4 0
最終的な dist:
0 5 -1 0
INF 0 7 3
INF INF 0 1
INF INF 4 0
※ dist の更新は 3重の for ループを利用して、以下のように簡単に書くことができます。
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
計算量
- \(O(|V|^3)\)
3重の for ループを使うので、計算量は \(O(|V|^3)\) になります。
実装例
先程の具体例であげたグラフの全点対最短経路を求めるプログラムです。
#include <bits/stdc++.h>
using namespace std;
const long long INF = 1e17;
/* warshall_floyd(dist)
入力:初期化した dist
計算量:O(|V|^3)
副作用:dis[i][j]にiからjへの最短路のコストを格納
*/
void warshall_floyd(vector<vector<long long>> &dist) {
int V = dist.size();
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}
}
}
}
vector<vector<long long>> dist = {{0, 5, -1, INF},
{INF, 0, INF, 3},
{INF, INF, 0, 1},
{INF, INF, 4, 0}};
int main() {
int V = (int)dist.size(); // 頂点数
warshall_floyd(dist); // 更新
// 出力
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][j] >= INF / 2) {
cout << "INF";
} else {
cout << dist[i][j];
}
if (j != V - 1) {
cout << " ";
}
}
cout << endl;
}
return 0;
}
ワーシャル・フロイドの応用
最短距離の経路復元
最短距離を求めるついでに、「1つ前にどの頂点を通ったか」を記録しておけば、終点から逆にたどっていくことで、最短距離の経路を復元することができます。
先程の関数を少し拡張すると以下のようになります。prev[ i ][ j ] という2次元の vector に i から j への最短路での j の1つ前の点を格納しています。
/* warshall_floyd(dist,prev)
入力:初期化した dist, prev
計算量:O(|V|^3)
副作用:dis[i][j]にiからjへの最短路のコストを格納、prev[i][j]にiからjへの最短路でのjの1つ前の点を格納
*/
void warshall_floyd(vector<vector<long long>> &dist, vector<vector<long long>> &prev) {
int V = dist.size();
for (int k = 0; k < V; k++) {
for (int i = 0; i < V; i++) {
for (int j = 0; j < V; j++) {
if (dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
prev[i][j] = prev[k][j];
}
}
}
}
}
/* get_path(prev, s, t)
入力:warshall_floyd で得た prev, スタート s, ゴール t
出力:s から t への最短路のパス
*/
vector<int> get_path(const vector<vector<long long>> &prev, int s, int t) {
vector<int> path;
for (int cur = t; cur != s; cur = prev[s][cur]) {
path.push_back(cur);
}
path.push_back(s);
reverse(path.begin(), path.end());
return path;
}
負の閉路の検出
グラフ G に負の閉路が含まれている場合は、「dist[ i ][ i ] の値が負になる」ような i が存在することになります。
例えば、 2→4→5→2 というような閉路があり、一辺のコストが -1 であれば 1周で -3 のコストになります。d[2][2], d[4][4], d[5][5] の値は最初0ですが、ワーシャル・フロイド法が終了すれば、全て -3 となってしまいます。
/* is_negative(dist)
入力:warshall_floyd で得た dist
出力:負の有向路を含むかどうか
*/
bool is_negative(const vector<vector<long long>> &dist) {
int V = dist.size();
for (int i = 0; i < V; i++) {
if (dist[i][i] < 0) {
return true;
}
}
return false;
}
ディスカッション
コメント一覧
まだ、コメントがありません