「写像12相」で典型的な数え上げ問題のパターン総整理

2020年10月23日数学二項係数,動的計画法,数え上げ,重複組合せ,写像12相,スターリング数,第2種スターリング数,ベル数

条件を満たすものが何通りあるか数える問題、すなわち数え上げ問題には様々なものがありますが、「$n$ 個の玉を $x$ 個の箱に分ける方法は何通りか」などといった、典型的なものはある程度パターン化して解くことができます。

この記事では、ある集合からある集合へのマッピングが何通り存在するのかを考えるときに便利な「写像12相（the twelvefold way）」について紹介し、これを通じて典型的な数え上げの方法を学ぶことを目的とします。

Contents

1. 写像12相とは
- 1.1. なぜ12通りなのか
2. 問題設定を一般化して写像として捉える
- 2.1. 写像の制限の仕方3通り
- 2.2. 集合の要素が区別できないとはどういうことか
3. [1] Nを区別する・Xを区別する・制限なし
4. [2] Nを区別する・Xを区別する・1個以内(単射)
5. [3] Nを区別する・Xを区別する・1個以上(全射)
6. [4] Nを区別しない・Xを区別する・制限なし
7. [5] Nを区別しない・Xを区別する・1個以内(単射)
8. [6] Nを区別しない・Xを区別する・1個以上(全射)
9. [7] Nを区別する・Xを区別しない・制限なし
10. [8] Nを区別する・Xを区別しない・1個以内(単射)
11. [9]Nを区別する・Xを区別しない・1個以上(全射)
12. [10] Nを区別しない・Xを区別しない・制限なし
13. [11] Nを区別しない・Xを区別しない・1個以内(単射)
14. [12]Nを区別しない・Xを区別しない・1個以上(全射)
15. 練習問題
16. おまけ：さらなる拡張…写像20相や写像30相へ
17. 参考

写像12相とは

まずは分かりやすく「$n$ 個の玉を $x$ 個の箱に分ける」状況を考え、詳しいことを後回しにして写像12相がどのようなものかを実際に見てみましょう。

「写像12相」は以下のように数え上げ問題の典型的な解き方をシステマチックに12通りに分類したものです。

玉($n$ 個)の区別	箱($x$ 個)の区別	制限なし	1個以内	1個以上
あり	あり	[1]. $x^n$	[2]. ${}_{x}{\mathrm P}_n$	[3]. $x!S(n,x)$ $=\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$
なし	あり	[4]. ${}_{x}{\mathrm H}_n={}_{n+x-1}{\mathrm C}_n$	[5]. ${}_{x}{\mathrm C}_n$	[6]. ${}_{x}{\mathrm H}_{n-x}$ $={}_{n-1}{\mathrm C}_{n-x}$ $={}_{n-1}{\mathrm C}_{x-1}$
あり	なし	[7]. $B(n,x):=\sum_{i=0}^{x}S(n,i)$	[8]. 1 ($n \leq x$ の時) 0 ($n > x$ の時)	[9]. $S(n,x)$
なし	なし	[10]. $p_{\leq x}(n):=\sum_{i=0}^{x}p_i(n)$	[11]. 1 ($n \leq x$ の時) 0 ($n > x$ の時)	[12]. $p_x(n)$ or $p_{\leq x}(n-x)$

写像12相（k 個のボールを n 個の箱に分ける方法）

※ 知らない記号もあるかと思います。簡単に説明すると

${}_{n}{\mathrm C}_k$ : 組み合わせ。二項係数。$n$ 個から順番を無視して $k$ 個選ぶ方法の数
${}_{n}{\mathrm H}_k$ : 重複組み合わせ。$n$ 種類から重複を無視して $k$ 個選ぶ方法の数
$S(n,k)$：第2種スターリング数。区別できる $n$ 個の要素を区別できない $k$ 個ちょうどのブロックに分割する方法の数
$B(n,k)$ : ベル数。区別できる $n$ 個の要素を区別できない $k$ 個以下のブロックに分割する方法の数
$p_k(n)$ : 自然数 $n$ を $k$ 個の 1 以上の整数に分割する方法の数。言い換えると、区別できない $n$ 個の要素を区別できない $k$ 個ちょうどのブロックに分割する方法の数
$p_{\leq k}(n)$ : よく $P(n,k)$ とも書く。自然数 $n$ を $k$ 個の 0以上の整数に分割する方法の数。言い換えると、区別できない $n$ 個の要素を区別できない高々 $k$ 個のブロックに分割する方法の数

詳しいことは後述しますが、このように問題設定で分類することで12種類の典型的な問題がシステマチックに解けるようになります。

なぜ12通りなのか

そもそもなぜ12通りなのか考えてみましょう。

玉を箱へ移す際にどのような制限を与えるか：3通り
- 制限がない
- 箱に入る数は1個以内
- 箱に入る数は1個以上
玉をそれぞれ区別するかどうか：2通り
箱をそれぞれ区別するかどうか：2通り

のそれぞれについて考えるので、全体で $3 \times 2 \times 2 = 12$ 通りになります。

問題設定を一般化して写像として捉える

※集合や写像に慣れていない方は難しく感じるかもしれません。その場合はここを飛ばして、先程の「n 個の玉を x 個の箱に分ける」モデルでの写像12相を使ってください。

先程までの写像12相は「$n$ 個の玉を $x$ 個の箱に分ける」というモデルで考えてみました。これを他の問題でも応用できるようにもう少し一般化してみましょう。

集合から集合へ移動させる方法を数えると考えると、「要素数が $n$ の集合 $N$ から要素数が $x$ の集合 $X$ への写像 $f: N \rightarrow X $ が何通り存在するか」と一般化できます。

先程の具体例と対応させると、

要素数が $n$ の集合 $N$：$n$ 個のボール
要素数が $x$ の集合 $X$：$x$ 個の箱
写像 $f: N \rightarrow X $：ボールを箱に分ける方法

というようになります。

※ それぞれの玉に対して箱は1つに定まるので、写像ではなく関数と言った方が良いかもしれません。

写像の制限の仕方3通り

「$n$ 個の玉を $x$ 個の箱に分ける」というモデルでは、玉を箱へ移す際にどのような制限を与えるかで以下のように3通り考えました。これを写像 $f: N \rightarrow X $ で考えると以下のようになります。

制限がない
$f$ は単射（箱に入る数は1個以内）
$f$ は全射（箱に入る数は1個以上）

このように考えると、写像の制限として性質が典型的なものを選んでいることがよく分かると思います。

集合の要素が区別できないとはどういうことか

「玉同士が区別できない」というような状況は、写像で一般化したときには一体どのような状況なのか考えてみましょう。

具体例で考える

まずは具体例で様子を見てみます。$N=\{1,2,3\}, X=\{a,b,c,d\}$ として以下のような写像 $f, g$ を考えてみましょう。

\begin{align}
&f(1)=f(2)=a, f(3)=b\\
&g(1)=g(3)=a, g(2)=b
\end{align}

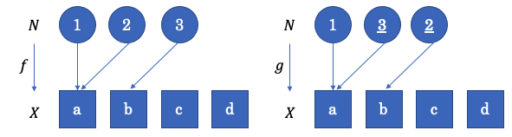
もし、$N$ が区別できないなら、これら2つの写像 $f, g$ は同じものとして扱うはずです。逆に$N$ が区別できるなら、これら2つの写像 $f, g$ は別のものとしてそれぞれ数える必要があります。

厳密な定義

具体例では、$f,g$ がどのような場合に同一視できるのかを見ました。この「写像の同値」を厳密に定義すると以下のようになります。

写像の同値の定義

集合 $N$ を区別しないとき、写像 $f, g: N \rightarrow X$ は以下の条件を満たせば同値であるという。
・全単射 $u: N \rightarrow N$ が存在して、任意の $i \in N$ について $f(u(i)) = g(i)$ を満たす。

基本的には、写像が同値であれば1つのものとして数え、同値でなければ別々のものとして数え上げることになります。

以上は $N$ が区別されるかどうかについて見ましたが、 $X$ が区別されるかどうかも同様に考えることができます。

一般化した形で写像12相を再掲します。

集合 $N$ の区別	集合$X$の区別	制限なし	単射	全射
あり	あり	[1]. $x^n$	[2]. ${}_{x}{\mathrm P}_n$	[3]. $x!S(n,x)$ $=\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$
なし	あり	[4]. ${}_{x}{\mathrm H}_n={}_{n+x-1}{\mathrm C}_n$	[5]. ${}_{x}{\mathrm C}_n$	[6]. ${}_{x}{\mathrm H}_{n-x}$ $={}_{n-1}{\mathrm C}_{n-x}$ $={}_{n-1}{\mathrm C}_{x-1}$
あり	なし	[7]. $B(n,x):=\sum_{i=0}^{x}S(n,i)$	[8]. 1 ($n \leq x$ の時) 0 ($n > x$ の時)	[9]. $S(n,x)$
なし	なし	[10]. $p_{\leq x}(n):=\sum_{i=0}^{x}p_i(n)$	[11]. 1 ($n \leq x$ の時) 0 ($n > x$ の時)	[12]. $p_x(n)$ or $p_{\leq x}(n-x)$

写像12相

それでは、この写像12相を1マスずつ確認していきましょう。分かりやすさのために基本的には「$n$ 個の玉を $x$ 個の箱に分ける」問題として考え、写像の話は補足的なものとします。

また、競技プログラミングの問題では答えが非常に大きくなってしまうので「素数で割ったあまり」を求めさせることが多いです。実装例やアルゴリズム解説では、基本的に「素数で割ったあまり」を求めることにします。

[1] Nを区別する・Xを区別する・制限なし

以下の場合を考えます。

$n$ 個の玉を区別する
$x$ 個の箱を区別する
玉の配り方にも制限を与えない

玉ごとに箱の選び方が $x$ 通り存在するため、全体としては $x^n$ 通りの分け方があります。

よって、基本的にはべき乗の計算ができれば良いです。多くのプログラミング言語では標準ライブラリとしてあります。しかし、素数で割ったあまりを求めることが多い競技プログラミングでは、自分で実装しなければならないことが多いです。

単純なアルゴリズムでは $O(n)$ の計算量がかかってしまいますが、繰り返し2乗法などを用いると $O(\log n)$ で計算ができます。

詳細は繰り返し二乗法によるべき乗(pow(x,n))の計算のアルゴリズムを確認して下さい。

[2] Nを区別する・Xを区別する・1個以内(単射)

以下の場合を考えます。

$n$ 個の玉を区別する
$x$ 個の箱を区別する
それぞれの箱には多くとも1個の玉しか入らない

1つ目の玉はどの箱にも入れられるので $x$ 通りの選択肢があり、2つ目の玉は残りの $x-1$ 通りの箱から選び… などと考えると、全体としては

$$ x(x-1)(x-2)…(x-n+1) = {}_{x}{\mathrm P}_n $$

通りになるので、順列の計算になります。

アルゴリズム

順列 ${}_{x}{\mathrm P}_n$ の計算は、単純に $x(x-1)(x-2)…(x-n+1)$ を計算してやるのが効果的でしょう。

順列 ${}_{x}{\mathrm P}_n$ のアルゴリズム：

$x$ から $(x-n+1)$ までの総乗を計算する(for 文などで順番に一つずつかければ良い)

計算量

$O(n)$

$x(x-1)(x-2)…(x-n+1)$ の計算に、$n$ 回の掛け算を行うので、計算量は $O(n)$ になります。

実装例

AOJ DPL_5_B Balls and Boxes 2 を解く実装例です。

#include <bits/stdc++.h>
using namespace std;
const int MOD = 1000000007;  // 素数

long long xPn(long long x, long long n) {
    long long ret = 1;
    for (long long i = 0; i < n; i++) {
        ret = ret * (x - i) % MOD;
    }
    return ret;
}

int main() {
    long long n, k;
    cin >> n >> k;
    cout << xPn(k, n) << endl;
    return 0;
}

[3] Nを区別する・Xを区別する・1個以上(全射)

以下の場合を考えます。

$n$ 個の玉を区別する
$x$ 個の箱を区別する
それぞれの箱には 1 個以上の玉が入るようにする

まず、$n$ 個の玉を $x$ 個のブロックに分けることを考えると、分け方は第2種スターリング数を用いて $S(n,x)$ と表すことが可能です。（これは第2種スターリング数の定義と考えても構いません。）

分けたブロックを並び替えて $x$ 個の箱に対応させることを考えると、これは $x!$ 通りとなります。

よって、全体では $x! S(n,x)$ を求めれば良いです。

ここで、第2種スターリング数の公式としてよく知られている

$$ S(n,x) = \frac{1}{x!}\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n $$

を用いると、

$$ x!S(n,x)=\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n $$

が成り立つことが分かります。

アルゴリズム

アルゴリズムの大まかな方針は、 [9] での第2種スターリング数 $S(n,x)$ を求める方法と同じです。詳しくは第2種スターリング数を求めるアルゴリズムを参考にしてください。念の為、今回の問題に合わせた方法を以下で解説します。

$x!S(n,x)$ を求める方法と、$\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$ を計算する方法の二種類があります。どちらも良いですが、後者に関しては二項係数は前計算を行うと $O(1)$ で求めることができるため、前者に比べて高速に計算ができます。

$x!S(n,x)$ を求めるアルゴリズム：

有名公式 $S(n,k) = k S(n-1,k) + S(n-1, k-1)$ を利用して、動的計画法により $S(n,x)$ を計算する。
$x!$ と 1. で求めた$S(n,x)$ をかけて $x!S(n,x)$ を求める

※慣例的に $S(0,0) = 1$ とします

$\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$ を求めるアルゴリズム：

$ (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$ を $i=0$ から $i=x$ まで全て足し合わせる

※ 二項係数は前計算を行っておくことで、素早く計算することができます。詳細は以下の記事を御覧下さい。
競プロでよく使う二項係数(nCk)を素数(p)で割った余りの計算と逆元のまとめ

計算量

$x!S(n,x)$ を求めるアルゴリズム： $O(xn)$
$\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$ を求めるアルゴリズム： $O(x \log n)$

$x!S(n,x)$ を求めるアルゴリズムでは、$S(n,x)$ を求めるための動的計画法により $n \times x$ のテーブルを更新することになります。1回あたりの更新は定数時間なので、$O(xn)$ だけかかってしまいます。

$\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$ を求めるアルゴリズムでは、二項係数については前計算を行うことで $O(1)$ 程度で計算できますが、$i^n$ を求めるのに $O(\log n)$ だけかかるので、$x$ 回分計算すると全体では $O(x \log n)$ になります。

実装例($x!S(n,x)$)

AOJ DPL_5_C Balls and Boxes 3 を解く実装例です。動的計画法によって第2種スターリング数を求めます。

#include <bits/stdc++.h>
using namespace std;
const int MOD = 1000000007;  // 素数

int main() {
    long long N, K;
    cin >> N >> K;

    vector<vector<long long>> S(N + 1, vector<long long>(K + 1, 0));
    S[0][0] = 1;

    for (long long n = 1; n < N + 1; n++) {
        for (long long k = 1; k < K + 1; k++) {
            S[n][k] = (k * S[n - 1][k] + S[n - 1][k - 1]) % MOD;
        }
    }

    long long ans = S[N][K];
    for (int k = 1; k <= K; k++) {
        ans = ans * k % MOD;
    }

    cout << ans << endl;

    return 0;
}

実装例($\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$)

AOJ DPL_5_C Balls and Boxes 3 を解く実装例です。二項係数によって求めます。

二項係数の計算方法がよくわからない場合は、競プロでよく使う二項係数(nCk)を素数(p)で割った余りの計算と逆元のまとめをご確認ください。

この実装例では、一旦 $S(n,x) = \frac{1}{x!}\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n$ を求めてから、$x!$ を掛けています。

#include <bits/stdc++.h>
using namespace std;
const int MOD = 1000000007;  // 素数
vector<long long> fact, fact_inv, inv;

/*  init_nCk :二項係数のための前処理
    計算量:O(n)
*/
void init_nCk(int SIZE) {
    fact.resize(SIZE + 5);
    fact_inv.resize(SIZE + 5);
    inv.resize(SIZE + 5);
    fact[0] = fact[1] = 1;
    fact_inv[0] = fact_inv[1] = 1;
    inv[1] = 1;
    for (int i = 2; i < SIZE + 5; i++) {
        fact[i] = fact[i - 1] * i % MOD;
        inv[i] = MOD - inv[MOD % i] * (MOD / i) % MOD;
        fact_inv[i] = fact_inv[i - 1] * inv[i] % MOD;
    }
}

/*  nCk :MODでの二項係数を求める(前処理 int_nCk が必要)
    計算量:O(1)
*/
long long nCk(int n, int k) {
    assert(!(n < k));
    assert(!(n < 0 || k < 0));
    return fact[n] * (fact_inv[k] * fact_inv[n - k] % MOD) % MOD;
}

// べき乗
long long pow(long long x, long long n) {
    long long ret = 1;
    while (n > 0) {
        if (n & 1) ret = ret * x % MOD;
        x = x * x % MOD;
        n >>= 1;
    }
    return ret;
}

// 第2種スターリング数
long long S(long long n, long long k) {
    long long ret = 0;
    for (long long i = 0; i <= k; i++) {
        if ((k - i) % 2 == 0) {
            ret = ret + nCk(k, i) * pow(i, n) % MOD;
            ret %= MOD;
        } else {
            ret = ret + (MOD - nCk(k, i) * pow(i, n) % MOD);
            ret %= MOD;
        }
    }
    ret = ret * fact_inv[k] % MOD;
    return ret;
}

int main() {
    init_nCk(10000000);
    long long N, K;
    cin >> N >> K;

    cout << (fact[K] * S(N, K)) % MOD << endl;

    return 0;
}

[4] Nを区別しない・Xを区別する・制限なし

以下の場合を考えます。

$n$ 個の玉を区別しない
$x$ 個の箱を区別する
玉の配り方にも制限を与えない

$x$ 個の箱それぞれに対して、何個の玉が入るかを考えることになります。つまり、$x$ 種類の箱について重複を許して $n$ 回玉を入れるものを選ぶことになります。

これは以下の重複組み合わせであり、重複組合せは二項係数を用いて計算できることが知られています。

$${}_{x}{\mathrm H}_n={}_{n+x-1}{\mathrm C}_n$$

二項係数の計算方法は競プロでよく使う二項係数(nCk)を素数(p)で割った余りの計算と逆元のまとめをご確認ください。

[5] Nを区別しない・Xを区別する・1個以内(単射)

以下の場合を考えます。

$n$ 個の玉を区別しない
$x$ 個の箱を区別する
それぞれの箱には多くとも1個の玉しか入らない

[4] の場合と似ていますが、今回は重複して選ぶことを許していません。つまり、各箱に入る玉は高々1つになります。

$x$ 個の箱から、玉を入れることになる $n$ 個の箱を選ぶことになるので、${}_{x}{\mathrm C}_n$ になります。

二項係数の計算方法は競プロでよく使う二項係数(nCk)を素数(p)で割った余りの計算と逆元のまとめをご確認ください。

[6] Nを区別しない・Xを区別する・1個以上(全射)

以下の場合を考えます。

$n$ 個の玉を区別しない
$x$ 個の箱を区別する
それぞれの箱には 1 個以上の玉が入るようにする

「全ての箱に1個以上の玉が入る」という制約があるので、あらかじめ玉を $x$ 使って箱に入れておくことを考えましょう。

すると、問題は [4] の状況設定とほぼ同じになります。異なるのは玉の数が $n-x$ 個になっていることだけです。これは以下のように重複組み合わせを用いて計算することができます。

$${}_{x}{\mathrm H}_{n-x}={}_{n-1}{\mathrm C}_{n-x}={}_{n-1}{\mathrm C}_{x-1}$$

二項係数の計算方法は競プロでよく使う二項係数(nCk)を素数(p)で割った余りの計算と逆元のまとめをご確認ください。

[7] Nを区別する・Xを区別しない・制限なし

以下の場合を考えます。

$n$ 個の玉を区別する
$x$ 個の箱を区別しない
玉の配り方にも制限を与えない

これは区別できる $n$ 個の要素を区別できない高々 $k$ 個のブロックに分割する方法の数と考えることができます。

よって、分割するブロックの数について固定して、 0 から $k$ まですべて足し合わせることを考えると、答えは $\sum_{i=0}^{x}S(n,i)$ になります。

この数をベル数と言い、以下のように表します。

$$B(n,x):=\sum_{i=0}^{x}S(n,i)$$

単純にスターリング数を求めてから和を計算しても良いのですが、別の方法で求めることもできます。

詳細はベル数を求めるアルゴリズム：第2種スターリング数の和を効率的に計算するを確認して下さい。

[8] Nを区別する・Xを区別しない・1個以内(単射)

以下の場合を考えます。

$n$ 個の玉を区別する
$x$ 個の箱を区別しない
それぞれの箱には多くとも1個の玉しか入らない

それぞれの箱には 1 個までしか玉が入らないので、どのような入れ方であっても $n$ 個の箱に 1 つずつ玉が入ることになります。玉は区別しますが、箱は区別しないので、玉を入れ終わった時の状態はたった一つだけです。

よって、$n \leq x$ の時は玉を全て箱に入れることができるので 1 通り、$n > x$ の時は玉を箱に全て入れることができないので 0 通りになります。

これは if 文などを用いることで用意に実装ができます。

[9]Nを区別する・Xを区別しない・1個以上(全射)

以下の場合を考えます。

$n$ 個の玉を区別する
$x$ 個の箱を区別しない
それぞれの箱には 1 個以上の玉が入るようにする

これは、第2種スターリング数の性質であり、定義ということもできます。第2種スターリング数とは、区別できる $n$ 個の要素を区別できない $k$ 個のブロックに分割する方法の総数でした。

求め方については第2種スターリング数を求めるアルゴリズムを参考にしてください。

[10] Nを区別しない・Xを区別しない・制限なし

以下の場合を考えます。

$n$ 個の玉を区別しない
$x$ 個の箱を区別しない
玉の配り方にも制限を与えない

これは、「区別しない $n$ 要素を、区別しない高々 $x$ 個のブロックに分ける方法」とも言えます。

よって $p_{\leq x}(n)$ を計算すれば良いです。

※ $p_{\leq k}(n)$ : よく $P(n,k)$ とも書く。自然数 $n$ を $k$ 個の 0以上の整数に分割する方法の数。言い換えると、区別できない $n$ 個の要素を区別できない高々 $k$ 個のブロックに分割する方法の数

詳しい計算方法は自然数nをk個の0以上の整数に分割する方法の総数を求めるアルゴリズムを確認して下さい。

[11] Nを区別しない・Xを区別しない・1個以内(単射)

以下の場合を考えます。

$n$ 個の玉を区別しない
$x$ 個の箱を区別しない
それぞれの箱には多くとも1個の玉しか入らない

これはほぼ [8] の状況と同じです。

それぞれの箱には 1 個までしか玉が入らないので、どのような入れ方であっても $n$ 個の箱に 1 つずつ玉が入ることになります。箱は区別しないので、玉を入れ終わった時の状態はたった一つだけです。

よって、$n \leq x$ の時は玉を全て箱に入れることができるので 1 通り、$n > x$ の時は玉を箱に全て入れることができないので 0 通りになります。

これは if 文などを用いることで用意に実装ができます。

[12]Nを区別しない・Xを区別しない・1個以上(全射)

以下の場合を考えます。

$n$ 個の玉を区別しない
$x$ 個の箱を区別しない
それぞれの箱には 1 個以上の玉が入るようにする

これは $p_x(n)$ の定義とも言えるので、$p_x(n)$ を計算すれば良いです。

※ $p_k(n)$ : 自然数 $n$ を $k$ 個の 1 以上の整数に分割する方法の数。言い換えると、区別できない $n$ 個の要素を区別できない $k$ 個ちょうどのブロックに分割する方法の数

もしくは、「それぞれの箱には 1 個以上の玉が入るようにする」という制限があるので、先に $x$ 個の玉を 1 つずつそれぞれの箱に入れることを考えてみましょう。すると状況はほぼ [10] と同じになり、玉の個数は $n-x$ になっているので、$p_{\leq x}(n-x)$ を計算すれば良いことになります。

$p_x(n)$ は自然数nをk個の1以上の整数に分割する方法の総数を求めるアルゴリズムを参考にして求めて下さい。

$p_{\leq x}(n-x)$ は自然数nをk個の0以上の整数に分割する方法の総数を求めるアルゴリズムを参考にして求めて下さい。

練習問題

AOJで写像12相の全ての問題をチェックできます。

おまけ：さらなる拡張…写像20相や写像30相へ

写像12相の分類をさらに拡張して、写像20相や写像30相に一般化することなどが提案されています。

例えば、Kenneth P. Bogart, 2002, “Combinatorics Through Guided Discovery" では写像の制限として「$f$ が全単射であること」を加え、$X$ の要素の順番を考慮するなどして、全部で20通りの分類を行っています。

また、Proctor, R. A., 2006, Let’s Expand Rota’s Twelvefold Way For Counting Partitions! では、写像30相に拡張し、さらなる分類の提案も行っているようです。

参考

「写像12相」を総整理！〜数え上げ問題の学びの宝庫〜 – Qiita：写像12相という単語をはじめて聞く方はこちらを読んでみると分かりやすいかもしれません
Richard P. Stanley, 2011, “Enumerative Combinatorics"：数え上げの教科書です。写像12相について載っています。
Kenneth P. Bogart, 2002, “Combinatorics Through Guided Discovery"：写像20相に拡張しています
Proctor, R. A., 2006, Let’s Expand Rota’s Twelvefold Way For Counting Partitions!：写像30相に拡張した論文です

2020年10月23日数学二項係数,動的計画法,数え上げ,重複組合せ,写像12相,スターリング数,第2種スターリング数,ベル数

ディスカッション

コメント一覧

まだ、コメントがありません

玉(\(n\) 個)の区別	箱(\(x\) 個)の区別	制限なし	1個以内	1個以上
あり	あり	[1]. \(x^n\)	[2]. \({}_{x}{\mathrm P}_n\)	[3]. \(x!S(n,x)\) \(=\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n\)
なし	あり	[4]. \({}_{x}{\mathrm H}_n={}_{n+x-1}{\mathrm C}_n\)	[5]. \({}_{x}{\mathrm C}_n\)	[6]. \({}_{x}{\mathrm H}_{n-x}\) \(={}_{n-1}{\mathrm C}_{n-x}\) \(={}_{n-1}{\mathrm C}_{x-1}\)
あり	なし	[7]. \(B(n,x):=\sum_{i=0}^{x}S(n,i)\)	[8]. 1 (\(n \leq x\) の時) 0 (\(n > x\) の時)	[9]. \(S(n,x)\)
なし	なし	[10]. \(p_{\leq x}(n):=\sum_{i=0}^{x}p_i(n)\)	[11]. 1 (\(n \leq x\) の時) 0 (\(n > x\) の時)	[12]. \(p_x(n)\) or \(p_{\leq x}(n-x)\)

集合 \(N\) の区別	集合\(X\)の区別	制限なし	単射	全射
あり	あり	[1]. \(x^n\)	[2]. \({}_{x}{\mathrm P}_n\)	[3]. \(x!S(n,x)\) \(=\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n\)
なし	あり	[4]. \({}_{x}{\mathrm H}_n={}_{n+x-1}{\mathrm C}_n\)	[5]. \({}_{x}{\mathrm C}_n\)	[6]. \({}_{x}{\mathrm H}_{n-x}\) \(={}_{n-1}{\mathrm C}_{n-x}\) \(={}_{n-1}{\mathrm C}_{x-1}\)
あり	なし	[7]. \(B(n,x):=\sum_{i=0}^{x}S(n,i)\)	[8]. 1 (\(n \leq x\) の時) 0 (\(n > x\) の時)	[9]. \(S(n,x)\)
なし	なし	[10]. \(p_{\leq x}(n):=\sum_{i=0}^{x}p_i(n)\)	[11]. 1 (\(n \leq x\) の時) 0 (\(n > x\) の時)	[12]. \(p_x(n)\) or \(p_{\leq x}(n-x)\)

「写像12相」で典型的な数え上げ問題のパターン総整理

写像12相とは

なぜ12通りなのか

問題設定を一般化して写像として捉える

写像の制限の仕方3通り

集合の要素が区別できないとはどういうことか

具体例で考える

厳密な定義

[1] Nを区別する・Xを区別する・制限なし

[2] Nを区別する・Xを区別する・1個以内(単射)

アルゴリズム

計算量

実装例

[3] Nを区別する・Xを区別する・1個以上(全射)

アルゴリズム

計算量

実装例(\(x!S(n,x)\))

実装例(\(\sum_{i=0}^{x} (-1)^{x-i} {}_{x}{\mathrm C}_i i^n\))

[4] Nを区別しない・Xを区別する・制限なし

[5] Nを区別しない・Xを区別する・1個以内(単射)

[6] Nを区別しない・Xを区別する・1個以上(全射)

[7] Nを区別する・Xを区別しない・制限なし

[8] Nを区別する・Xを区別しない・1個以内(単射)

[9]Nを区別する・Xを区別しない・1個以上(全射)

[10] Nを区別しない・Xを区別しない・制限なし

[11] Nを区別しない・Xを区別しない・1個以内(単射)

[12]Nを区別しない・Xを区別しない・1個以上(全射)

練習問題

おまけ：さらなる拡張…写像20相や写像30相へ

参考