組み合わせゲーム理論の基礎とGrundy数での勝敗判定アルゴリズム
競技プログラミングなどで頻出のテーマである組み合わせゲームやGrundy数についてまとめました。
前半は全ての方に向けての内容で、プログラム例や競技プログラミング特有の話題については後半にあります。
組み合わせゲームとは
組み合わせゲーム(Combinatorial games)とは以下のような特徴を持った二人で行うゲームのことを言います。
- 確定:ランダム性がない
- 完全情報:全ての情報が全てのプレイヤーに公開されている
組み合わせゲームの例
以下のような多くのゲームが組み合わせゲームに分類されます。
- オセロ
- 将棋
- チェス
- 囲碁
- Nim
- …
これらのどれもが、二人で行うゲームで、確定であり完全情報でもあります。
特殊な組み合わせゲーム
組み合わせゲームの中でも特殊な性質を持つものは名前がついており、解析がしやすいものがいくつかあります。
二人零和有限確定完全情報ゲーム
組み合わせゲームに以下の性質がついたものを、二人零和有限確定完全情報ゲームと言います。
- 零和:一方のプレイヤーが利益を得ると、もう一方のプレーヤーに同等の不利益がある
- 有限:ゲームが有限の手順で終了する
オセロなどは二人零和有限確定完全情報ゲームの一種です。
不偏ゲーム(公平ゲーム)
「二人零和有限確定完全情報ゲーム」のうち、どの場面において・どちらの手番であっても、打てる手の候補が変わらないものを言います。
つまり、組み合わせゲームに以下の性質がついたものです。
- 零和:一方のプレイヤーが利益を得ると、もう一方のプレーヤーに同等の不利益がある
- 有限:ゲームが有限の手順で終了する
- 場面が同じなら、プレイヤーが違うことで操作の候補が変わることがない
チェスやオセロなどはプレイヤーによって打てる手が変化してしまうので、不偏ゲームではありません。後述する Nim などのゲームが不偏ゲームに分類されます。
代表的な不偏ゲーム Nim
不偏ゲームの代表例である Nim を見ていきましょう。
Nim のルール
先手と後手は、複数用意したコインの山から以下のルールで交互にコインを取り合い、コインを取れなくなったほうが負けとなる。
- コインの山を一つ選んで、その山から一枚以上のコインを好きなだけ取る

Nim は不偏ゲーム
Nim は以下の特徴を満たしているので不偏ゲームと言えます。
- 二人で交互にプレイする
- 確定:ランダム性がない
- 完全情報:全ての情報(山の状態)が全てのプレイヤーに公開されている
- 零和:一方のプレイヤーが利益を得ると、もう一方のプレーヤーに同等の不利益がある
- 有限:コインは毎回1つ以上減るので、いつか終了する
- 場面(山の状態)が同じなら、取れる手の候補は変わらない
Nim には必勝法が存在する
不偏ゲームである Nim は、はじめにコインの山の状態が分かれば、先手と後手が最適な手を取る場合、どちらが勝つかが分かってしまいます。
特に山の数が少ない場合についていくつか確認してみましょう。
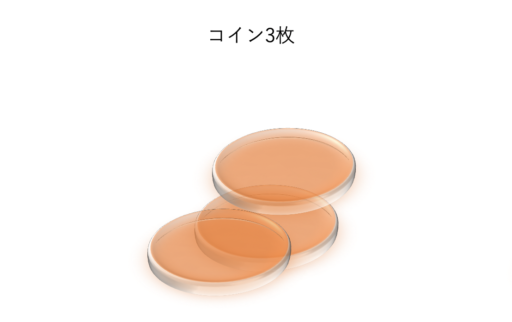
山が1つの時(先手必勝)
コインの山が一つの時を考えます。
その山に何枚のコインがあったとしても、先手が全てのコインを取ってしまうのが最適です。
次に後手は取れるコインが無くなってしまうので、先手必勝と言えます。
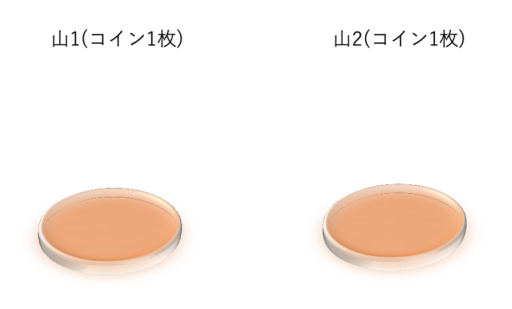
山が2つでコインの数が1枚ずつの時(後手必勝)
山が2つあって、そのコインの数が一枚ずつの時を考えます。
先手は必ず一枚コインを取る必要があるので、後手は最後の1枚のコインを取ることができます。よって後手必勝です。
これは、先手がコインを取ると、「手番を入れ替えて “山が一つの時" の状態からスタートする」とも考えることができます。不偏ゲームの特徴です。
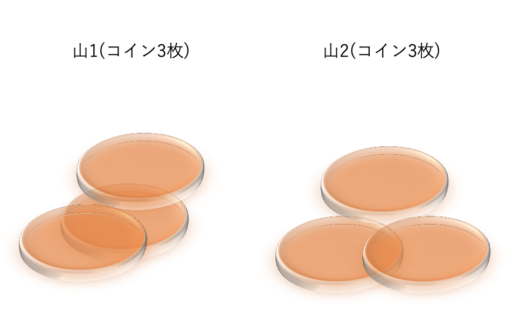
山が2つでコインの数が同じ時(後手必勝)
コインの山が2つで、そのコインの数が等しい場合を考えます(1枚ずつでなくても良い)。
先手が1つの山から全てのコインを取ってしまうと、「手番を入れ替えて “山が一つの時" の状態からスタートする」ことになるので先手の負けです。
先手が山にあるコインを残すように取っても、後手がもう一方の山から同じ数を取れば、同様に “山が2つでコインの数が同じ時" に戻ってしまいます。最終的に、"山が2つでコインの数が1枚ずつの時" になってしまうので、やはり先手の負けです。
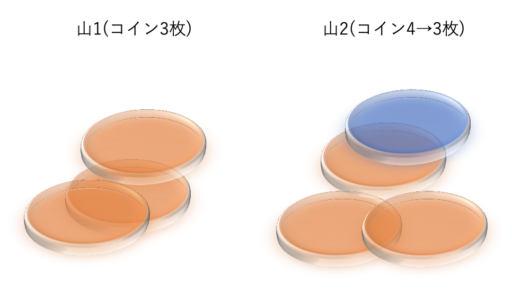
山が2つでコインの数が違う時(先手必勝)
コインの山が2つあるが、コインの数が違う時を考えます。
先手は、コインの数が多い方からコインを取って、2つの山のコインの数が等しくなるようにすれば良いです。
すると、「手番を入れ替えて “山が2つでコインの数が同じ時" の状態からスタートする」ことになるので、もともと先手だったほうが必ず勝つことができます。
先手必勝か後手必勝かを判定する方法
まずは結論から述べます。
各山にあるコインの枚数を、\(\{a_1, a_2, a_3, …, a_N\}\) とした時に、全ての数を XOR(繰り上がりの無い足し算) で計算した時の値、
- XOR sum : \(a_1 \oplus a_2 \oplus a_3 \oplus … \oplus a_N\)
を計算すると、
- XOR sum が 0 でない:先手の勝ち
- XOR sum が 0 である:後手の勝ち
となります。
なぜ XOR sum で判定できるのか?
XOR sum の値に注目してみると実は以下が成り立ちます。
- XOR sum が 0 でない時(勝ち):うまくコインを取れば、XOR sum を0 にすることができる
- XOR sum が 0 の時(負け):どの山からどのようにコインを取っても、XOR sum を 0 にすることができない。
- 負けるのは、全てのコインが無くなった時で、その時のXOR sum の値は 0
これらを踏まえて、始め XOR sum が 0 でない時を例に考えてみると、以下のようにゲームが進行します。
- 始めの XOR sum が non-zero(0でない)時、以下が繰り返される
- 先手(non-zero):上手くコインを取って、XOR sumを 0 に
- 後手(0):どう取っても XOR sum は non-zero に
- 最終的に全てのコインがなくなり、その時 XOR sum の値は 0 なので後手の負け
よって、先手が最善な手を打ち続ければ、自身の手番での XOR sum を non-zero に・相手の手番では 0 に毎回できるので、必ず勝つことができます。
はじめの XOR sum が 0 であれば、逆に後手必勝となります。
XOR sum を non-zero から 0 にする方法
以下のように上手く石を取ると、XOR sum を non-zero から 0 にすることができます。
- 2進数で見た時に、XOR sum の一番上の 1 のビットが立っている桁を見て、それと同じ桁に 1 のビットがある山を選ぶ
- その山から、XOR sum の 1 のビットだけが全て反転するようにコインを取る
具体例
具体的に見てみましょう。山にあるコインが、\(3(011_2), 4(100_2), 6(110_2)\) である時を考えてみます。
- XOR sum の値:\(3(011_2) \oplus 4(100_2)\oplus 6(110_2) = 1(001_2)\)
となるので、今回は先手必勝です。先手は、この中から上手くコインを取って、XOR sum を 0 にする必要があります。
先ほど説明した方法に則って考えると、
- XOR sum \(= 1(001_2)\) では、一番上の 1 のビットは 0 桁目。0桁目が 1 になっているのは、\(3(011_2)\) の山のみ
- \(3(011_2)\) の山から、XOR sum の 1 のビットだけが全て反転するようにコインを取るには、1 つのコインを取り除けば良い。
となります。よって後手の手番では
- XOR sum の値:\(2(010_2) \oplus 4(100_2)\oplus 6(110_2) = 0(000_2)\)
XOR sum の値は 0 となってしまいます。後手はどのようなコインのとり方をしても、XOR sum を 0 にすることができません。
以下同様にゲームを進めていきますが、先手が最善手を取り続ければ必ず勝つことができます。
不偏ゲームに対するGrundy数の概念
Grundy数(Nim数/Nimber) はどんな不偏ゲームに対しても定義することができる、ゲームの状態を表す数の1種です。
Nim における 「1つの山にあるコイン数」や「XOR sumの値」を抽象化したもので、これを理解すると不偏ゲームを簡単に解析することができるようになります。
定義を説明するには色々と準備が必要なので、まずは目的から説明します。
Grundy数の目的
Grundy数の計算方法はあとで詳しく述べるとして、気持ちをざっくり説明すると
- Grundy数が0なら負け
- Grundy数が0でないなら勝ち
というものを表します。不偏ゲームに対して、このGrundy数をうまく計算することができれば、どちらが必勝なのかを解析することができます。
これはちょうど、先程までに説明した Nim における XOR sum の値に対応します。こちらも 0 なら負け、 non-zero なら勝ちを表していました。
準備:Mex とは
Grundy数の前に、Mex: 最小除外数(Minimum excludant) についての説明をします。
mex関数は、集合を受け取って、集合に含まれない最も小さい非負整数を返す関数のことです。Grundy数の定義にこれを利用します。
mex関数の例
- mex({0}) = 1
- mex({0, 1}) = 2
- mex({0, 1, 2}) = 3
- mex({0, 2, 3}) = 1
- mex({2}) = 0
- mex({}) = 0
改めて:Grundy数の定義
Grundy数は、以下のように再帰的に定めることができます。プレイヤーの手番が変わる度に、ゲームの状態が変化すると考え、ゲームの状態ごとにGrundy数を計算することができます。
終了状態 P での Grundy 数 = 0
ある状態 P での Grundy数 = mex(「Pから到達可能な状態 P’ のGrundy数」の集合 )
気持ちとしては、以下を満たすように定義をしています。
- 始めた瞬間に先手が負けるような時(終了状態)のGrundy数は 0 にする
- どのように手を打っても「次の状態でのGrundy数が0にならない」場合は、Grundy数を 0 にする
このような定め方をすることで、
- Grundy数が正(non-zero):上手く手を選ぶと次の状態での Grundy数を 0 にできる →先手必勝
- Grundy数が0:どのように手を選んでも、次の Grundy数は non-zero →後手必勝
というようになります。Nim の XOR sum でも同様の状況になっていました。
Grundy数の具体例
不偏ゲーム全てに対して Grundy 数を定めることができるので、さきほどのNimについても同様に定めることができます。
Nimで山が一つだけの時
簡単のために、まずは山が一つしか無い時を考えてみましょう。コインの枚数とGrundy数の対応は以下のようになります。
| コインの枚数 n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| Grundy数 g(n) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
コインの枚数とGrundy数がちょうど対応しています。一枚以上残っていれば全てのコインを取ることができるので先手必勝です。0枚しかなければ開始時点で先手が負けてしまうので、後手必勝となります。
Nimで山2つでコインが(3, 1) のとき
左から順番に Grundy数を求めていくと以下のようになります。
| コインの枚数 (n,n) | (0,0) | (1,0) | (2,0) | (3,0) | (0,1) | (1,1) | (2,1) | (3,1) |
| Grundy数 g((n,n)) | 0 | 1 | 2 | 3 | 1 | 0 | 3 | 2 |
詳しくは以下のように計算することができます。
- g((0,0)) : 終了状態なので 0
- g((1,0)) = mex( {g(0,0)} ) = mex( {0} ) = 1
- g((2,0)) = mex( {g(0,0),g(1,0)} ) = mex( {0,1} ) = 2
- g((3,0)) = mex( {g(0,0),g(1,0),g(2,0)} ) = mex( {0,1,2} ) = 3
- g((0,1)) = mex( {g(0,0)} ) = mex( {0} ) = 1
- g((1,1)) = mex( {g(0,1), g(1,0)} ) = mex( {1} ) = 0
- g((2,1)) = mex( {g(0,1), g(1,1), g(2,0)} ) = mex( {1,0,2} ) = 3
- g((3,1)) = mex( {g(0,1), g(1,1), g(2,1), g(3,0)} ) = mex( {1,0,3} ) = 2
不偏ゲームを分割してXORで勝敗を判定する
スプレイグ・グランディの定理(Sprague Grundy Theorem) と呼ばれるものを利用すると、全ての不偏ゲームを Nim と同様に XOR を用いて勝ち負けを判定することができます。
N 個の部分不偏ゲームを並行して行うような不偏ゲームについて以下が成立する。
先手と後手が最適に行動すれば、N個の部分不偏ゲームに対する全てのGrundy数に対して取った XOR の値が non-zero のとき先手必勝となり、0のとき後手必勝となる。
これだけでは分かりにくいので具体例をみてみましょう。
具体例: Nim への適用
スプレイグ・グランディの定理は以下のように Nim 自体に適用することができます。
- Nim は N個の山がある時、「1個の山についてのNim」を部分的な不偏ゲームとして N 個並行して行う不偏ゲームと見ることができる
- 「1個の山についてのNim」についてGrundy数を考えると、「Grundy数=コインの枚数」になる
- N個の部分不偏ゲームのGrundy数についての XOR sum の値が、non-zero のとき先手必勝となり、0のとき後手必勝となる
Nim を 「1つの山についてのNim」を組み合わせてできたゲームだと捉えることで、このように定理の適用ができます。これは実際の Nim の必勝判定方法と一致しています。
一般の不偏ゲームへの適用手順
以下の手順で、任意の不偏ゲームに対してスプレイグ・グランディの定理を利用することができます。
- 不偏ゲームを部分ゲームに分割する
- それぞれの部分ゲームに対して、その状況での Grundy数を計算する
- 計算したGrundy数全てに対しての XOR を取る
- XOR sum の値が、non-zero のとき先手必勝となり、0のとき後手必勝となる
それでは、通常の Nim 以外の不偏ゲームについての問題例を見ながら理解を深めていきましょう。
問題例:yukicoder No.2 素因数ゲーム
自然数 N が与えられる。先手と後手は以下の操作を繰り返し、先に操作できなくなった方が負けになる。二人が最善を尽くすとどちらが勝つか?
- 「Nの素因数」で、今ある数を一回以上割る。割り切れるなら好きな回数割って良い。
制約
- \(2 \leq N \leq 100,000,000\)
考え方
まずこのゲームですが、以下の特徴を捉えると不偏ゲームであると言えます。
- 二人で交互にプレイする
- 確定:ランダム性がない
- 完全情報:全ての情報(残った数)が全てのプレイヤーに公開されている
- 零和:一方のプレイヤーが利益を得ると、もう一方のプレーヤーに同等の不利益がある
- 有限:割る度に数は減るので、最終的に操作が行えなくなる(1となって割ることができない)
- 場面(残った数)が同じなら、先手と後手が入れ替わっても取れる手の候補は変わらない
素因数で割るので、とりあえず素因数分解をしてみると形が見えてきます。
具体的に N=24 で考えてみると
- \(24 = 2^3 × 3^1\)
となります。この状態で、例えば 2 で 2 回割ることにすると、
- \(2^1 × 3^1\)
などと変化します。
以上を良く見ると、操作は「素数を選んで、その肩に乗っている数字を1以上減らす」と言い換えることができ、実は肩の数字を「山にあるコインの枚数」と捉えると Nim とほぼ同じゲームであると分かりました。
解法
Nim と同じように XOR sum の値を使いましょう。
- N \(= p_1^{a_1} × p_2^{a_2} × \cdots × p_n^{a_n}\) などと素因数分解する
- (\(a_1, a_2, \cdots, a_n\) を 「n個の山にあるコインの枚数」と捉えて Nim と同一視する)
- \(a_1 \oplus a_2 \oplus a_3 \oplus … \oplus a_n\) が non-zero なら先手の必勝、0なら後手の必勝となる
C++ での実装例
xor 演算子は、C++において、^ で表されます。
素因数分解についてはこちらを参考にしてください。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
/* prime_factor(n)
入力:整数 n
出力:nの素因数分解
計算量:O(√n)前後
*/
template <typename T>
map<T, T> prime_factor(T n) {
map<T, T> ret;
for (T i = 2; i * i <= n; i++) {
T tmp = 0;
while (n % i == 0) {
tmp++;
n /= i;
}
ret[i] = tmp;
}
if (n != 1) ret[n] = 1;
return ret;
}
ll N;
int main() {
cin >> N;
map<ll, ll> p_fac = prime_factor(N); // first:素数p second: pで何回割り切れるか
// 肩の数を格納して Nim とみなす
vector<int> nim;
for (auto p : p_fac) {
int num = p.second;
nim.push_back(num);
}
// XOR sum の計算
int xor_sum = 0;
for (auto t : nim) {
xor_sum ^= t;
}
if (xor_sum == 0) { // 後手必勝
cout << "Bob" << endl;
} else { // 先手必勝
cout << "Alice" << endl;
}
return 0;
}
問題例:yukicoder No.103 素因数ゲーム リターンズ
N 個の整数 \(M_1, M_2, M_3, \cdots, M_N\) が与えられる。先手と後手は以下の操作を繰り返し、先に操作できなくなった方が負けになる。二人が最善を尽くすとどちらが勝つか?
- \(i\) を一つ選び「\(M_i\) の素因数」で、\(M_i\) を1 or 2回割る。割り切れなければ割ってはいけない。
制約
- \(1 \leq N \leq 100\)
- \(2 \leq M_i \leq 10^4\)
考え方
これも不偏ゲームの一つです。特徴を満たしているか確かめてみてください。
1回の操作では、N 個の整数の中から 1つしか操作することができません。この条件から「1 個の整数しか与えられなかった時のゲーム」を並行して N個進めていると考えることができます。
よって、スプレイグ・グランディの定理を以下のように適用することができます。
- 不偏ゲームを部分ゲーム(「1 個の整数しか与えられなかった時のゲーム」)N個に分割する
- それぞれの部分ゲームに対して、その状況での Grundy数を計算する
- 計算したGrundy数全てに対しての XOR を取る
- XOR sum の値が、non-zero のとき先手必勝となり、0のとき後手必勝となる
「1 個の整数 M しか与えられなかった時のゲーム」のGrundy数
部分ゲームを見ていきましょう。全体に比べて単純化されているので考えやすくなることが多いです。
割ることができる回数は、1回 or 2回という制限がついているので、前問とは少し状況が異なります。
具体的に M = 24 について見てみましょう。
- \(24 = 2^3 × 3^1\)
となります。この状態で、例えば 2 で 2 回割ることにすると、
- \(2^1 × 3^1\)
などと変化します。
この部分ゲームと前問のゲームとの違いは、個数制限のみです。つまり、指数の肩にある数字に注目すると個数制限 Nim(NimK などと呼ばれます) と言えるでしょう。
\(M = 24 = 2^3 × 3^1\) であれば、コインの山が 2 つあり、それぞれコインが3枚と1枚になっていると捉えることができます。
個数制限Nimの解き方
個数制限 Nim は、これもまた部分ゲームに分解して考えるとうまくいきます。(元々の不偏ゲームの、部分ゲームの部分ゲームなので、第2部分ゲームとでも呼びましょう。)
「1 個の山しか与えられなかった時の個数制限Nim」を並行して進めていると捉えると、スプレイグ・グランディの定理を再び以下のように適用することができます。
- 第1部分ゲーム(NimK)を第2部分ゲーム(「1 個の山しか与えられなかった時の NimK」)に分割する
- それぞれの第2部分ゲームに対して、その状況での Grundy数を計算する
- 計算したGrundy数全てに対しての XOR を取る
- XOR sum の値が、第1部分ゲームでの Grundy数になる
ではこの第2部分ゲームのGrundy数を求めてみましょう。以下のように左から順番に簡単に求めることができます。
| コインの枚数 n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| Grundy数 g(n) | 0 | 1 | 2 | 0 | 1 | 2 | 0 | … |
よく見ると、「Grundy数 = nを3で割った余り」というのが成り立っているのが分かります。
解法
スプレイグ・グランディの定理を2回適用することになります。
- N個の部分ゲームに分割して、それぞれGrundy数を以下のように求める
- \(M_i\)を素因数分解した時の肩の値をコインの枚数とした個数制限 Nim と見なし、Grundy数を以下のように求める
- 第1部分ゲームを、山が1つの時の第2部分ゲームに分割して、それぞれのGrundy数を求める(個数を3で割った余りになる)
- 求めた第2部分ゲームのGrundy数の XOR sum を、第1部分ゲームのGrundy数とする
- \(M_i\)を素因数分解した時の肩の値をコインの枚数とした個数制限 Nim と見なし、Grundy数を以下のように求める
- N個のXOR sum の値で判定する。
C++ での実装例
#include <bits/stdc++.h>
using namespace std;
/* prime_factor(n)
入力:整数 n
出力:nの素因数分解
計算量:O(√n)前後
*/
template <typename T>
map<T, T> prime_factor(T n) {
map<T, T> ret;
for (T i = 2; i * i <= n; i++) {
T tmp = 0;
while (n % i == 0) {
tmp++;
n /= i;
}
ret[i] = tmp;
}
if (n != 1) ret[n] = 1;
return ret;
}
int N;
int main() {
cin >> N;
vector<int> M(N);
for (int i = 0; i < N; i++) {
cin >> M.at(i);
}
vector<int> grundy(N); // 第1部分ゲームのGrundy数
for (int i = 0; i < N; i++) {
// 素因数分解
map<int, int> p_fac = prime_factor(M[i]);
// 肩の数を格納して NimK とみなす
vector<int> nimk;
for (auto p : p_fac) {
int num = p.second;
nimk.push_back(num);
}
// 第2部分ゲームの XOR sum を計算
int xor_sum = 0;
for (auto n : nimk) {
xor_sum ^= (n % 3); // 第2部分ゲームの Grundy数(i%3) の XOR sum
}
grundy[i] = xor_sum;
}
// 第1部分ゲームの XOR sum を計算
int xor_sum = 0;
for (auto g : grundy) {
xor_sum ^= g;
}
if (xor_sum == 0) { // 後手必勝
cout << "Bob" << endl;
} else { // 先手必勝
cout << "Alice" << endl;
}
return 0;
}
問題例:HackerRank Misère Nim
Nim の勝利条件を逆にする。つまり、先手と後手は、複数用意したコインの山から以下のルールで交互にコインを取り合い、先にコインを取れなくなったほうが勝ちとなる。(最後のコインを取ったほうが負け。)
- コインの山を一つ選んで、その山から一枚以上のコインを好きなだけ取る
考え方
勝利条件を逆にした Nim を Misere Nim(Misère Nim) と言います。Misere Nim は以下のように勝敗判定ができることが知られています。
n個のコインの山があり、\(s_1, s_2, s_3, \cdots, s_n\) のコインがあれば、
- 後手必勝:以下の状況の時
- \(s_i > 1\) となる \(i\) が存在して、XOR sum(\(s_1 \oplus s_2 \oplus s_3 \oplus … \oplus s_n\)) が0
- 全ての \(i\) について \(s_i \leq 1\) となり、XOR sum(\(s_1 \oplus s_2 \oplus s_3 \oplus … \oplus s_n\)) が1
- 先手必勝:上記以外の時
となります。
なぜ上述のように判定できるか
全ての山にあるコインの数が 1枚ずつであれば、先手と後手は交互に山を1つずつ減らすことになるので、山の数が奇数なら後手必勝・偶数なら先手必勝です。XOR sum(\(s_1 \oplus s_2 \oplus s_3 \oplus … \oplus s_n\))が 1なら奇数個、0なら偶数個と判定できます。
その他の状況では、通常のNim と同様に扱うことができます。
特に、「コインの数が1より大きい山 \(i\) が1つしか無い時」に注目すると分かりやすいでしょう。
- コインの数が1枚の山しか無い時:先手と後手は交互に山を1つずつ減らすことになるので、山の数が奇数なら後手必勝・偶数なら先手必勝です
- XOR sum が 0 なら偶数個の山 → 勝ち
- XOR sum が 1(non-zero) なら奇数個の山 → 負け
- コインの数が1より大きい山 \(i\) が1つしか無い時
- XOR sum が 0 になることはありません
- XOR sum が non-zero で必勝です。山 \(i\) のコインの数に由来します。この山から取って、コインを1つにするか、コインを0にするかを選ぶことができます。つまり、先程の「コインの数が1枚の山しか無い時」に変化させることができて、その山の数が偶数か奇数かを選ぶことができます。
- コインの数が1より大きい山が2つ以上ある時:いつか「コインの数が1より大きい山 \(i\) が1つしか無い時」にできます
- XOR sum が 0 なら、どのように取っても XOR sum は non-zero に変化してしまいます
- XOR sum が non-zero なら、上手く取ることで、XOR sum を0 にすることができます
C++ での実装例
#include <bits/stdc++.h>
using namespace std;
int T;
int main() {
cin >> T;
vector<bool> first_win(T);
for (int t = 0; t < T; t++) {
int n;
cin >> n;
vector<int> s(n);
for (int i = 0; i < n; i++) {
cin >> s.at(i);
}
bool overone = false; // 1より大きいものが存在するか
int xor_sum = 0;
for (int i = 0; i < n; i++) {
if (s[i] > 1) overone = true;
xor_sum ^= s[i];
}
if ((overone && xor_sum == 0) || (!overone && xor_sum == 1)) {
first_win[t] = false;
} else {
first_win[t] = true;
}
}
for (int t = 0; t < T; t++) {
if (first_win[t]) {
cout << "First" << endl;
} else {
cout << "Second" << endl;
}
}
}
練習問題
Nim
- yukicoder No.524 コインゲーム:Nimと分かっても計算するのに苦労するかもしれません。実験してみると性質が見えます。
スプレイグ・グランディの定理の適用
- [AtCoder] ARC 013 C 笑いをとれるかな?:複雑ですが部分ゲームに分解すれば分かりやすくなります。
- AOJ Playing With Stones:grundy数を動的計画法で前処理するか、メモ化再帰を使用しましょう。(実装例)
ディスカッション
コメント一覧
まだ、コメントがありません