ダブリングによる木の最近共通祖先（LCA：Lowest Common Ancestor）を求めるアルゴリズム
最近木においてある頂点の祖先は「親をたどってたどり着ける頂点」を指し、2頂点の共通祖先は「2頂点が共通して持つ祖先」のことを言います。
頂点 u と v の最近共通祖先(LCA: Lowest Common Ancestor) とは、「共通祖先の中でも、最も u, v に近い頂点」のことです。
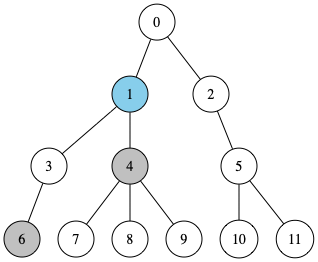
アルゴリズム
ダブリングによりLCAを求めるアルゴリズム：
- 前処理
- DFSなどによって、全ての頂点について、根からの距離と親を求める
- ダブリングによって \(2^k\) 先の祖先を求める
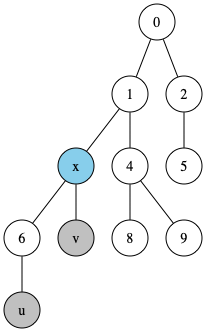
- クエリ（u と v の最近共通祖先 x を求める。）
- u と v の深い方の頂点を変更して「x までの距離が同じ点 u1, v1」にする
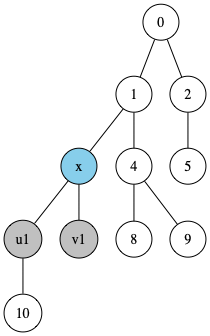
- 二分探索を用いて u1, v1 を最近共通祖先 x の一つ手前まで段階的に移動させる（u1, v1 が同じにならないギリギリまで移動させる）
- 最終的な u1, v1 の一つ先が LCA
※ x から先の頂点は全て「共通祖先」となるため二分探索が使用できますが、普通の二分探索のように、「dを決め打ちして、d先の頂点を実際に得ようとする」のは一回あたり\(O(logN)\)かかり、全体で\(O((logN)^2)\)の計算量になります。（つまり「条件 C(d)：u1 と v1 から d さかのぼった点は共通祖先か」を満たす最小の d を二分探索で見つけるような場合です。）
ですが \(k = 2^K, 2^{(K-1)}, 2^{(K-2)},… , 2^0\) について 「k個先を確認して共通祖先でないなら u1,v1 をk個先に移動」ということを繰り返すと、最終的に u1,v1 が LCA の直前になるまで移動させることができ、全体で\(O(logN)\)で求めることが可能です。
以上の話は実装例を見たほうが早いかもしれません。
※ u1, v1 の片方は、もともとの u, v と同じ頂点です。
※ダブリングについては、ダブリングの基本概念とその応用 を参照してください
計算量
- 前処理：\(O(N\log N)\) 時間, \(O(N \log N)\) 空間
- クエリ：\(O(\log N)\)
N 頂点あった時、一つの頂点あたり約 \(\log N\) 個の値を保持する必要があります。よって、時間計算量・区間計算量ともに \(O(N \log N)\) です。
C++ による実装例とまとめ
グラフ G と根 root を受け取って前処理を行い、LCA を二分探索で求めます。
struct Edge {
long long to;
};
using Graph = vector<vector<Edge>>;
/* LCA(G, root): 木 G に対する根を root として Lowest Common Ancestor を求める構造体
query(u,v): u と v の LCA を求める。計算量 O(logn)
前処理: O(nlogn)時間, O(nlogn)空間
*/
struct LCA {
vector<vector<int>> parent; // parent[k][u]:= u の 2^k 先の親
vector<int> dist; // root からの距離
LCA(const Graph &G, int root = 0) { init(G, root); }
// 初期化
void init(const Graph &G, int root = 0) {
int V = G.size();
int K = 1;
while ((1 << K) < V) K++;
parent.assign(K, vector<int>(V, -1));
dist.assign(V, -1);
dfs(G, root, -1, 0);
for (int k = 0; k + 1 < K; k++) {
for (int v = 0; v < V; v++) {
if (parent[k][v] < 0) {
parent[k + 1][v] = -1;
} else {
parent[k + 1][v] = parent[k][parent[k][v]];
}
}
}
}
// 根からの距離と1つ先の頂点を求める
void dfs(const Graph &G, int v, int p, int d) {
parent[0][v] = p;
dist[v] = d;
for (auto e : G[v]) {
if (e.to != p) dfs(G, e.to, v, d + 1);
}
}
int query(int u, int v) {
if (dist[u] < dist[v]) swap(u, v); // u の方が深いとする
int K = parent.size();
// LCA までの距離を同じにする
for (int k = 0; k < K; k++) {
if ((dist[u] - dist[v]) >> k & 1) {
u = parent[k][u];
}
}
// 二分探索で LCA を求める
if (u == v) return u;
for (int k = K - 1; k >= 0; k--) {
if (parent[k][u] != parent[k][v]) {
u = parent[k][u];
v = parent[k][v];
}
}
return parent[0][u];
}
};
アルゴリズムの説明
ダブリングとは
ダブリングは全体の要素数がN個のとき「K個先の要素を求めるのに \(O(K)\) かかる」ような状況を
- 前処理：\(O(N \log K)\) 時間, \(O(N \log K)\) 空間
- クエリ：\(O(\log K)\)
で行うことができるようにするアルゴリズムです。
実現のためには以下のようにします。
- 前処理
- それぞれの要素について 1 個先の要素が何か記録
- 前の結果を利用して、それぞれの要素について 2 個先の要素が何か記録
- 前の結果を利用して、それぞれの要素について 4 個先の要素が何か記録
- 前の結果を利用して、それぞれの要素について 8 個先の要素が何か記録
- 前の結果を利用して、それぞれの要素について 16 個先の要素が何か記録
- …
- クエリ：二分探索や繰り返し二乗法と同様の方法で K 個先の要素が何か探索
\(2^k\) 先の要素が分かっていれば「 “\(2^k\) 先の要素" の\(2^k\) 先」を簡単に求めることができるので、「\(2^{k+1}\) 先の要素が何か」を高速に求めることができます。
LCAをダブリング求めるアイディア
根から頂点 v への距離を dist(v) と書くことにします。頂点 u, v の LCA が x だった場合、以下が成り立つはずです。
- u から dist(u)-dist(x) 回 だけ根へさかのぼった時の点が x
- v から dist(v)-dist(x) 回 だけ根へさかのぼった時の点が x
このままではダブリングが使えません。そこで以下のように「x までの距離が同じ点 u1, v1」を用意します。簡単のために u の方がより深い点としましょう。つまり dist(u)>dist(v) です。
- u から |dist(u)-dist(v)| 回 さかのぼった点を u1 とする
- u1 から「 dist(v) – dist(x) 」回さかのぼった点が x
- v を v1 とする
- v1 から 「dist(v) – dist(x)」 回さかのぼった点が x
こうすると、「u1 と v1 からある距離（dist(v) – dist(x)）以上の距離 d だけさかのぼると同じ頂点になる」と言えます（最近共通祖先から先の祖先は全て共通祖先です）。
このようにすると、二分探索を利用することができて、二分探索を用いて u1, v1 を最近共通祖先 x の一つ手前まで段階的に移動させる（u1, v1 が同じにならないギリギリまで移動させる）ようにすれば良いです。
応用
LCA で 任意の2頂点間の距離が分かる
LCA の計算過程で、根からの距離を全ての頂点について計算済みです。
頂点 u, v の LCA が x だった場合、
- dist(u) + dist(v) – 2 × dist(x)
で u, v 間の距離を求めることができます。
int get_dist(int u, int v) { return dist[u] + dist[v] - 2 * dist[query(u, v)]; }
パス上にある頂点があるか分かる
頂点 u, v を結ぶパス上に、ある頂点 a が存在するかも簡単に判定ができます。
頂点 a がパス上にあれば
- u と a の距離 + a と v の距離
- u と v の距離
が等しくなります。逆に等しくなければパス上にはありません。
bool is_on_path(int u, int v, int a) { return get_dist(u, a) + get_dist(a, v) == get_dist(u, v); }