グラフ(Graph)のデータ構造と基本用語の定義
グラフとは
頂点(ノード)と、頂点同士の関係を表したデータ構造です。
数学的には、グラフは以下の2つから構成されます。
- 頂点(ノード)の集合
- 頂点同士がつながっているか(隣接しているか)を表す、辺(エッジ)の集合
もう少し厳密に書くと、グラフ\(G\)というのは、ノードの集合\(V\)とエッジの集合\(E(\subset V \times V)\)を用いて、$$G=\{V, E\}$$と表すことができます。
\(V\)はvertices(頂点)の頭文字、\(E\)はedges(辺)の頭文字なので、これらの文字が使われることが多いです。
具体例
頂点の集合が\(V=\{0,1,2,3\}\)、辺の集合が\(E=\{(0,1),(0,2),(2,1),(1,3),(2,3)\}\)となるグラフは以下のようになります。
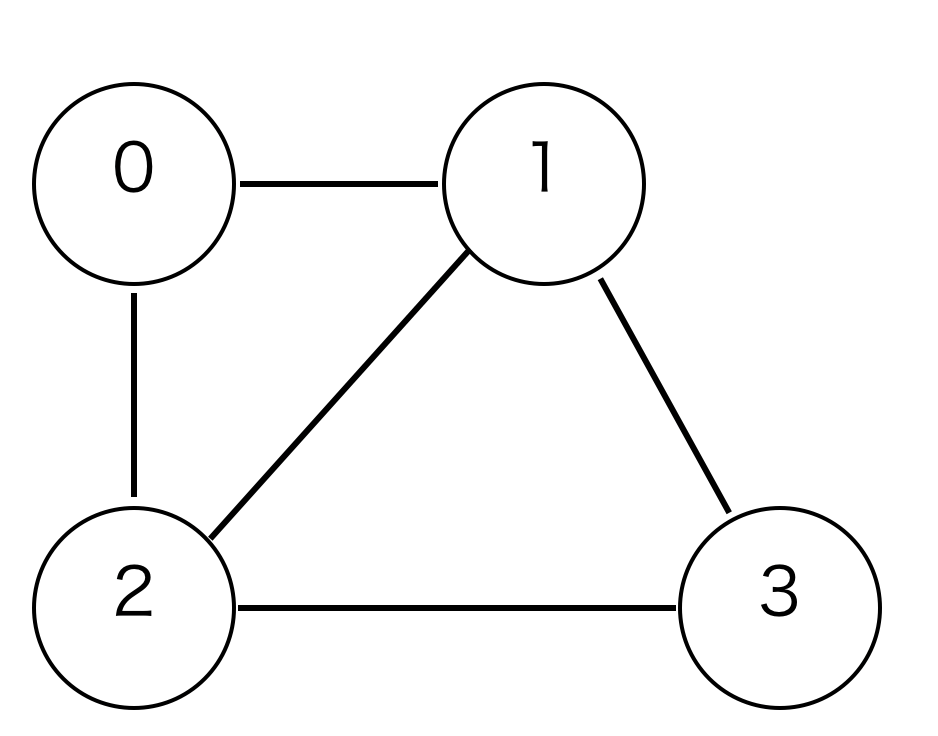
有向グラフと無向グラフ
グラフは辺に向きがあるかどうかで2種類に分けられます。
- エッジに向きがある有向グラフ
- エッジに向きがない無向グラフ
先程までの例は無向グラフの例でした。
\(V=\{0,1,2,3\}\)、\(E=\{(0,1),(0,2),(2,1),(1,3),(2,3)\}\)の有向グラフでは以下のようになります。
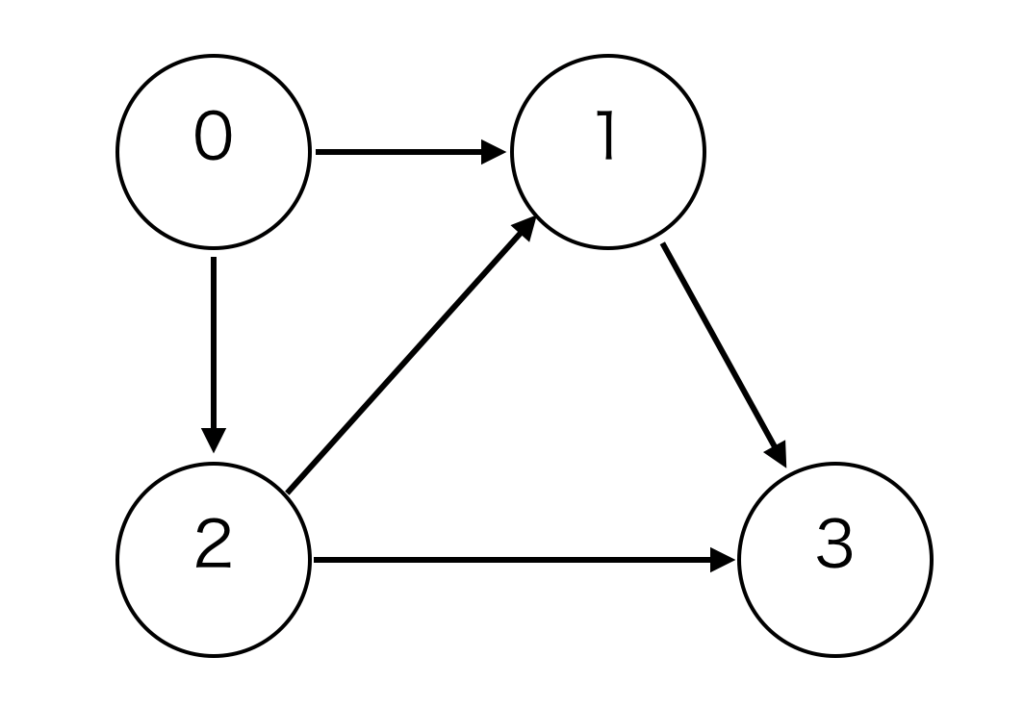
今回のように\((0,2) \in E\)となっている時は、頂点0から頂点2への辺となります。逆に、\((2,0) \in E\)の時は逆向きの辺になります。
重み付きグラフ
辺に重み(コスト)がついているグラフを重み付きグラフと言います。辺に重みをつけることで、頂点間の移動にかかる時間やコストなどを表現することができます。
以下は重み付きの無向グラフの一例です。
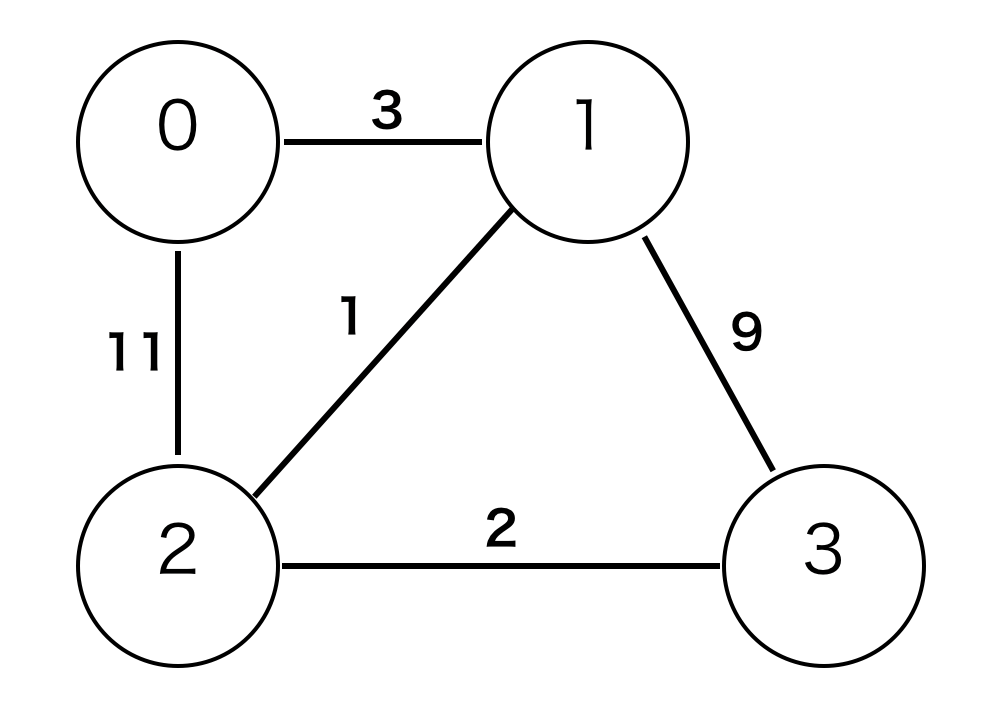
グラフでの基本用語
グラフの性質を簡単に表現するために、様々な用語が使われます。とくに
隣接と接続
頂点同士が辺で繋がっていることを、「隣接している」と言います。先程の例で言えば、\((0,2) \in E\)となっているので、頂点0と頂点2は隣接しています。
また、頂点とエッジが繋がっていることを、「接続している」と言います。
道(path)
2つの頂点同士を繋ぐ経路(通る辺と頂点の列)のことを「道(path)」と言います。
特に「単純道(single path)」は、通る頂点が全て異なる「道」のことを言います。
閉路
始点と終点が同じで、それ以外の通った頂点が全て異なる歩道のことを「閉路(cycle)」と言います。
連結と非連結
「連結」とは任意の2頂点間を行き来できることを言い、「非連結」は逆に行き来できない頂点があることを言います。
連結なグラフは「連結グラフ」などと言います。
強連結
有向グラフにおいて、任意の2頂点間を行き来できる時は、「強連結」と言います。
グラフの実装方法
様々なものをグラフと捉えることが可能なので、グラフを使用する機会は多いです。グラフの実装方法としては、隣接行列を用いた方法と、隣接リストを用いた方法があります。
隣接行列
行列を用いたグラフの表現方法です。頂点\(i\)から頂点\(j\)への辺がある時、\(i\)行目と\(j\)列目の要素を1とします。逆に、隣接していない時は0とします。
無向グラフのときは、頂点\(i\)から頂点\(j\)への辺がある時、\(i\)行目と\(j\)列目、\(j\)行目と\(i\)列目の両方の要素を1とします。
重み付きグラフの場合は、1ではなく重み(コスト)とします。
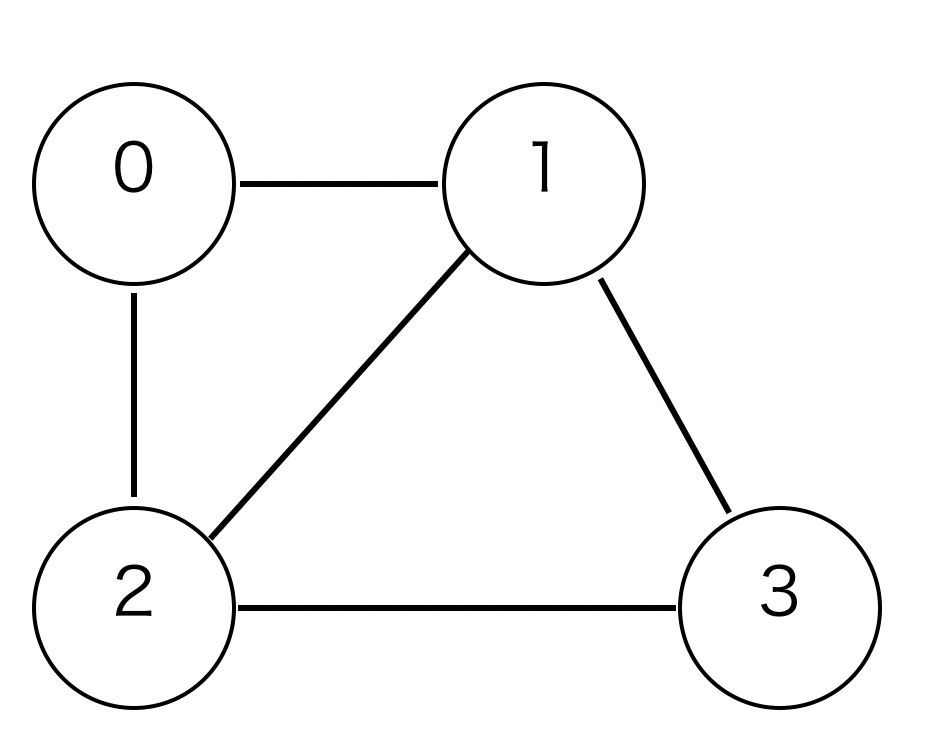
無向グラフの例
頂点が4つあるので、4行4列の行列で表すことができます。無向グラフなので、行列は対称行列となります。
$$\left(\begin{array}{ccc}
0 & 1 & 1 & 0 \\
1 & 0 & 1 & 0 \\
1 & 1 & 0 & 1 \\
0 & 1 & 1 & 0
\end{array} \right)$$
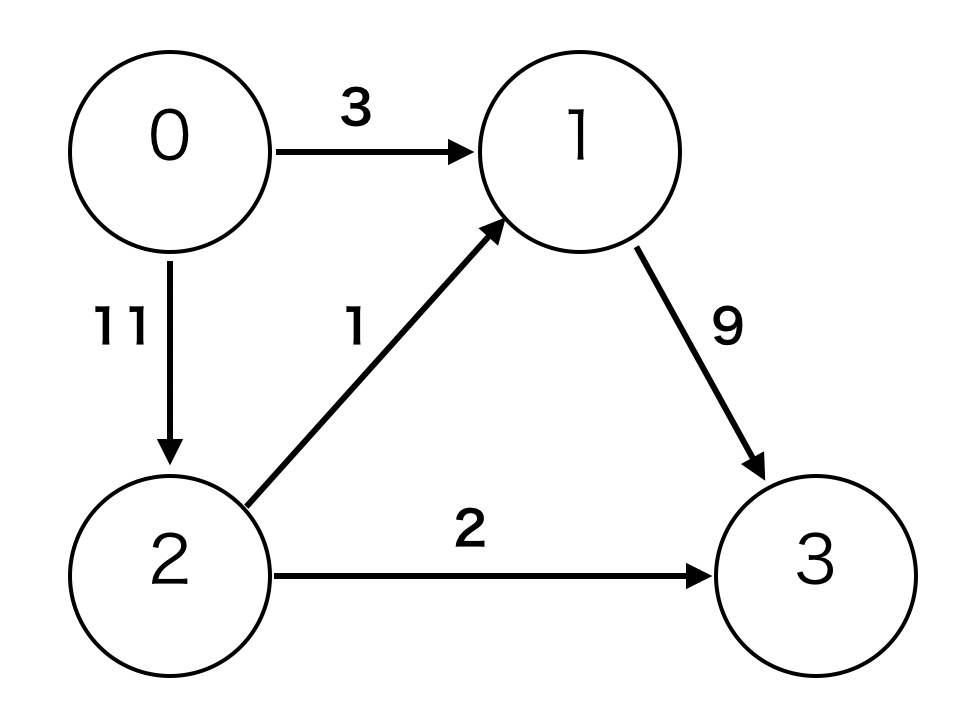
重み付き有向グラフの例
先程と同様に4行4列の行列ですが、有向グラフなので対称行列とはならず、要素も辺のコストを使用します。辺が無い時は、重みが0の時と区別できるように\(\infty\)などとします。
$$\left(\begin{array}{ccc}
\infty & 3 & 11 & \infty \\
\infty & \infty& \infty& 9 \\
\infty & 1 & \infty & 2 \\
\infty & \infty& \infty & \infty
\end{array} \right)$$
隣接リスト
各頂点ごとに、どの頂点と繋がっているのかのリストを保持するのが、隣接リストです。
さきほどの隣接行列では、頂点数を\(n\)とした時にメモリの使用量が\(O(n^2)\)の大きさになってしまいます。隣接リストでは、辺の数が少ない(行列がスパースな)時にメモリの使用量が少なくなるという利点があります。

無向グラフの例
1つの辺に対して、2つの頂点があるので、無向グラフではそれぞれの頂点に対して、情報をリストとして保持します。
| 頂点 | リスト |
| 0 | 1,2 |
| 1 | 0,2,3 |
| 2 | 0,1,3 |
| 3 | 0,1,2 |
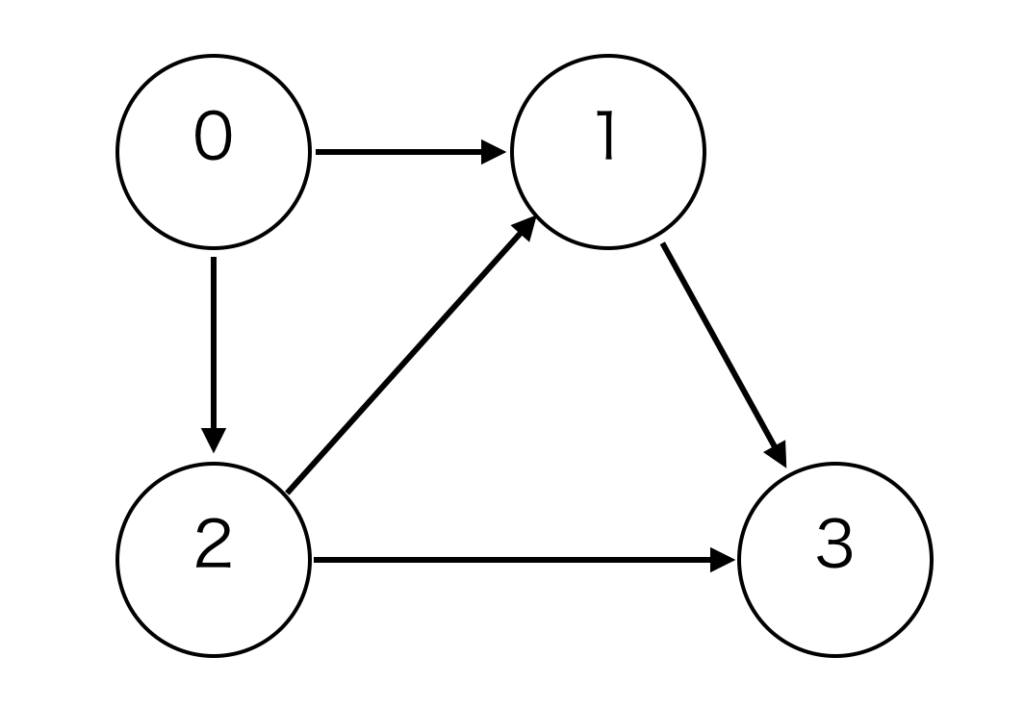
有向グラフの例
有向グラフでは、自身から出ている辺の終点となる頂点をリストとして保持します。
| 頂点 | リスト |
| 0 | 1,2 |
| 1 | 3 |
| 2 | 1,3 |
| 3 | なし |
ディスカッション
コメント一覧
グラフの実装方法節の、隣接リスト節の、無向グラフの例の表の、頂点3に対応するリストは1,2だと思います