ダイクストラ法による単一始点最短経路を求めるアルゴリズム

2020年3月7日グラフグラフ,競プロ,重み付きグラフ,単一始点最短経路,最短経路,ダイクストラ法,ヒープ,優先度付きキュー,貪欲法

グラフにおける単一始点最短経路問題とは、始点を固定した時に、他のすべての頂点への最短経路を求める問題のことです。

ダイクストラ法は、単一始点最短経路問題を解く時に利用され、利点としては

  • 計算量が \(O(|E| \log |V|)\) であり、ベルマンフォード法の計算量 \(O(|E|×|V|)\) よりも高速に動作する

というのが挙げられます。一方で、欠点として

  • 負の辺があるときに使用できない

というのがありますが、最短経路を求める非常に有名なアルゴリズムの一つです。

アルゴリズム

ダイクストラ法：

  1. 始点 s を「既に最短距離が確定した頂点」、他の頂点を「まだ最短距離が確定していない頂点」とする
  2. 以下をすべての頂点の最短距離が確定するまで繰り返す
    1. 全ての「既に最短距離が確定した頂点 u 」から「まだ最短距離が確定していない頂点 v 」へ伸びる全ての辺 e=(u,v) について、「v と d[v] の候補」をまとめておく
    2. 候補の中から、d[v] が最小のものを選択し、v を「既に最短距離が確定した頂点」に加える

※ 頂点集合を V・辺の集合を E とした、グラフ G=(V,E) において、始点 s から 頂点 v への最短距離を d[v] としています。

※ ダイクストラ法は、行ける場所の中から「最も早く行ける場所」を順番に確定させていきます。

頂点 1, 2, 3 の中から最短で行ける場所を探す
頂点 2 へ最短で行けるため確定

計算量

  • ヒープを使わない場合：
    • \(O(|V|^2)\)
  • ヒープを使う時：
    • \(O(|E| \log |V|)\)

候補の中から d[v] が最小のものを選択するには、単純にやると全ての候補を確認することになるので \(O(|V|)\) の計算量がかかってしまいます。これを頂点数だけ繰り返すので、この場合の計算量は \(O(|V|^2)\) です。

しかし、ヒープなどのデータ構造を上手く使うと候補の追加や最小値の取得が \(O(\log |V|)\) で計算できます。この時の、更新と取り出しの回数は辺の数だけ生じるので \(O(|E|)\) です。

\(|E|\) が小さければ、後者の方が高速に動きます。

C++での実装例

ヒープを利用した時の実装例です。

C++ では STL の priority_queue をヒープとして利用することができます。

以下の実装では、仮の「頂点と最短距離」を全て priority_queue に入れているので、\(O(|E| \log |E|)\) の計算量になりそうですが、最短距離でない場合は無視をすることで、\(O(|E| \log |V|)\) になっています。（いずれにせよ \(\log |E| \leq \log |V|^2 = 2 \log |V|\) から同じ計算量になります。）

#include <bits/stdc++.h>
using namespace std;

struct Edge {
    long long to;
    long long cost;
};
using Graph = vector<vector<Edge>>;
using P = pair<long, int>;
const long long INF = 1LL << 60;

/* dijkstra(G,s,dis)
    入力：グラフ G, 開始点 s, 距離を格納する dis
    計算量：O(|E|log|V|)
    副作用：dis が書き換えられる
*/
void dijkstra(const Graph &G, int s, vector<long long> &dis) {
    int N = G.size();
    dis.resize(N, INF);
    priority_queue<P, vector<P>, greater<P>> pq;  // 「仮の最短距離, 頂点」が小さい順に並ぶ
    dis[s] = 0;
    pq.emplace(dis[s], s);
    while (!pq.empty()) {
        P p = pq.top();
        pq.pop();
        int v = p.second;
        if (dis[v] < p.first) {  // 最短距離で無ければ無視
            continue;
        }
        for (auto &e : G[v]) {
            if (dis[e.to] > dis[v] + e.cost) {  // 最短距離候補なら priority_queue に追加
                dis[e.to] = dis[v] + e.cost;
                pq.emplace(dis[e.to], e.to);
            }
        }
    }
}

最短距離の経路復元

ダイクストラ法で最短距離を求めるついでに、「1つ前にどの頂点を通ったか」を記録しておけば、終点から逆にたどっていくことで、最短距離の経路を復元することができます。

先程の関数を少し拡張すると以下のようになります。prev という vector に「1つ前にどの頂点を通ったか」記録しています。

/* dijkstra(G,s,dis,prev)
    入力：グラフ G, 開始点 s, 距離を格納する dis, 最短経路の前の点を記録するprev
    計算量：O(|E|log|V|)
    副作用：dis, prevが書き換えられる
*/
void dijkstra(const Graph &G, int s, vector<long long> &dis, vector<int> &prev) {
    int N = G.size();
    dis.resize(N, INF);
    prev.resize(N, -1); // 初期化
    priority_queue<P, vector<P>, greater<P>> pq; 
    dis[s] = 0;
    pq.emplace(dis[s], s);
    while (!pq.empty()) {
        P p = pq.top();
        pq.pop();
        int v = p.second;
        if (dis[v] < p.first) {
            continue;
        }
        for (auto &e : G[v]) {
            if (dis[e.to] > dis[v] + e.cost) {
                dis[e.to] = dis[v] + e.cost;
                prev[e.to] = v; // 頂点 v を通って e.to にたどり着いた
                pq.emplace(dis[e.to], e.to);
            }
        }
    }
}

記録した点を用いて、後ろから始点 r へとたどっていくことで経路を復元することができます。

/* get_path(prev, t)
    入力：dijkstra で得た prev, ゴール t
    出力： t への最短路のパス
*/
vector<int> get_path(const vector<int> &prev, int t) {
    vector<int> path;
    for (int cur = t; cur != -1; cur = prev[cur]) {
        path.push_back(cur);
    }
    reverse(path.begin(), path.end()); // 逆順なのでひっくり返す
    return path;
}

アルゴリズムの考え方と正当性

基本となる式と考え方

頂点集合を V・辺の集合を E とした、グラフ G=(V,E) において、始点 s から 頂点 t への最短距離を d[t] と表すことにします。

基本はベルマンフォード法と同じく以下の式が成立することを利用します。

  • d[v] = min{ d[u] + ( 辺e=(u,v) の距離 ) }

この式を利用して、最短距離を始点 s に近い頂点から順番に決定していくことができれば、すべての頂点に対して最短距離を求めることが可能です。

最短距離を1つずつ確定させていく

ベルマンフォード法での問題点は何かというと、「ある頂点までの最短距離が求まったかどうか最後まで分からない」というところにありました。

しかし、「負の辺が存在しない」という仮定を入れると、「最短距離が求まった頂点」を順番に決定していくことができます。

ダイクストラ法では、最短距離を以下のように確定させていきます。

  1. 「最短距離が確定した点集合」とつながる頂点について、最短距離 d[i] の候補をまとめておく
  2. 候補の中から、最もd[i] が小さい頂点を「最短経路が確定した点集合」に加える

具体例で確認

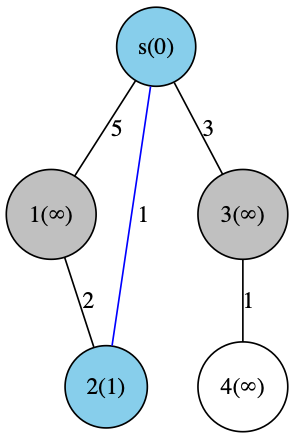
先程の手順を具体例で確認してみましょう。

「最短距離が求まった頂点」を水色・「まだ最短距離が確定していない点」のうち水色のものと繋がっているものを灰色で表すことにします。

始点のみが最短距離が確定

灰色のノードが、次に更新されるノードの候補です。

  • s→2：d[2] = 1
  • s→3：d[3] = 3
  • s→1：d[1] = 5

という候補があるので、この中から距離が最小のものを選びます。

s と 2 の間の辺のコストが最小

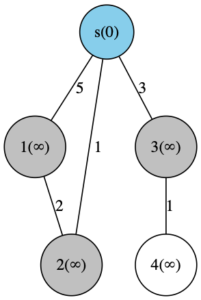
これで、s と 2 が「最短距離が確定した頂点」になりました。次の候補としては、

  • s→2→1：d[1] = 1+2 = 3
  • （s→1：d[1] = 5）
  • s→3：d[3]= 3

があり、この中から距離が最小のものを選択します。（d[1]に関してはより距離が小さい方を残します。）

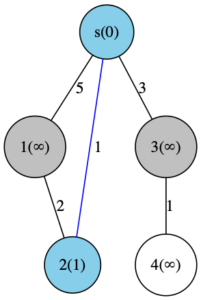
あとの候補の残りは以下1つだけです。

  • s→3：d[3]= 3

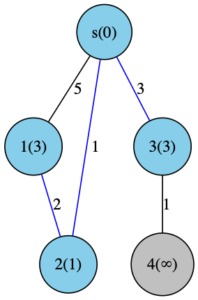
3が確定した頂点になったので、4を灰色に変更しました。

あとの候補の残りは以下の通りです。

  • s→3→4：d[4] = 3+1 = 4

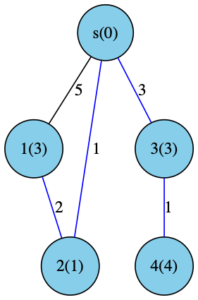
これで終了です。これ以上頂点が更新されることはありません。

以上で見たように、「最短距離が小さいもの」から順番に頂点を確定させていくことができます。これは、「負の辺が存在しない」という仮定があったからできることです。

練習問題

グラフグラフ,競プロ,重み付きグラフ,単一始点最短経路,最短経路,ダイクストラ法,ヒープ,優先度付きキュー,貪欲法