木の直径を求めるアルゴリズム
木に存在する2つノード間の最大距離を木の直径と言います。
重み無しの木でも、重み付きの木でも、木の最遠頂点間の距離が直径になります。
重み無しの木の例:
以下は直径が5となる木の例です。
6-3-1-0-2-5 を結ぶパスを見ると頂点数は6つで距離は 5 になっています。
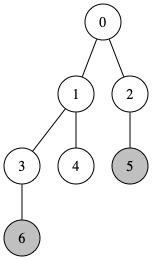
※ 木の2つの葉(末端にある頂点)を結ぶパス中に含まれる頂点数で最大の数を木の直径とする場合もあります。 上の図では 6 となります。
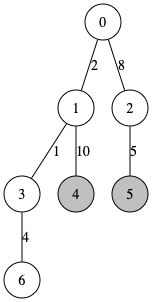
重み付きの木の例:
以下の重み付き木の場合は、4-1-0-2-5 を結ぶパスの距離で 25 になっています。
アルゴリズム
※ 辺の重みを全て 1 とすれば、重み無し木の直径を求めることになります。
※ 「どの頂点から始めても、最も遠くにある頂点 x は直径の端点になる」という事実を利用しています。
計算量
- \(O(N)\)
頂点数を N とした時を考えます。木の辺の数は N-1 なので、DFSまたはBFSには \(O(N)\) だけかかります。この探索を2回行うので、全体としては \(O(N)\)です。
C++ での実装例
template <typename T>
struct Edge {
int to;
T cost;
};
using Graph = vector<vector<Edge<long long>>>; // cost の型を long long に指定
/* tree_diamiter : dfs を用いて重み付き木 T の直径を求める
計算量: O(N)
*/
template <typename T>
pair<T, int> dfs(const Graph &G, int u, int par) { // 最遠点間距離と最遠点を求める
pair<T, int> ret = make_pair((T)0, u);
for (auto e : G[u]) {
if (e.to == par) continue;
auto next = dfs<T>(G, e.to, u);
next.first += e.cost;
ret = max(ret, next);
}
return ret;
}
template <typename T>
T tree_diamiter(const Graph &G) {
pair<T, int> p = dfs<T>(G, 0, -1);
pair<T, int> q = dfs<T>(G, p.second, -1);
return q.first;
}
アルゴリズムの正当性
このアルゴリズムの重要なポイントは以下の事実です。
- どの頂点から始めても、最も遠くにある頂点 x は直径の端点になる
これが成立すれば、適当な頂点 s に対して最も遠くにある点 u は直径の一方の端点になり、u に対して最も遠くにある点 v はもう一方の端点になるはずです。
以下で簡単な証明をしますが、難しければ飛ばしても構いません。
背理法で証明
厳密ではありませんが、簡単に証明を考えてみましょう。
「根 r から最も遠くにある頂点 x は直径の端点にならない」と仮定して矛盾を示すことを考えます。直径の端点をu, v とします。rからx へのパスが直径と最初に交わる点が存在すればそれを h とします。
- h が存在する時
- 「r → h → x 」となるパスがあります。この時 h から最も遠くにある点を考えると h は直径上にあるので本来は u or v になるはずです。しかし「根 r から最も遠くにある頂点は x 」なので x は u または v となってしまい矛盾が生じます。
- h が存在しない時
- u から v への直径上にある点を h’ としましょう。$$dist(r, h’) + dist(h’, x) \geq dist(r, x) $$ であることに注意すると、
\begin{align}
dist(r, x) &\geq dist(r, h’) + \max( dist(u, h’), dist(v, h’)) \\
\Rightarrow dist(h’, x) &\geq \max( dist(u, h’), dist(v, h’))
\end{align}
以上の式から、xを端点とする直径を構成することができるので矛盾が生じます。
- u から v への直径上にある点を h’ としましょう。$$dist(r, h’) + dist(h’, x) \geq dist(r, x) $$ であることに注意すると、
練習問題
- AOJ GRL_5_A Diameter of a Tree
- [AtCoder] ABC 019 D – 高橋くんと木の直径:インタラクティブ形式の問題です。木の直径を求めるアルゴリズムを理解していれば分かるはずです
- [AtCoder] AGC 033 C – Removing Coins:直径が関係すると気がつくまでが難しいです
ディスカッション
コメント一覧
まだ、コメントがありません