重みが最小となる閉路を求めるアルゴリズム
アルゴリズム
最小コストの閉路:
- 任意の辺 e = (u,v) について以下を繰り返す
- グラフ G から e を取り除く
- v から u への最短経路 d を求める(ダイクストラ/BFS など)
- d+cost(u,v) を計算する
- グラフ G に e を戻す
- d+cost(u,v) の最小値が、閉路の重みの最小値
※ ある辺 e を含む最小のコストの閉路を、全ての辺について求めます。
※ 具体例では以下の様になります。
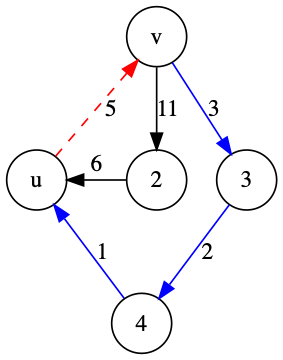
辺 e = (u,v) が使われる閉路のうち、重みが最小となるものは右図のようになります。
e を取り除いたグラフにおいて、u→*vの最短経路は
- d = 3+2+1 = 6
となり、閉路の最小コストは
- d+cost(u,v) = 6 + 5 = 11
です。
※ このアルゴリズムは無向グラフ・有向グラフの両方に対して使用できます。
※ 重みなしグラフの場合は、辺の重みを 1 として同様のアルゴリズムで求めることができます。
※ コストだけではなく、閉路そのものを求める場合は、経路復元を行えば良いです(ダイクストラ法を参照)。
計算量
- 重み付きグラフ(負の辺あり)の場合: \(O(E(EV))\)
- 重み付きグラフ(負の辺なし)の場合: \(O(E(E \log V))\)
- 重みなしグラフの場合: \(O(E(E + V))\)
最短経路を求めるアルゴリズムによって計算量が異なります。
コストが負の辺が含まれている場合は、ベルマンフォード法などを用いる必要があるので、最短距離を求めるのに一回あたり \(O(EV)\) だけかかります。
負の辺が含まれていない場合は、ダイクストラ法を用いることができるので、一回あたり \(O(E \log V)\) となります。
重みなしグラフの場合は、幅優先探索(BFS) で最短距離を \(O(E+V)\) で求めることが可能です。
実装例
以下は最短距離を求めるのにダイクストラ法を用いた場合の実装例です。
#include <bits/stdc++.h>
using namespace std;
template <typename T>
struct Edge {
int to;
T cost;
};
using Graph = vector<vector<Edge<long long>>>; // 距離/コストの型 T を指定する
const long long INF = (1LL << 60); // 型 T のINF
/* dijkstra(G,s,dis,prev)
入力:グラフ G, 開始点 s, 距離を格納する dis, 最短経路の前の点を記録するprev
計算量:O(|E|log|V|)
副作用:dis, prevが書き換えられる
*/
template <typename T>
void dijkstra(const Graph &G, int s, vector<T> &dis, vector<int> &prev) {
using P = pair<T, int>;
int N = G.size();
dis.resize(N, INF);
prev.resize(N, -1);
priority_queue<P, vector<P>, greater<P>> pq; // the least element is top. first:cost, second: node
dis[s] = 0;
pq.emplace(dis[s], s);
while (!pq.empty()) {
P p = pq.top(); // the least element
pq.pop();
int v = p.second;
if (dis[v] < p.first) {
continue;
}
for (auto &e : G[v]) {
if (dis[e.to] > dis[v] + e.cost) {
dis[e.to] = dis[v] + e.cost;
prev[e.to] = v;
pq.emplace(dis[e.to], e.to);
}
}
}
}
/* get_path(pre, t)
入力:得た pre, ゴール t
出力: t への最短路のパス
*/
vector<int> get_path(const vector<int> &pre, int t) {
vector<int> path;
for (int cur = t; cur != -1; cur = pre[cur]) {
path.push_back(cur);
}
reverse(path.begin(), path.end());
return path;
}
vector<int> min_cycle; // 最小の閉路に含まれる頂点
/* minimum_weight_cycle
出力:閉路の重みの最小値、閉路がなければ INF
最小の閉路に含まれる頂点は min_cycleに格納される
計算量:
重み付きグラフ(ダイクストラ法): O(EElogV)
*/
template <typename T>
T minimum_weight_cycle(Graph &G) {
int V = (int)G.size();
T ans = INF;
for (int v = 0; v < V; v++) {
for (int i = 0; i < (int)G[v].size(); i++) {
Edge<T> e = G[v][i];
G[v].erase(G[v].begin() + i); // e を消す
vector<T> dist;
vector<int> pre;
dijkstra<T>(G, e.to, dist, pre); // 最短距離を求める
if (ans > dist[v] + e.cost) {
ans = dist[v] + e.cost;
min_cycle = get_path(pre, v);
}
G[v].insert((G[v].begin() + i), e); // e を戻す
}
}
return ans;
}
練習問題
- [AtCoder] ABC 142 F – Pure:重みが無い場合なのでBFSで最短距離が求まりますが、高速な言語ならダイクストラ法でも間に合います
ディスカッション
コメント一覧
まだ、コメントがありません