深さ優先探索(Depth First Search)の基本
深さ優先探索とは、全探索アルゴリズムの一種です。グラフや、グラフと同一視できるものを探索する際に良く使われます。
幅優先探索(BFS)と似ていますが、深さ優先探索は末端に到達するまで「深く」探索してから、他のノードの探索を始めます。
英語では Depth First Search なので、DFSと略されることが多いです。
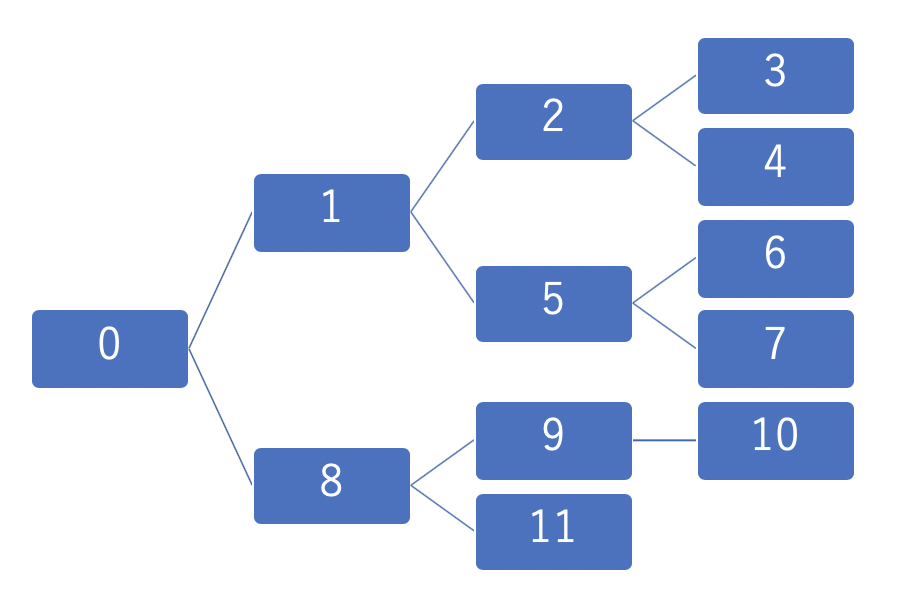
DFSのアルゴリズム
深さ優先探索は、「とりあえずこれ以上進めなくなるまで探索したら、戻って別のルートで探索し直す」ようなアルゴリズムです。
実装方法としては、主に二種類あり、
- スタックと呼ばれるデータ構造を用いた方法
- 再帰関数を用いた方法
があります。
スタックを用いたアルゴリズム:
- 始めの状態から遷移可能な状態を、全てスタックに入れる
- スタックに要素がなければ終了する
- 現在の状態から遷移可能な状態を、全てスタックに入れる
- スタックから1つ要素を取り出し、そこに状態を遷移させる
- 2.に戻る
※ 今まで通った場所をスタックに保存しながら進み、末端に到達したらスタックからどこに戻るかの情報を取出します。
※ 幅優先探索のアルゴリズムのうち、キューをスタックに変更しただけで実装できます。
※ 途中の状態は以下のようになります。
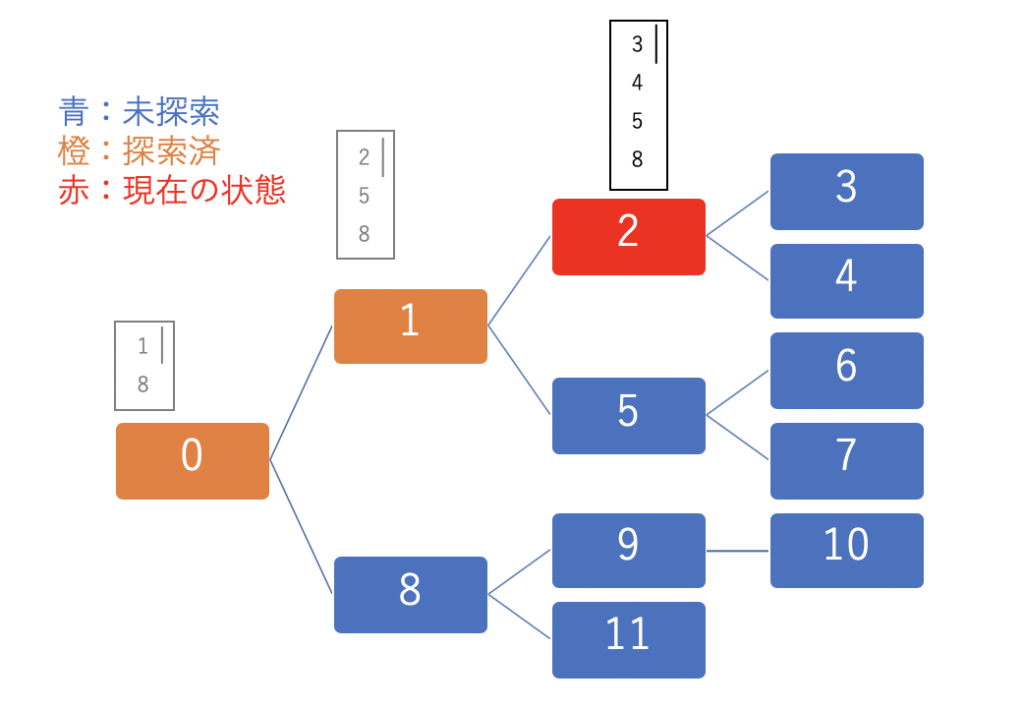
再帰関数を用いたアルゴリズム:dfs(u)
- 現在探索中の頂点 u を「探索済み」として記録しておく
- u と隣接している頂点のうち、「未探索」の頂点 v について以下を行う
- dfs(v) によって v を探索する
※ 再帰関数を用いて深さ優先探索を実装できます。遷移可能な状態の個数分だけ、再帰関数を呼出して分岐させていきます。コンピュータ内部で関数を使う際に、スタックにデータを保存しておくため、先ほどと同様の動作になります。
※ プログラムは上から下へ実行されるため、再帰関数の呼び出され方がスタックを用いた時と同じ様になります。遷移可能な状態が無くなる(末端にたどり着く)まで、戻って別のノードを探索することはありません。
※ 先程の図でいうと、状態1の時には、「状態2へ分岐する再帰関数」と「状態5へ分岐する再帰関数」を呼び出します。プログラムは上から下へ実行されるので、「状態2へ分岐する再帰関数」が先に実行され、これが終了するまで「状態5へ分岐する再帰関数」が呼び出されることはありません。
※DFSの応用例としては、 DFSによる全探索があります。DFSによって複雑な条件下での全探索をきれいに実装することができます。
計算量
- O(V+E)
グラフ \(G=(V,E)\) を深さ優先探索する場合は、(状況にもよりますが)全ての頂点と辺を走査することになるので、計算量は O(V+E) になります。
スタックと再帰関数のどちらが良いか
スタックを用いると幅優先探索と同様に書けるというメリットがあり、逆に再帰関数を用いると簡単に実装することができるというメリットがあります。
また、再帰関数は再帰が深くなるとスタックオーバーフローになる可能性があるので注意が必要です。
状況に合わせて、もしくは自分の好みで、どちらで実装するかを決めれば良いでしょう。
問題1:DFSで同じ連結成分にあるか判定する(グラフ)
頂点数 V 、辺の数 E のグラフについて、頂点 s から頂点 t に到達できるかを探索するプログラムを書いてみましょう。到達できれば 'yes’ と出力し、到達できなければ 'no’ と出力します。
入力形式
V, E, s, t に加えて、ai から bi への有向辺が E 個与えられます。
V E
s t
a1 b1
a2 b2
…
aE bE
入出力例
入力:
4 5
0 3
0 1
0 2
1 3
2 1
2 3
出力:
yes
この入力例では以下のようなグラフになります。
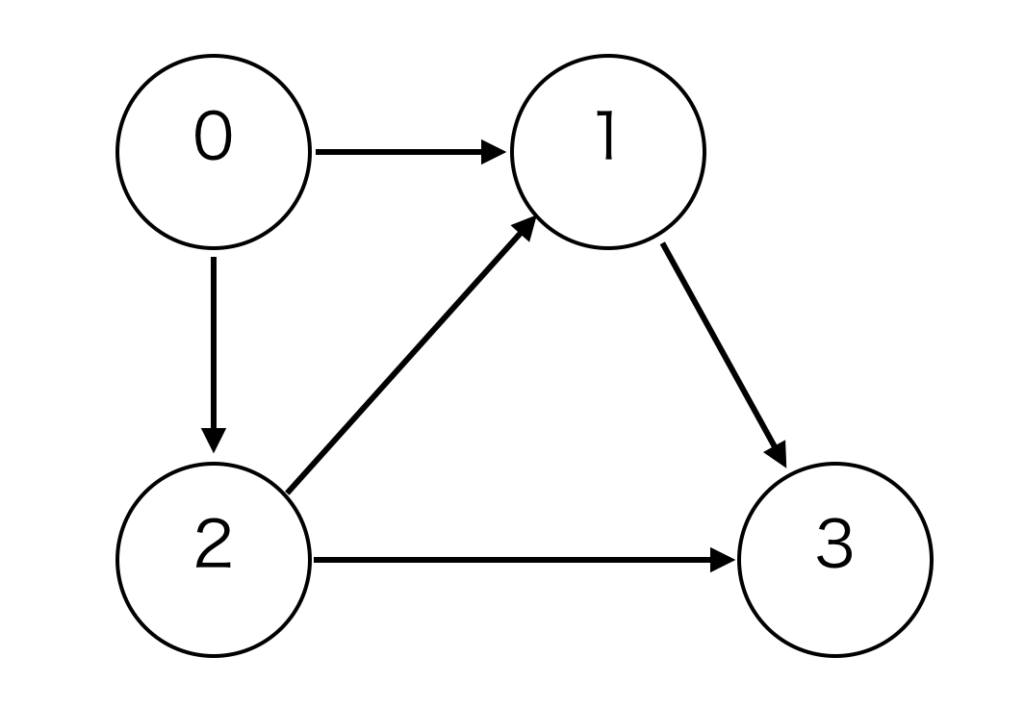
0からスタートして、3にたどり着ければ 「yes」、たどり着けなければ「no」を返します。この場合はたどり着けるので yes となります。
隣接行列・隣接リスト(グラフを参照)のどちらでグラフを表現するのか、スタック・再帰関数のどちらで深さ優先探索を実装するのかで、やり方が色々と変わってきます。
C++ での実装例
隣接リスト表現を用いて、スタックで実装すると以下のようになります。
#include <bits/stdc++.h>
using namespace std;
int main() {
int V, E;
cin >> V >> E;
int s, t;
cin >> s >> t;
vector<vector<int>> G(V);
for (int i = 0; i < E; i++) {
int a, b;
cin >> a >> b;
G[a].push_back({b});
// G[b].push_back({a});
}
vector<bool> seen(V, false); // 既に見たことがある頂点か記録する
stack<int> st;
st.emplace(s); // sから探索する
seen[s] = true;
while (st.size() != 0) { // 深さ優先探索
int state = st.top(); // 現在の状態
st.pop();
for (auto next : G[state]) {
if (!seen[next]) { // 未探索の時のみ行う
seen[next] = true;
st.emplace(next); //次の状態をqueueへ格納
}
}
}
if (seen[t]) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
return 0;
}
隣接リスト・再帰関数を用いたC++での実装例は以下のようになります。
#include <bits/stdc++.h>
using namespace std;
using Graph = vector<vector<int>>;
// 深さ優先探索
vector<bool> seen; // 既に見たことがある頂点か記録
void dfs(const Graph &G, int v) {
seen[v] = true;
for (auto next : G[v]) {
if (!seen[next]) { // 訪問済みでなければ探索
dfs(G, next);
}
}
}
int main() {
int V, E;
cin >> V >> E;
int s, t;
cin >> s >> t;
Graph G(V);
for (int i = 0; i < E; i++) {
int a, b;
cin >> a >> b;
G[a].push_back({b});
// G[b].push_back({a});
}
seen.assign(V, false); // 初期化
dfs(G, s);
if (seen[t]) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
return 0;
}
問題2:DFSで同じ連結成分にあるか判定する(グリッドグラフ)
グリッドグラフ上でも、同じ連結成分にあるか判定することができます。AtCoder ATC001 A – 深さ優先探索 を解いてみましょう。
問題概要
スタート( s )・ゴール( g )・道( . )・壁( # )で構成されたH行W列のマスについて、スタートから壁を通らずにゴールまでたどりつけるか判定してください。
考え方
スタートから深さ優先探索をすると、ゴールに到達するか判定することができます。
グラフではなく、マス目でできた迷路上の探索なので、先程の例とプログラムの書き方が少し違いますが、基本的なアルゴリズムの考え方は変わりません。
隣り合うマス目を、再帰関数で探索してください。このとき、既に探索したことのあるマス目は探索しないようにしないと、無限ループに陥ってしまいます。
プログラム例
再帰関数での例を以下に示します。スタックを用いることでも同様に探索することができます。
#include <bits/stdc++.h>
using namespace std;
using P = pair<int, int>;
int H, W;
vector<vector<char>> maze; // 迷路の内容を保存する配列
vector<vector<bool>> seen; // 既に通った場所なのかを記録しておく配列
P s, g;
// dfs
int dx[4] = {1, -1, 0, 0}; // dx,dy は次の探索場所への距離を表す(4方向分)
int dy[4] = {0, 0, 1, -1};
void dfs(P p) {
seen[p.first][p.second] = true;
for (int i = 0; i < 4; i++) {
int ny = p.first + dy[i]; // 次の探索場所の行番号
int nx = p.second + dx[i]; // 次の探索場所の列番号
if (ny < 0 || H <= ny || nx < 0 || W <= nx) continue; // 迷路の外に出るならスルー
if (maze[ny][nx] == '#') continue; // 障害物があればスルー
if (seen[ny][nx]) continue; //探索済みならスルー
dfs(make_pair(ny, nx));
}
}
int main() {
cin >> H >> W;
maze.assign(H, vector<char>(W, '.'));
for (int i = 0; i < H; i++) {
for (int j = 0; j < W; j++) {
cin >> maze[i][j];
if (maze[i][j] == 's') {
s = make_pair(i, j);
} else if (maze[i][j] == 'g') {
g = make_pair(i, j);
};
}
}
seen.assign(H, vector<bool>(W, false));
dfs(s);
if (seen[g.first][g.second]) {
cout << "Yes" << endl;
} else {
cout << "No" << endl;
};
return 0;
}
練習問題
- AOJ ALDS1_11_B Depth First Search
- AtCoder ATC001 A – 深さ優先探索
- AOJ How Many Islands?:連結成分を数える問題です
- [AtCoder] ABC138 D – Ki :一工夫を加えて深さ優先探索を行いましょう
ディスカッション
コメント一覧
まだ、コメントがありません