木DPと全方位木DPを基礎から抽象化まで解説【競技プログラミング】

2020年4月3日動的計画法単位元,動的計画法,木,テーマ記事,競プロ,モノイド,結合則,木DP,部分木,全方位木DP

競技プログラミングでよく出題される木DPについての説明と、木DPで解ける一部の問題を同じ計算量で全頂点について求められるように応用した全方位木DPについて解説します。

木DP

基本的な考え方とイメージ

木DP とは、根を一つ固定した木について、以下のように部分木に関する値を利用して計算する動的計画法です。

dp[ v ] := 頂点 v を根とする部分木についての何かしらの値

木が N 頂点から構成されるなら、部分木も N 個できます。よって dp の値を N 個分計算することになります。

それぞれの部分木から、ボトムアップ的に dp を計算していきます。子を根とする部分木を組み合わせて新しい木をつくるイメージです。

以下は dp[ 1 ] を計算する際に、dp[ 2 ], dp[ 3 ], dp[ 4 ] を利用していることを表したイメージです。

頂点2・３・４を根とする部分木３つ

子を利用して頂点１を根とする（部分）木を構成

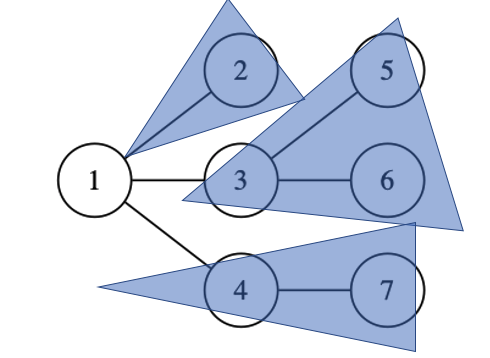
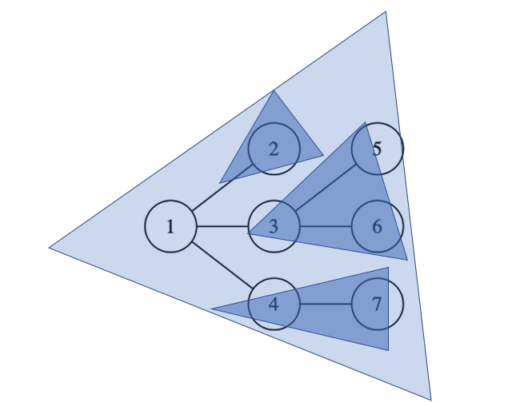
具体的な例題を通して、木DPの考え方を学んでから抽象化を行い、具体的な実装を見ていくことにします。

例題：根から最も遠い点までの距離を求める

木DPによって根 r から最も遠い点までの距離を求めることを考えてみましょう。この問題は木DPでなくても解くことが可能ですが、設定が単純かつ様々な問題に応用することができます。

木DPの基本は、部分木ごとに考えることです。以下のような動的計画法を考えてみましょう。

dp[ v ] := 頂点 v を根とする部分木について、v から最も遠い点までの距離

求めたい答えは、dp[ r ] の値です。

dp の漸化式を考えてみる

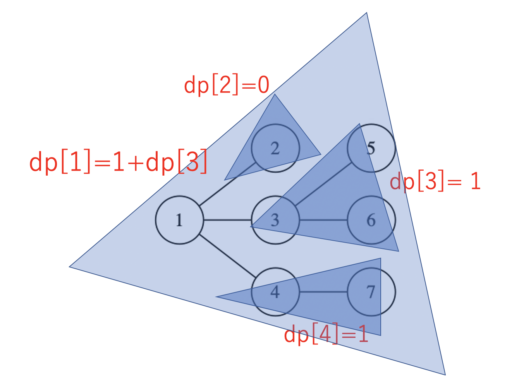
右の図のような例を考えてみましょう。

dp[ 1 ] の値を求めるのに、頂点 1 の子を根とする部分木に関する dp の値を利用することができます。

dp[ 1 ] の値の候補は

  • 1 + dp[ 2 ] = 1
  • 1 + dp[ 3 ] = 2
  • 1 + dp[ 4 ] = 2

となります。この中の最大となるものなので、「1+dp[3]」or「1+dp[4]」が採用され、dp[ 1 ] = 2 となります。

つまり、dp の更新式は以下のようになります。（ u は頂点 v の子、cost(v,u) は頂点 v, u 間の距離としています）

  • dp[ v ] = 1 + max(dp[ u ])

具体的な dp の計算方法：DFS の帰りがけ順

末端の部分木の値から計算していき、最終的に頂点 r を根とする木の値を計算したいです。

深さ優先探索で探索する頂点の順番は「行きがけ順」と「帰りがけ順」がありますが、「帰りがけ順」で上手く計算することができます。

計算量

DFSによって全ての部分木について dp の値を計算するので、基本的に計算量は頂点数を N として \(O(N)\) になります。

木DPの簡単な抽象化

max という関数のかわりに二項演算 \(•\) を用いて抽象化すると、以下のような手順で計算できることがわかります。

  1. 頂点 v の子 \(u_1, u_2, u_3, …, u_k\) について、 \(dp[u_1] • dp[u_2] • dp[u_3] • … • dp[u_k]\) を計算する（max(dp[u]) に対応）
  2. 先程計算した値を利用して、dp[ v ] を計算する（ max(dp[u]) に 1 を足すことに対応）

ほとんどの木DPは、問題ごとに計算内容の細かい違いはありますが、以上の2つの手順で計算することができます。

実装方法：根から最も遠い点までの距離を求める

以上の話をまとめて、例題の「根から最も遠い点までの距離を求める」木DPの実装をしてみましょう。

抽象化したときの、

  • 「1.」に対応する二項演算：merge
  • 「2.」に対応する演算：add_root

として DFS の帰りがけ順で計算すると以下のようになります。

function<int(int, int)> merge = [](int dp_cum, int d) -> int {  // 1.の二項演算を表す
    return max(dp_cum.dp, d.dp);
};
function<int(int)> add_root = [](DP d) -> int {  // 2.を表す。まとめたDPを用いて、新たな部分木のDPを計算する
    return DP(d.dp + 1);
};

void dfs(int v, int p = -1) {  // 頂点v, 親p
    int deg = G[v].size();     // 頂点vの次数
    if (deg == 1) {            // 末端にいる時
        dp[v] = 0;
        return;
    }
    int dp_cum = 0;
    for (int i = 0; i < deg; i++) {
        int u = G[v][i].to;          // u: vの子
        if (u == p) continue;        // 親なら探索しない
        dfs(u, v);                   // dp[u] の計算
        dp_cum = merge(dp_cum, dp[u]);  // 1.の二項演算
    }
    dp[v] = add_root(dp_cum);  // 2.の計算
}

細かい実装はわかりにくくなるので省いています。 dfs(r) を実行すれば、r を根とした木の r から最も遠い点への距離が求まります。

全方位木DP

木DPは「根を固定して（一つとして）」根に関する何らかの値をDPを利用して求めました（例：根から最も遠い点までの距離）。

これを、「それぞれの頂点を根として」すべての場合について根に関する何らかの値を求めたい時を考えます（例：全ての頂点について、それを根とした時の最も遠い点までの距離を求める）。

単純に木DPを全ての頂点について行うと、\(O(N)\) 程度の計算量を N 回行うことになるので、全体では \(O(N^2)\) となります。

しかし、全方位木DPと呼ばれる方法を用いると、木DPで解けた一部の問題を \(O(N)\) で計算できるようになります。

基本的な考え方とイメージ

基本は先程の木DPで、それを拡張したものが全方位木DPです。以下のようなDPを考えます。

dp[ v ][ i ] := 頂点 v を根とする部分木について、「v から出る i 番目の有向辺に対応する部分木」に関する何らかの値

普通の木DPは「頂点ごとに」部分木を対応させました。

しかし、全方位木DPは様々な頂点を根として考えるので、「有向辺ごとに」部分木を対応させると上手くいきます。

どんな頂点を根とした木の、どんな部分木であっても、これで一対一に対応させることができます。（ただし、例外として、元々の木に対応する有向辺は存在しないので注意です。）

頂点数が N とすれば、有向辺の数は 2(N-1) です。動的計画法を用いて上手く計算をすることができれば、\(O(N)\) で全ての部分木に関する dp の値を求めることができます。

有向辺ごとに部分木を対応させる

dp の計算方法

全体の計算の概要は以下のようになります。

  1. DFS: ある一つの頂点 v を根として、普通の木DPを行う
  2. BFS: v から頂点を一つずつズラしていき、必要な dp の計算を行う

それぞれ詳しく見ていきます。

ステップ1: DFSで普通に木DPを行う

深さ優先探索を用いて、通常の木DPと同様の計算を行います。

dp の配列の形が多少異なるだけで、木DPとの違いはほぼありません。

これで求まる有向辺（と部分木）は右図のようになります。

頂点 1 を根として木DPを行った時に求まる部分木

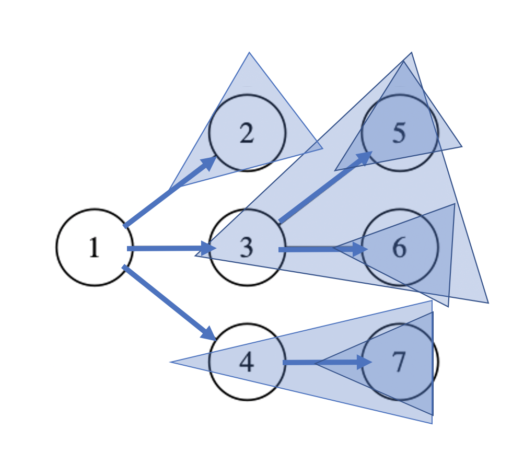
ステップ2: BFSで必要なdpの計算を行っていく

先程もとめた頂点から、少しずつ必要な dp の値を求めていきます。

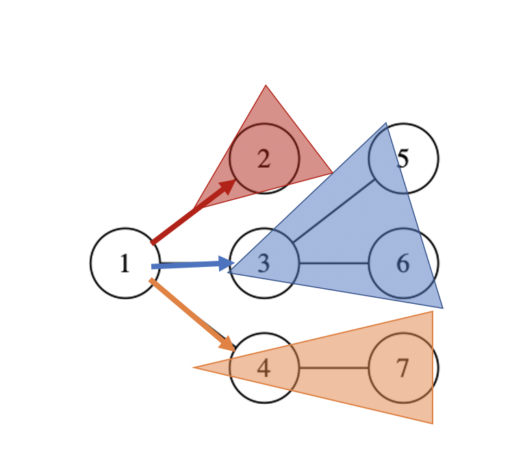
例えば左図のように、4→1 の有向辺に対応する赤い部分木を求めることを考えます。

これは、既に求めた部分木を組み合わせて求めることが可能です。

赤：求めたい部分木、青：赤を求めるのに必要な部分木

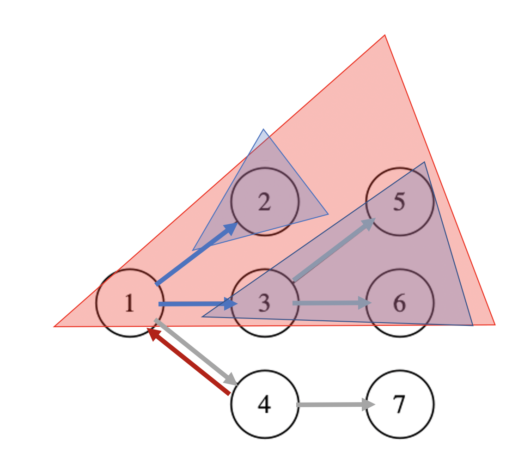
頂点1 に関して言えば、以下のように3通り考えることができます。

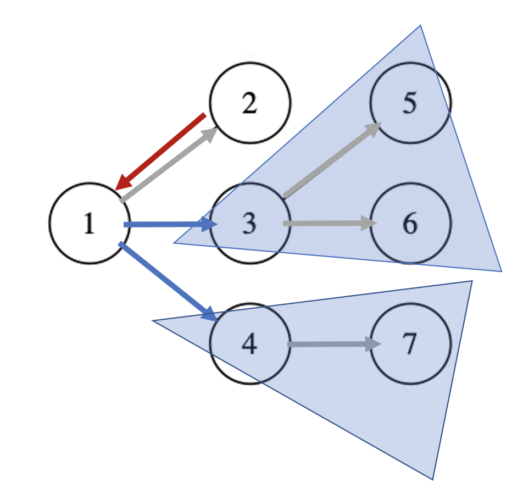
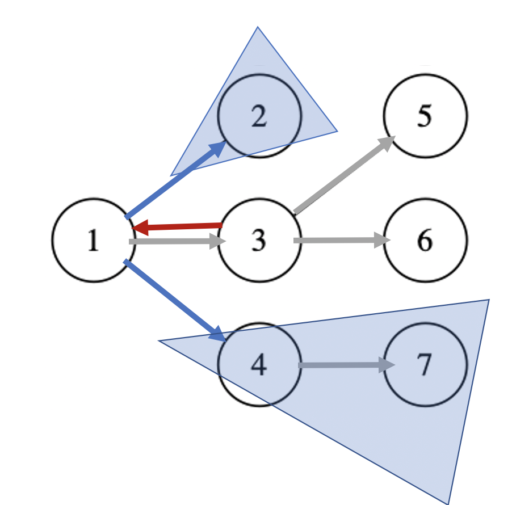
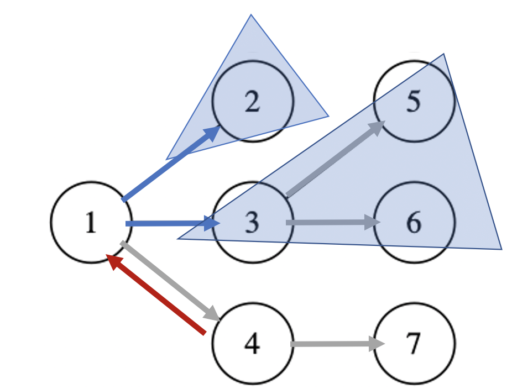
次数が 3 の頂点 1 については、頂点 1 に入る有向辺（上図の赤い辺）に対応する部分木に対応する dp を求めるのに必要な（青い）部分木の数は、「(次数3) – 1 = 2」となるので、全体では 3*2 だけ計算が必要です。

もう少し一般的にすると、次数が d の頂点 v について、v に入る赤い有向辺の計算には、d*(d-1) だけ計算が必要となってしまいます。つまり一つの頂点あたりに \(O(d^2)\) 必要です。

しかし、これは「累積和」的な考え方を利用すると、\(O(d)\) まで減らすことができます。

以下のように、左右からの「累積 merge」を考えると、一つの部分木を求めるのに \(O(1)\) で済むためです。

左からの累積merge
右からの累積merge
\(O(1)\) で必要なmergeができる

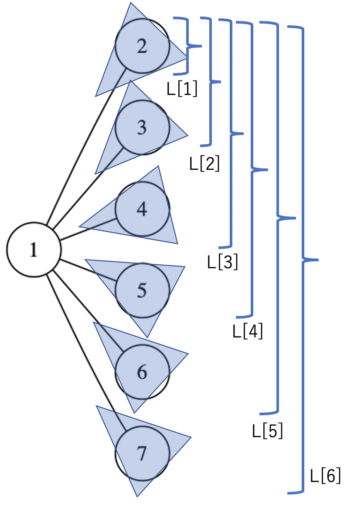
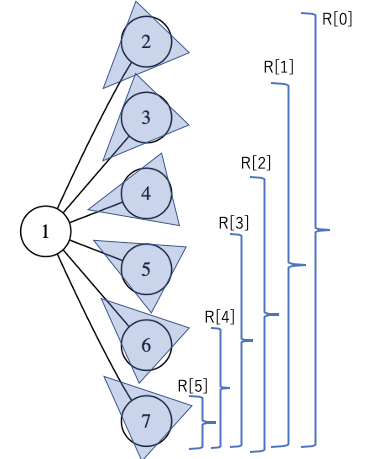
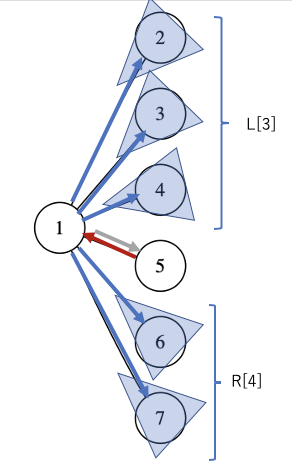
以上より、「頂点ごとの次数の和」が最終的な計算量になります。これは、辺の数の２倍に等しいので、全体では \(O(N)\) で計算ができました。

どのような状況で全方位木DPが使えるか

部分木の dp の値を merge する関数ですが、「モノイド」を利用して抽象化できることが知られています。

モノイドとは、集合 X と 、X 上の二項演算 \(•\): X × X → X について

  • 結合則：X の任意の元 \(a,b,c\) について、\(a•(b•c) = (a•b)•c\)
  • 単位元 e の存在：Mの任意の元 a について、\(e•a = a•e = a\) を満たす X の元 e が存在する

が同時に成り立つようなものを言います。

今回で言えば、二項演算 \(•\) というのは、merge のことです。「累積 merge」を行うための条件として「モノイドであること」が必要となるのです。

実装例

「全ての頂点について、それを根とした時の最も遠い点までの距離」を全方位木DPで求めるときの実装例です。

他の問題に応用しやすいように、dp の値を構造体としたり、merge 関数・add_root 関数を定義したりしています。

#include <bits/stdc++.h>
using namespace std;

/* Rerooting: 全方位木 DP
    問題ごとに以下を書き換える
    - 型DPと単位元
    - 型DPに対する二項演算 merge
    - まとめたDPを用いて新たな部分木のDPを計算する add_root
    計算量: O(N)
*/
struct Rerooting {
    /* start 問題ごとに書き換え */
    struct DP {  // DP の型
        long long dp;
        DP(long long dp_) : dp(dp_) {}
    };
    const DP identity = DP(-1);  // 単位元(末端の値は add_root(identity) になるので注意)
    function<DP(DP, DP)> merge = [](DP dp_cum, DP d) -> DP {
        return DP(max(dp_cum.dp, d.dp));
    };
    function<DP(DP)> add_root = [](DP d) -> DP {
        return DP(d.dp + 1);
    };
    /* end 問題ごとに書き換え */

    // グラフの定義
    struct Edge {
        int to;
    };
    using Graph = vector<vector<Edge>>;

    vector<vector<DP>> dp;  // dp[v][i]: vから出るi番目の有向辺に対応する部分木のDP
    vector<DP> ans;         // ans[v]: 頂点vを根とする木の答え
    Graph G;

    Rerooting(int N) : G(N) {
        dp.resize(N);
        ans.assign(N, identity);
    }

    void add_edge(int a, int b) {
        G[a].push_back({b});
    }
    void build() {
        dfs(0);            // 普通に木DP
        bfs(0, identity);  // 残りの部分木に対応するDPを計算
    }

    DP dfs(int v, int p = -1) {  // 頂点v, 親p
        DP dp_cum = identity;
        int deg = G[v].size();
        dp[v] = vector<DP>(deg, identity);
        for (int i = 0; i < deg; i++) {
            int u = G[v][i].to;
            if (u == p) continue;
            dp[v][i] = dfs(u, v);
            dp_cum = merge(dp_cum, dp[v][i]);
        }
        return add_root(dp_cum);
    }
    void bfs(int v, const DP& dp_p, int p = -1) {  // bfs だが、実装が楽なので中身は dfs になっている
        int deg = G[v].size();
        for (int i = 0; i < deg; i++) {  // 前のbfsで計算した有向辺に対応する部分木のDPを保存
            if (G[v][i].to == p) dp[v][i] = dp_p;
        }
        vector<DP> dp_l(deg + 1, identity), dp_r(deg + 1, identity);  // 累積merge
        for (int i = 0; i < deg; i++) {
            dp_l[i + 1] = merge(dp_l[i], dp[v][i]);
        }
        for (int i = deg - 1; i >= 0; i--) {
            dp_r[i] = merge(dp_r[i + 1], dp[v][i]);
        }

        ans[v] = add_root(dp_l[deg]);  // 頂点 v の答え

        for (int i = 0; i < deg; i++) {  // 一つ隣の頂点に対しても同様に計算
            int u = G[v][i].to;
            if (u == p) continue;
            bfs(u, add_root(merge(dp_l[i], dp_r[i + 1])), v);
        }
    }
};

int main() {
    int N;
    cin >> N;
    Rerooting reroot(N);
    for (int i = 0; i < N - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        reroot.add_edge(u, v);
        reroot.add_edge(v, u);
    }
    reroot.build();

    for (int i = 0; i < N; i++) {
        cout << "頂点" << i + 1 << ": " << reroot.ans[i].dp << endl;
    }
}

入力例：

6
1 2
1 3
3 4
3 5
5 6

出力例：

頂点1: 3
頂点2: 4
頂点3: 2
頂点4: 3
頂点5: 3
頂点6: 4

練習問題

木DP

全方位木DP

動的計画法単位元,動的計画法,木,テーマ記事,競プロ,モノイド,結合則,木DP,部分木,全方位木DP