ビット全探索（ 2^n 通りの全探索）

2019年11月22日探索再帰関数,bit演算

ビット全探索とは

bit演算を上手く用いると、それぞれの要素に対して「使うか」「使わないか」の2通りがあるような、\(2^n\) 通りの場合を全探索することができます。

言い換えると、集合 \(\{0,1,2,3,…,n-1\}\) の部分集合を全て調べ上げることができます。

（ループ文を用いた全探索では、２重ループのときは \(n^2\) 通りの場合、3重ループのときは \(n^3\) 通りの場合を全て調べましたが、これでは指数通りの全探索は行うことができません。）

ループ文を用いた全探索に比べると計算時間が爆発的に増えてしまうので、あまり大きな入力に対して行うとかなりの時間がかかってしまいます。余裕があれば実際にためして見ると良いでしょう。
(参考:計算量同士の比較と入力サイズによる比較)

具体例

\( \{4, 10, 1\}\) という3個の数字が与えられた時の選び方は、\(\{\},\{4\}, \{10\},\{1\}, \{4,10\},\{4,1\},\{10,1\},\{4,10,1\}\) の \(2^3=8\) 通りです。

ビット全探索は、この \(2^3=8\) 通りを全て調べ上げるような探索方法です。

bit演算を用いたアルゴリズム

bit演算とループを用いることで \(2^N\) 通りの場合をすべて確かめることができます。

２進数で要素を選択するイメージ

例えば、\( \{4, 10, 1\}\) をビット全探索する場合を考えてみましょう。

これの部分集合である \( \{4,\_ , 1\}\) を 2 進数(bit)で表した \(101_2\) に対応させて考えてみます。

\(i\) 桁目が 1 なら「\(i\)番目を選ぶ」, 0 なら「\(i\)番目を選ばない」に対応させます。この場合では、\( \{4, 10, 1\}\) のうち\( 4, 1\) を選んだことになります。

\(5\) を2進数(bit)で表すと\(101\)になります。

アルゴリズム

  1. \(b=0\) とする
  2. \(b\) の値から、ビットが立っている場所を確認する。ビットと対応する場合について、探索の条件を満たすか判定する
  3. \(b\) が \(2^n\) 以上なら終了。そうでないなら、1増やして2に戻る

ビットが立っている場所を確認するのに、ANDやORなどのビット演算に関する知識が必要です。慣れないうちは難しいかもしれません。

再帰関数を使ったアルゴリズム

再帰関数を用いた場合は、ビット全探索と呼ぶことはほぼ無いですが、こちらでも \(2^N\) 通りの探索を行うことができるので紹介します。

再帰関数というのは、「自身を呼び出す関数」のことです。この再帰関数を使って「選ぶ」「選ばない」を決定し、それぞれで自身を分岐させて呼び出します。

つまり、関数内で、「選ぶ」と決めた時の再帰関数と、「選ばない」と決めた時の再帰関数を、それぞれ呼び出せばよいのです。

イメージとしては下の図のように、分岐させるたびに「選ぶ」・「選ばない」を決定させていくような形です。（下の図では1で「選ぶ」、0で「選ばない」を表しています。）

再帰関数による分岐の様子

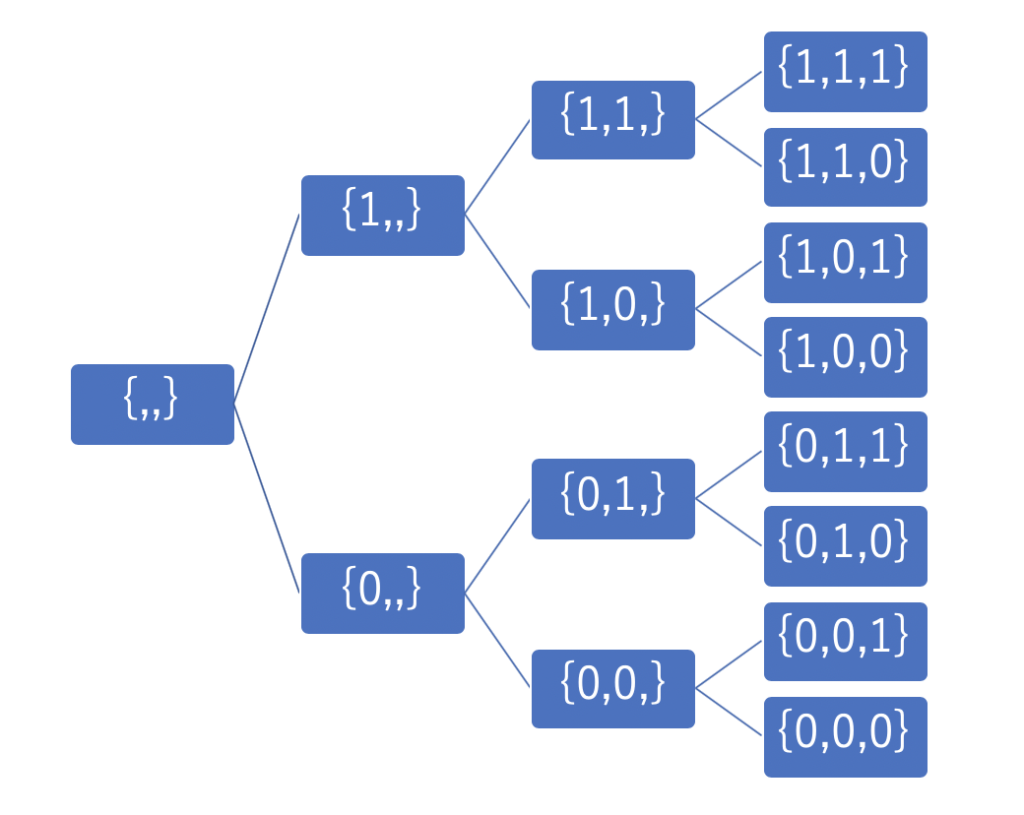
次に説明するbit演算を用いたアルゴリズムは、\(2^n\)通りの状態しか列挙できませんが、再帰関数の呼出しを増やせば、\(3^n\)通りや\(5^n\)通りの全探索も行うことができます。

実はこれは深さ優先探索でもあります。

問題例: すべての場合の和を計算する

使い所がわかりにくいので具体例を使って考えてみましょう。

問題

値が違う \(n\) 個の数字が与えられます。選び方をすべての場合について考えたとき、それぞれの場合で選んだ数値の和を、さらにすべて足して和を求めて下さい。

入力と出力の例

\( \{4, 10, 1\}\)という3個の数字が与えられた時を考えます。

このときの選び方は、\(\{\},\{4\}, \{10\},\{1\}, \{4,10\},\{4,1\},\{10,1\},\{4,10,1\}\)の\(2^3=8\)通りです。

それぞれの場合での選んだ数値の和は、\(0,4,10, 1, 14,5,11,15\)となります。

さらに全ての場合を足すと、60となるので、答えは60です。

プログラム例(bit演算)

C++の例

#include <bits/stdc++.h>
using namespace std;

int main() {
    vector<int> list = {4, 10, 1};
    int ans = 0;
    for (int bits = 1; bits < (1 << (int)list.size()); bits++) {  // 2^3 の全ての場合を探索する
        int sum = 0;
        for (int i = 0; i < (int)list.size(); i++) {
            int mask = 1 << i;
            if (bits & mask) {  // i番目のbitが立っていれば加算する
                sum += list[i];
            }
        }
        ans += sum;
    }
    cout << ans << endl;
}

Pythonの例

list = [4,10,1]
def bit_plus(list):
  sum = 0
  for bit in range(1<<len(list)): # 0(0b000)から7(0b111)まで
    for i in range(len(list)):
      mask = 1 << i
      if bit&mask: # 右からi番目にビットが立っているかどうか判定
        sum += list[i]
  return sum

print(bit_plus(list)) # 出力は60

プログラム例(再帰関数)

Pythonの例(Colaboratory などで確認してみて下さい）

list = [4,10,1]

def rec_plus(list, now ,sum): # sum は現在までの和を保持するために用いる
  if now<3:
    # now番目を足す時 + now番目を足さない時
    return rec_plus(list, now+1, sum+list[now]) + rec_plus(list, now+1, sum) 
  else:
    return sum
  
print(rec_plus(list,0,0)) # 出力は60

練習問題

  • [AtCoder] ABC128 C – Switches：基本的なビット全探索です。スイッチのオンオフをビットで表現しましょう
  • [AtCoder] ABC147 C – HonestOrUnkind2：「正直か」「不親切か」をビットで表現して全探索すれば良いです。矛盾がない状況で正直者は最大何人かを出力しましょう

探索再帰関数,bit演算