プリム法による最小全域木を求めるアルゴリズム
無向グラフ \(G=(V,E)\) について、\(G\) の部分グラフ \(T\) が以下を満たす時、\(T\) は全域木(Spanning Tree) と言います。
- \(T\) は木
- \(T\) では\(V\) の任意の2頂点を連結にする(\(T\) は \(G\) の頂点 \(V\) を全て使っている)
特に \(T\) で使われる辺のコストの和が最小であるときは、最小全域木(MST: Minimum Spanning Tree)と呼ばれます。

プリム法は、最小全域木(とその辺のコストの総和)を求めるアルゴリズムです。同様に最小全域木を求めるアルゴリズムとしてクラスカル法があります。
アルゴリズム
プリム法:
- はじめに、適当に選んだ頂点 1 つのみを \(T\) に含めると確定させる
- 以下をすべての頂点が \(T\) に含まれるまで繰り返す
- 全ての「既に確定した頂点」から「まだ確定していない(\(T\) に含まれていない)頂点 」へ伸びる辺を全て確認して、最小のコストの辺 e=(u,v) を選ぶ。そして v を \(T\) に含めることにする。
※ アルゴリズムとしては、ダイクストラ法に似ています。
計算量
- ヒープを使わない場合:
- \(O(|V|^2)\)
- ヒープを使う時:
- \(O(|E| \log |V|)\)
ダイクストラ法と同様に、毎回全ての頂点を確認して最小のコストの辺を探すと \(O(|V|)\) だけかかります。それを頂点数だけ繰り返すことになるので、全体としては \(O(|V|^2)\) です。
しかし、ヒープなどのデータ構造を利用することにより、候補の挿入や削除を \(O(\log |V|)\) で行うことができます。これを全ての辺に対して行うことになるので全体では \(O(|E| \log |V|)\) です。
C++ での実装例
ヒープを使わない \(O(|V|^2)\) のアルゴリズムで、AOJ ALDS1_12_A Minimum Spanning Tree を解く実装例です。グラフ \(G\) を与えられて、最小全域木の辺の重みの総和を求めます。
ヒープを使わない場合は、隣接行列で表現されたグラフに対して実装しやすいという特徴があります。
隣接リストを使う場合はクラスカル法などのアルゴリズムで \(O(|E| \log |V|)\) で実装できるので、状況によって使い分けると良いでしょう。
#include <bits/stdc++.h>
using namespace std;
vector<vector<int>> G; // 隣接行列での表現
/* Prim : プリム法で minimum spanning tree を求める構造体
入力: 隣接行列でのグラフ G
最小全域木の重みの総和: sum
計算量: O(|V|^2)
*/
struct Prim {
const int INF = 1e9;
int sum; // MSTの重みの総和
int n; // 頂点数
vector<int> mincost; // 既に確定した頂点からの最小コスト(確定済みから行けない時は INF)
vector<bool> used; // 既に確定したかどうか
Prim(vector<vector<int>> const& Graph) {
init(Graph);
}
void init(vector<vector<int>> const& Graph) {
n = (int)Graph.size();
mincost.assign(n, INF);
used.assign(n, false);
sum = 0;
mincost[0] = 0; // 始め頂点0からスタートさせる
while (true) {
int v = -1;
for (int u = 0; u < n; u++) { // コストが最小で行ける頂点 v を探す
if (!used[u] && (v == -1 || mincost[u] < mincost[v])) v = u;
}
if (v == -1) break; // MST ができたので終了
used[v] = true;
sum += mincost[v];
for (int u = 0; u < n; u++) { // 確定した頂点から行ける頂点について、最小コストを更新
if (Graph[v][u] != -1) mincost[u] = min(mincost[u], Graph[v][u]);
}
}
}
};
int main() {
int n;
cin >> n;
G.assign(n, vector<int>(n));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> G[i][j];
}
}
Prim prim(G);
cout << prim.sum << endl;
return 0;
}
プリム法の気持ち
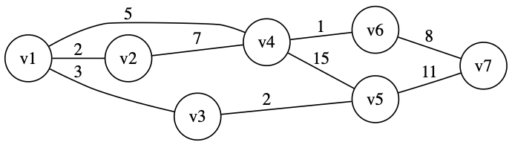
以下のグラフ \(G\) の最小全域木をプリム法で求めてみます。

・まずは適当に選んだ v1 を確定させる
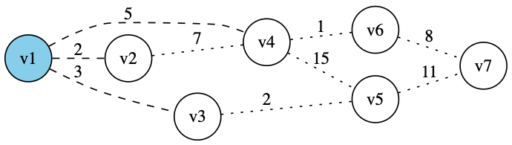
・確定済みと未確定の頂点に接続する辺の中で、コストが最小なのは辺 (v1,v2) なので、 v2 を確定させる
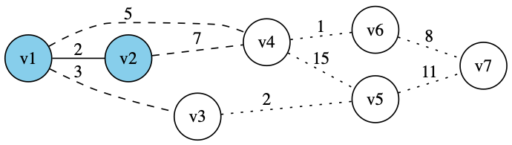
・確定済みと未確定の頂点に接続する辺の中で、コストが最小なのは辺 (v1,v3) なので、v3 を確定させる

・確定済みと未確定の頂点に接続する辺の中で、コストが最小なのは辺 (v3,v5) なので、v5 を確定させる
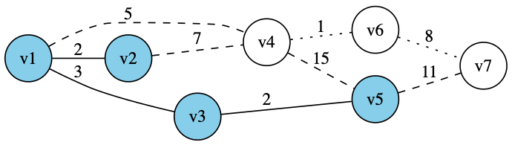
・確定済みと未確定の頂点に接続する辺の中で、コストが最小なのは辺 (v1,v4) なので、v4 を確定させる
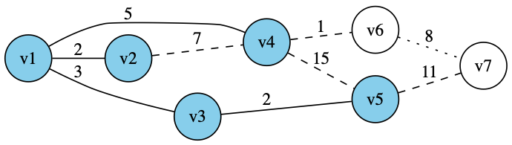
・確定済みと未確定の頂点に接続する辺の中で、コストが最小なのは辺 (v4,v6) なので、v6 を確定させる

・確定済みと未確定の頂点に接続する辺の中で、コストが最小なのは辺 (v6,v7) なので、v7を確定させる(辺 (v2,v4) の方がコストが小さいが、どちらも確定済みの頂点)
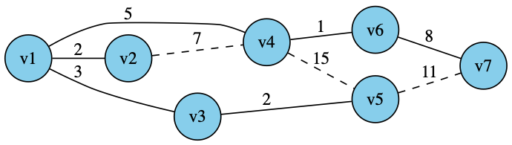
以上より最小全域木が求まりました。
ディスカッション
コメント一覧
まだ、コメントがありません