二分探索(Binary Search)のアルゴリズム

2019年11月22日探索基本,二分探索

初級編：二分探索とは

二分探索とは、ソート済みである配列の中から、目的の値が存在するかを調べる探索アルゴリズムです。高速でわかりやすいため非常に良く使われます。

線形探索はソートしていない配列でも探索することができます。二分探索は、配列がソート済みであるという条件があるものの、線形探索よりも高速に探索することができます。

２分探索の計算量は\(O(logn)\)なので、線形探索の計算量\(O(n)\)に比べて非常に高速です。

二分探索の気持ち

大きさが順番になるように並べられた数列 {3,8,14,31,55,72,98} の中から、72 をどのように二分探索するのかを見ていきましょう。

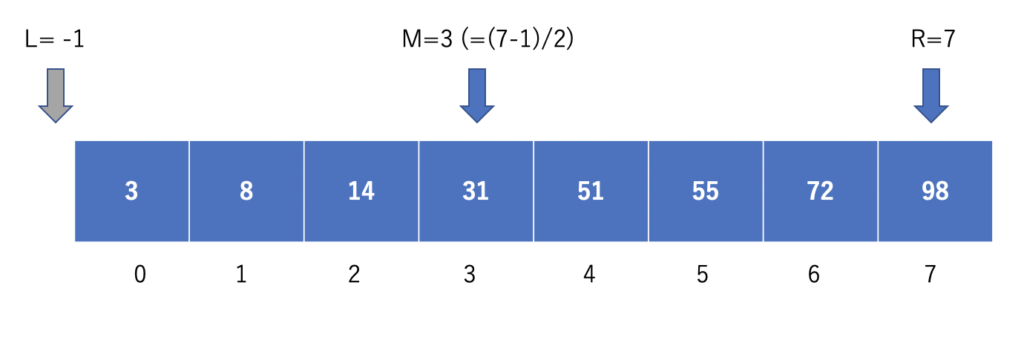
二分探索では上図のように、探索範囲の左端(L)と中心(M)と右端(R)に注目します。中心であるMが指す値が 31 なので、72はこれより右側にあるはずです。よって、探索範囲は以下のように半分に減らせます。

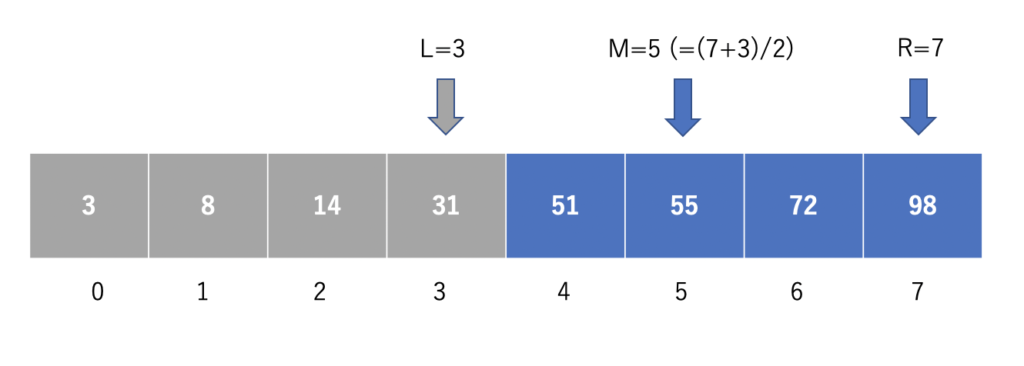
同様に、Mが指す値は55なので、72はこれよりも右側にあるはずです。

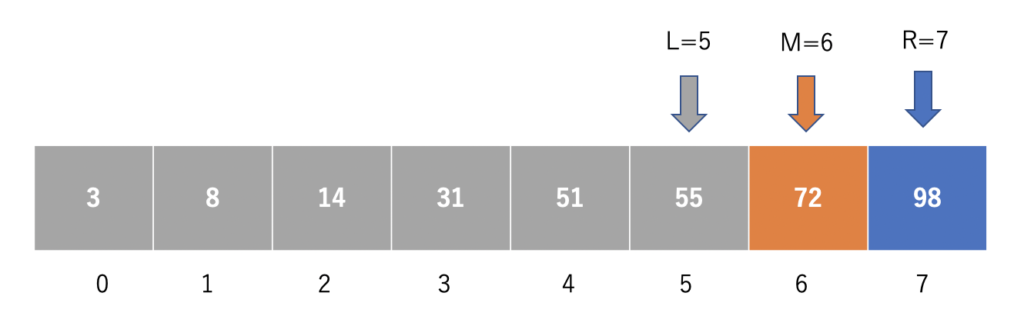
これで72を発見することができました。

ソート済み配列からxを探索するアルゴリズム

二分探索の基本は「ソート済み配列内のどこにxが存在するか」を調べる時に用いられます。配列は昇順(小さいものが先頭)にソートされているものとします。

  1. L=-1, R=配列のindexの最大値 として以下を繰り返す
    1. R-L>1 でなければ x が存在しないか R が指す部分が x 。R-L>1なら以下を実行する
    2. LとRの中間にあるMが指す要素について、xとの大小関係を調べる
      1. xと等しければ、Mが指すindexを出力して終了する
      2. xの方が大きければ、右側半分にある部分配列に対して1と2の探索を行う（LをMがあった場所に移す）
      3. xの方が小さければ、左側半分にある部分配列に対して1と2の探索を行う（RをMがあった場所に移す）

以下のことに注意するとより分かりやすいと思います。

  • Lから左側 と Rより右側：x が絶対に存在しない範囲
  • Lより右側~Rまで：x が存在する可能性がある範囲

存在する可能性のある範囲を、段々と半分に分けて（二分して）絞っていくイメージです。

計算量

配列の長さがnだとすると、一度中間を調べるごとに調べるべき配列が半分になるので、平均と最悪の計算量は \(O(logn)\) になります。

はじめに目的の値が見つかるときを考えると、最善の計算量は \(O(1)\) になります。

計算量の証明について（上級者向け）

配列の長さをn、またcを定数として、二分探索の計算量は、

$$T(n) = T(n/2) + c$$

で表すことができます。ここから、マスター定理やRecursion Tree Method などを用いることで先程の計算量を見積もることができます。

プログラム例

数列 arr = [1,4,5,8,10,24,55,66,190] の中から指定された数がどこにあるか二分探索するプログラムです。存在しない場合は -1 を返します。

Pythonでの例 (Colaboratory などで確認してみて下さい）

def binary_search(arr,x): 
  #l,rはどこからどこまでの配列を調べるかを与えます
  l = -1
  r = len(arr) - 1
  while r-l>1:
    mid = l + (r-l)//2
    if x == arr[mid]:  # xがちょうど中間にあったとき
      return mid
    elif x < arr[mid]: # xが左側の配列にあるとき
      r = mid
    else:              # xが右側の配列にあるとき
      l = mid
  if x==arr[r]:
      return r
  return -1


arr = [1,4,5,8,10,24,55,66,190]
print(binary_search(arr,55))   # 出力は6
print(binary_search(arr,4))    # 出力は1
print(binary_search(arr,1000)) # 出力は-1

C++での例

#include <bits/stdc++.h>
using namespace std;
int binary_search(int arr[], int arr_len, int x) {
    int l = -1;
    int r = arr_len - 1;
    while (r - l > 1) {
        int mid = l + (r - l) / 2;
        if (x == arr[mid]) {
            return mid;
        } else if (x < arr[mid]) {
            r = mid;
        } else {
            l = mid;
        }
    }
    if (x == arr[r]) return r;
    return -1;
}

int main() {
    int arr[] = {1, 4, 5, 8, 10, 24, 55, 66, 190};
    int arr_len = sizeof(arr) / sizeof(arr[0]);
    cout << binary_search(arr, arr_len, 55) << endl; // 出力は6
    cout << binary_search(arr, arr_len, 4) << endl;　　// 出力は1
    cout << binary_search(arr, arr_len, 1000) << endl;  // 出力は-1
    return 0;
}

中級編：二分探索を使えるようになる

二分探索が用いられるのは「ソート済み配列内のどこにxが存在するか」を探索するだけではありません。

  • ソート済み配列内で x 以上(以降)の値を持つもののうち、左端にあるものは何か(最小のindexは何か？)
  • ソート済み配列内で x 以下(未満)の値を持つもののうち、右端にあるものは何か(最大のindexは何か？)

なども探索することができます。

競技プログラミングなどでは、むしろこちらの方がよく使われます。

x以上の値を持つもので左端のものを求めるアルゴリズム

先程の二分探索のアルゴリズムを若干変更するだけです。

  1. L=-1, R=配列のindexの最大値 として以下を繰り返す
    1. R-L>1なら以下を実行する
    2. LとRの中間にあるMが指す要素について、xとの大小関係を調べる
      1. x未満ならば、右側半分にある部分配列に対して1と2の探索を行う（LをMがあった場所に移す）
      2. x以上ならば、左側半分にある部分配列に対して1と2の探索を行う（RをMがあった場所に移す）
  2. Rが指す値が答え

C++での実装例

C++ では、標準で 「x 以上(以降)の値を持つもののうち、左端にあるもののindex」 を求める lower_bound 関数 とupper_bound 関数がサポートされています。

ここでは lower_bound などに関しては詳しく述べませんが、自分で実装する場合も用意された関数を使う場合も、どちらもできるようにしておくと良いでしょう。

#include <bits/stdc++.h>
using namespace std;
int my_lower_bound(const vector<int> &arr, int x) { // 自作のlower_bound: x以上の値を持つ左端のindexを返す
    int l = -1;
    int r = arr.size() - 1;
    while (r - l > 1) {
        int mid = l + (r - l) / 2;
        if (x == arr[mid]) {
            return mid;
        } else if (x < arr[mid]) {
            r = mid;
        } else {
            l = mid;
        }
    }
    return r;
}

int main() {
    vector<int> arr = {1, 4, 5, 8, 10, 24, 55, 66, 190};
    cout << my_lower_bound(arr, 6) << endl;
    cout << lower_bound(arr.begin(), arr.end(), 6) - arr.begin() << endl;
    cout << my_lower_bound(arr, 11) << endl;
    cout << lower_bound(arr.begin(), arr.end(), 11) - arr.begin() << endl;
    cout << my_lower_bound(arr, 55) << endl;
    cout << lower_bound(arr.begin(), arr.end(), 55) - arr.begin() << endl;

    return 0;
}

上級編：二分探索の一般化

さらに応用できるように、今までの二分探索をもう少し一般化してみると、

  • 条件 C(index) を満たすような最小の index を求めよ（左端）
  • 条件 C(index) を満たすような最大の index を求めよ（右端）

というような問題を二分探索で解くことができます。

条件には単調性が必要

二分探索が使えるような、条件 C(index) には「単調性」が求められます。

  • ある値で条件 C を満たしたならば、それ以降の値では必ず C を満たす
  • ある値で条件 C を満たさなければ、それ以降の値では必ず C を満たさない

などのどちらかが成り立っていれば良いです。

具体例

さきほどの lower_bound 関数で言えば、ソート済み配列 A において

  • C(index)： A[index] の値が x 以上

という条件を満たす最小の index を求めたのでした。

この条件 C にも単調性があります。それは「 A がソート済みである」という条件が生きてきて、

  • A[index] の値が x 以上だったら、A[index+1], A[index+2], A[index+3], … は全て x 以上

が成立するので単調です。

問題例：平均値の最大化

平均値の最大化や、最小値の最大化などを求めたい時に、２分探索が使えることがあります。

平均値の最大化の例として [AtCoder] ABC 034 D – 食塩水 を解いてみましょう。

問題概要

N 個の食塩水が与えられる。\(i\) 個目の食塩水は\(w_i\) の重さで濃度が \(p_i\) パーセントである。K 個の食塩水を混ぜた時の濃度として考えられる、最大の濃度を求めよ。

制約

  • \(1 \leq K, N \leq 1000\)
  • \(1 \leq w_i \leq 10^9\)
  • \(0 \leq p_i \leq 100\)

考え方

K個の食塩水を混ぜると濃度が平均化され、この値を最大化することを考えます。このように「平均の最大化」などは二分探索で求めることが良くあります。

二分探索のために、以下のような条件を考えましょう。

  • C(x)： 最終的にできた濃度の値が x 以上になる

この条件には以下のような単調性があるので、二分探索をすることができます。

  • ある値で C を満たしたら、それ以下の値 x でも必ず成立する

それでは、最終的な値 x を決め打ちしたときに、C が成り立つかを判定する方法を考える必要があります。

答えとなる K 個の食塩水の集合を \(K\) として、 x がどのような式を満たすか考えると以下が成立します。

\begin{align}
&\frac{\sum_{i \in K} w_i p_i/100}{\sum_{i \in K} w_i} \geq \frac{x}{100} \\
&\Leftrightarrow \sum_{i \in K} \frac{w_i p_i}{100} \geq \sum_{i \in K} \frac{w_i x}{100} \\
&\Leftrightarrow \sum_{i \in K} \frac{w_i p_i}{100} – \sum_{i \in K} \frac{w_i x}{100} \geq 0 \\
&\Leftrightarrow \sum_{i \in K} \frac{w_i p_i – w_i x}{100} \geq 0
\end{align}

この式が成り立つかどうかの判定は、\(\frac{w_i p_i – w_i x}{100}\) の値で降順にソートして K 個取った値が 0 以上かどうかを判定すれば良いです。

これは \(O(N \log N)\) で行うことができます。

解法

二分探索は小数にも使用することができます。

  1. ok=0.0, ng=101.0 として、ok と ng の間隔が十分小さくなるまで以下を繰り返す
    1. okとngの中間にある値 x について、以下の方法でC(x) が成立するか判定する
      1. \(\frac{w_i p_i – w_i x}{100}\) の値で降順にソートする
      2. 上位K個の合計が 0 以上ならC(x)成立。そうでないなら不成立となる
    2. C(x) が成立したならば、ok = mid と更新する。不成立ならば ng = mid と更新する
  2. ok の値が答え

C++ での実装例

判定時ですが、\(\frac{w_i p_i – w_i x}{100}\) は100で割らなくても正しく判定することができます。

#include <bits/stdc++.h>
using namespace std;

int N, K;
string S;
vector<double> w, p;

bool C(double x) {  // 条件を満たすか判定
    vector<double> A(N);
    for (int i = 0; i < N; i++) {
        A[i] = w[i] * (p[i] - x) / 100.0;
    }
    sort(A.begin(), A.end(), greater<double>());  // 降順にソート
    double sum = accumulate(A.begin(), A.begin() + K, 0.0);
    return (sum >= 0);
}

int main() {
    cin >> N >> K;
    w.resize(N);
    p.resize(N);
    for (int i = 0; i < N; i++) {
        cin >> w.at(i) >> p.at(i);
    }

    // 二分探索
    double ng = 100;
    double ok = 0.0;
    while (ng - ok > 1e-10) {  // [ok, ng) の範囲を探索する。二分探索で探索範囲を半分ずつにしていく
        double mid = (ok + ng) / 2.0;
        if (C(mid)) {
            ok = mid;
        } else {
            ng = mid;
        }
    }

    cout << setprecision(10) << ok << endl;

    return 0;
}

練習問題

基本

応用

最小・最大化問題に対して、条件を満たすかの判定が比較的簡単に行えれば、二分探索が上手くいく可能性があります。

単調性があれば二分探索を疑ってみましょう。

探索基本,二分探索