最悪・最善・平均時のアルゴリズムの計算量の見積もり
計算量は3つの場合を考える
「漸近記法」により数式の大体の大きさを見積もる方法を学びました。
しかし、アルゴリズムの計算量というものは、毎回常に同じ数式になるわけではありません。入力の大きさが同じであっても、形が違うだけで計算量と言うものは変化していきます。
そこで、アルゴリズムの計算量を考える際には
- 最悪の時(worst case)
- 最善の時(best case)
- 平均の時(average case)
の3つを評価する必要があるのです。
線形探索での具体例
基本的なアルゴリズムの1つ、「線形探索」を例に説明していきます。
線形探索とは、目的の物が、サイズが \(N\) のあるリストや配列に入っているかどうかを前から判定していくアルゴリズムのことです。
例えば、以下の図のような配列に、0が含まれているかを確認するときを考えてみます。
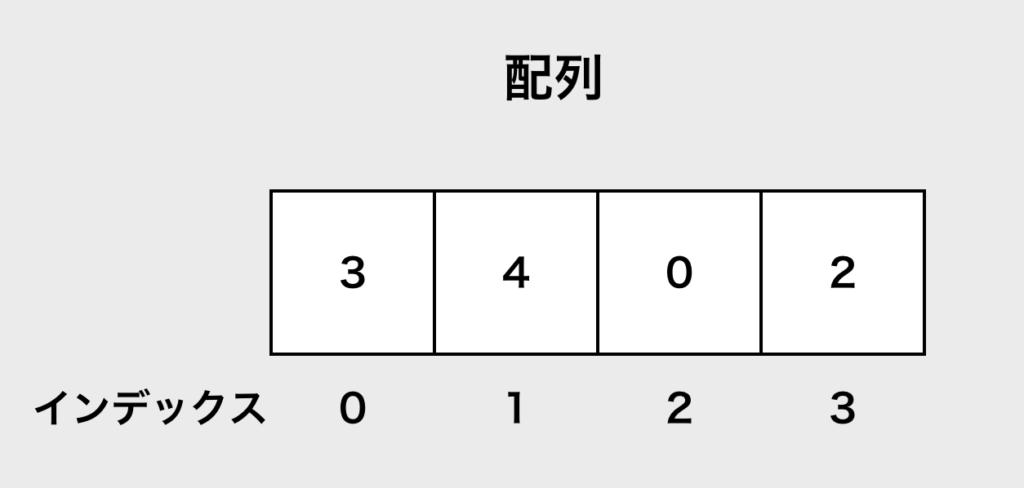
線形探索では前から見ていくので、 3→4→0 と見ていき 0 を発見した時点で終了します。今回では 3 回判定しました。
人間にとっては一目瞭然ですが、配列の長さが何万・何億と増えた場合は人間よりもコンピュータの方が有利でしょう。
最悪の時(worst case)
計算量を考えるときは最悪の場合を考えることが多いです。つまり、計算量の上限(上界)を考えることになります。
最大でどれだけの時間がかかるかを知っておかないと、いつ頃計算が終了するのかを想定することができません。場合によっては100年経っても終わらない可能性もあります。
線形探索の例を考えてみましょう。最悪の場合になるのは、配列内に目的の数が存在しない場合です。途中で終了することがないので、配列の中身を最後まで確認する必要があるのです。
先程の例のように配列の長さが4だとすると、4回配列の中身を確認する必要があります。
この場合の計算量を漸近記法を使って表現してみましょう。入力の大きさは大体配列の大きさ N に等しいので、\(\Theta (N)\) となります。
最善の時(best case)
最善の時を考えてみましょう。計算量の下限(下界)を考えることになります。これによって、少なくともどれだけ時間がかかるかというのを見積もることができます。
線形探索の例では、配列の先頭に探したい要素が存在した時が最善になります。配列の先頭から探し始めるので、一番はじめに目的の数があればすぐに計算が終了するでしょう。
配列の長さがどれだけあっても(たとえ無限の長さであっても)、最善の時であれば 1 回だけ先頭を確認するだけで済みます。
この時の計算時間は、\(\Theta (1)\) となります。
最善の時があまり使われない理由としては、これが最悪の時や平均の時に比べて大きく値が異なることが多いからです。特殊なケースを考えるときにしか役に立ちません。
平均の時(average case)
平均の時間を考えてみましょう。最悪の計算量が大きくて時間がかかりそうでも、平均の計算量が小さければ実用では使える可能性があります。
最悪の計算量や最善の計算量は特殊な場合を考えればすぐに求めることができましたが、平均の計算量を見積もるのは大変です。全ての場合についての必要な計算時間を見積もり、平均を求める必要があります。
簡単のために、配列の中に目的の値が必ず存在するときを考えましょう。入力の大きさ(配列の長さ)が \(N\) として、このアルゴリズムに必要な平均計算量\(T(N)\)というのは、
$$T(N) = \frac{\sum^{N-1}_{0}{(i+1)}}{N} = \frac{N+1}{2}$$
となります。これを漸近記法を用いて表すと、\(T(N)=\Theta (N)\)とわかります。
このように、平均の計算量を見積もる際は、入力がどのような分布になっているかなどを知っておく必要もあります。よって、最悪の計算量のほうがよく用いられるのです。
ディスカッション
コメント一覧
平均計算量T(N)について、ΣN-1,0(i+1)とする意図は何でしょうか。
ΣN,1(i)の方が表記が簡略ではないかと考えます。
初学者です、質問失礼します。こういった最悪最善平均によって計算量を分ける場合、O記法でも良いのでしょうか。それともΘ記法の方が良いのでしょうか。