N – 木解説（AtCoder Typical DP Contest）

2020年3月31日2020年9月2日AtCoder階乗,剰余,動的計画法,数え上げ,逆元,木DP,部分木

問題へのリンク

Contents

1. 問題概要
- 1.1. 制約
2. 考え方
3. 解法
4. C++ での実装例
5. 参考：全方位木DP

問題概要

木が与えられる。辺が常に連結になるように木を描く。何通りの描き方があるか、mod 1,000,000,007 で求めよ。

制約

$2 \leq N \leq 1000 $

考え方

前提：木DPの考え方

俗に言う、木DP を用います。木DPでは以下のようなDPを基本に考えます。

dp[ v ] := 頂点 v を根とする部分木についての何かしらの値

それぞれの部分木から、ボトムアップ的に dp を計算していきます。以下のように、子を根とする部分木を組み合わせて新しい木をつくるイメージです。

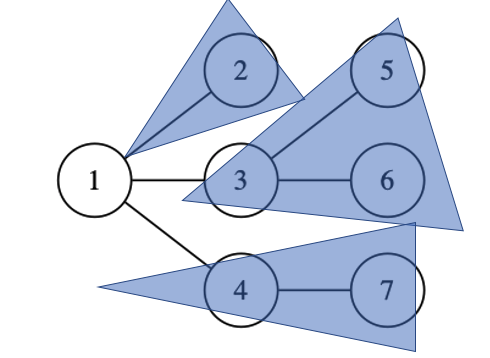
木DPの適用

以下のようなDPを考えます。

dp${}_r$ [ v ] := 頂点 v を根とする部分木の辺の描き方。ただし、辺は v に接続するものから描くとする。また、元々の木は r を根とする。

これの計算方法は少し分かりにくいので、具体例を見てみます。

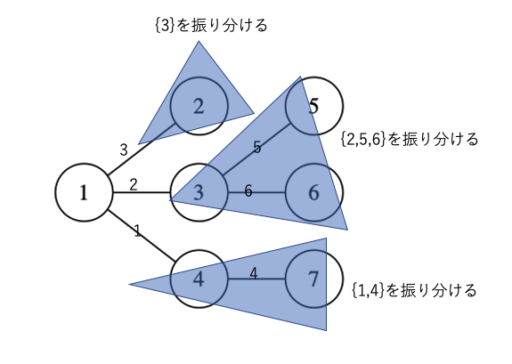
右の図で dp${}_1$[ 1 ] を求めることを考えてみましょう。

頂点2,3,4を根とする部分木の値は以下のように既に計算できているものとします。

dp${}_1$[ 2 ] = 1 通り
dp${}_1$[ 3 ] = 2通り
dp${}_1$[ 4 ] = 1通り

それぞれのcを根とする部分木の辺数に1（cからvへの辺）を加えた値は以下のようになります。

sub${}_1$[ 2 ] = 1 辺
sub${}_1$[ 3 ] = 3 辺
sub${}_1$[ 4 ] = 2 辺

この時描きたい辺は6辺あり、

1番目から6番目を、３つの部分木に振り分ける方法：$\frac{6!}{1!3!2!}$ 通り
それぞれの部分木で何通り描き方があるか：$1×2×1$ 通り

のようになります。よって全体では

$$1×2×1 × \frac{6!}{1!3!2!}$$

です。

それぞれの頂点を根として木DPを行う

先程は、「根とした頂点から辺を描き始める」ということを決めて木DPを行ったので、全ての描き方を数えるためには、それぞれの頂点について、木DPを繰り返さなくてはなりません。

その際に、同じものを重複して１回ずつ数えることになるので、最後に全体を2で割る必要があります。

解法

それぞれの頂点について、根 r とした時の木DPを以下のように行い、dp${}_r$ [ r ] の総和を2で割ったものが答えになります。

dp${}_r$ [ v ] := 頂点 v を根とする部分木の辺の描き方。ただし、辺は v に接続するものから描くとする。また、元々の木は r を根とする。

このようにすると、頂点 v の子 c を根とする部分木を組み合わせて以下のように計算することができます。cを根とする部分木の辺数に1（cからvへの辺）を加えたものを sub${}_r$[ c ] などとすると

dp${}_r$[ v ] =( $\prod_{c}$ dp${}_r$[ c ] ) × $( \sum_{c}$ sub${}_r$[ c ]$)!$ / $ (\prod_{c}($ sub${}_r$[ c ] $!))$

※ 実際に dp をforループなどで更新するのは大変なので、dfs などを利用して計算すると楽になります。

※ 階乗や階乗の逆元の計算は、前処理を行っておくことで $O(1)$ で計算することができます。

C++ での実装例

長いですが、前半部分はただのライブラリです。

剰余の計算が楽になるように ModInt 構造体を、階乗や階乗の逆元の計算が楽になるように、Comb構造体を利用しています。

#include <bits/stdc++.h>
using namespace std;

template <int mod>
struct ModInt {
    int val;
    ModInt() : val(0) {}
    ModInt(long long x) : val(x >= 0 ? x % mod : (mod - (-x) % mod) % mod) {}
    int getmod() { return mod; }
    ModInt &operator+=(const ModInt &p) {
        if ((val += p.val) >= mod) {
            val -= mod;
        }
        return *this;
    }
    ModInt &operator-=(const ModInt &p) {
        if ((val += mod - p.val) >= mod) {
            val -= mod;
        }
        return *this;
    }
    ModInt &operator*=(const ModInt &p) {
        val = (int)(1LL * val * p.val % mod);
        return *this;
    }
    ModInt &operator/=(const ModInt &p) {
        *this *= p.inverse();
        return *this;
    }
    ModInt operator-() const { return ModInt(-val); }
    ModInt operator+(const ModInt &p) const { return ModInt(*this) += p; }
    ModInt operator-(const ModInt &p) const { return ModInt(*this) -= p; }
    ModInt operator*(const ModInt &p) const { return ModInt(*this) *= p; }
    ModInt operator/(const ModInt &p) const { return ModInt(*this) /= p; }
    bool operator==(const ModInt &p) const { return val == p.val; }
    bool operator!=(const ModInt &p) const { return val != p.val; }
    ModInt inverse() const {
        int a = val, b = mod, u = 1, v = 0, t;
        while (b > 0) {
            t = a / b;
            swap(a -= t * b, b);
            swap(u -= t * v, v);
        }
        return ModInt(u);
    }
    ModInt pow(long long n) const {
        ModInt ret(1), mul(val);
        while (n > 0) {
            if (n & 1) ret *= mul;
            mul *= mul;
            n >>= 1;
        }
        return ret;
    }
    friend ostream &operator<<(ostream &os, const ModInt &p) { return os << p.val; }
    friend istream &operator>>(istream &is, ModInt &a) {
        long long t;
        is >> t;
        a = ModInt<mod>(t);
        return (is);
    }
    static int get_mod() { return mod; }
};
const int MOD = 1000000007;  // if inv is needed, this shold be prime.
using modint = ModInt<MOD>;

/* Comb：modintで二項係数を計算する構造体
    前処理：O(n)
    二項係数の計算：O(1)
    制約：
        n<=10^7
        k<=10^7
        p(mod)は素数
*/
template <class T>
struct Comb {
    vector<T> fact_, fact_inv_, inv_;
    // Comb() {}
    Comb(int SIZE) : fact_(SIZE, 1), fact_inv_(SIZE, 1), inv_(SIZE, 1) { init(SIZE); }
    void init(int SIZE) {
        fact_.assign(SIZE, 1), fact_inv_.assign(SIZE, 1), inv_.assign(SIZE, 1);
        int mod = fact_[0].getmod();
        for (int i = 2; i < SIZE; i++) {
            fact_[i] = fact_[i - 1] * i;
            inv_[i] = -inv_[mod % i] * (mod / i);
            fact_inv_[i] = fact_inv_[i - 1] * inv_[i];
        }
    }
    T nCk(int n, int k) {
        assert(!(n < k));
        assert(!(n < 0 || k < 0));
        return fact_[n] * fact_inv_[k] * fact_inv_[n - k];
    }
    T nHk(int n, int k) {
        assert(!(n < 0 || k < 0));
        return nCk(n + k - 1, k);
    }
    T fact(int n) {
        assert(!(n < 0));
        return fact_[n];
    }
    T fact_inv(int n) {
        assert(!(n < 0));
        return fact_inv_[n];
    }
    T inv(int n) {
        assert(!(n < 0));
        return inv_[n];
    }
};
Comb<modint> comb(10000);

struct Edge {
    int to;
};
using Graph = vector<vector<Edge>>;
using ll = long long;
using P = pair<modint, ll>;  // first:dpの値、 second:subの値
// 深さ優先探索
vector<bool> seen;              // 既に見たことがある頂点か記録
P dfs(const Graph &G, int v) {  // 頂点vを根とする部分木について、塗り方と辺のサイズを返す
    seen[v] = true;
    vector<P> ch;
    for (auto e : G[v]) {
        if (!seen[e.to]) {  // 訪問済みでなければ探索
            ch.push_back(dfs(G, e.to));
        }
    }
    P ret = P(modint(1), 0);
    if (ch.size() != 0) {
        for (auto c : ch) {
            ret.first *= c.first;                  // dp[c]をかける
            ret.first *= comb.fact_inv(c.second);  //sub[c]の階乗で割る
            ret.second += c.second;                // sub[c]の総和の階乗をかける
        }
        ret.first *= comb.fact(ret.second);
    }
    ret.second += 1;  // v の親への辺
    return ret;
}

int main() {
    int N;
    cin >> N;
    Graph G(N);
    for (int i = 0; i < N - 1; i++) {
        int a, b;
        cin >> a >> b;
        a--, b--;
        G[a].push_back({b});
        G[b].push_back({a});
    }

    modint ans = 0;
    for (int r = 0; r < N; r++) {  // ｒを根とした根付き木として見る
        seen.assign(N, false);     // 初期化
        ans += dfs(G, r).first;    // dp[r] を加える
    }
    cout << ans / 2 << endl;  // 二重に数えているので2で割る
    return 0;
}

参考：全方位木DP

頂点数が多い場合でも、全方位木DPと呼ばれる動的計画法を用いることで、$O(N)$ で求めることができます。

先程は各頂点ごとに木DPを行いましたが、同じ部分木が何度も登場するのでその分を上手く再利用してやることができます。

#include <bits/stdc++.h>
using namespace std;

template <int mod>
struct ModInt {
    int val;
    ModInt() : val(0) {}
    ModInt(long long x) : val(x >= 0 ? x % mod : (mod - (-x) % mod) % mod) {}
    int getmod() { return mod; }
    ModInt &operator+=(const ModInt &p) {
        if ((val += p.val) >= mod) {
            val -= mod;
        }
        return *this;
    }
    ModInt &operator-=(const ModInt &p) {
        if ((val += mod - p.val) >= mod) {
            val -= mod;
        }
        return *this;
    }
    ModInt &operator*=(const ModInt &p) {
        val = (int)(1LL * val * p.val % mod);
        return *this;
    }
    ModInt &operator/=(const ModInt &p) {
        *this *= p.inverse();
        return *this;
    }
    ModInt operator-() const { return ModInt(-val); }
    ModInt operator+(const ModInt &p) const { return ModInt(*this) += p; }
    ModInt operator-(const ModInt &p) const { return ModInt(*this) -= p; }
    ModInt operator*(const ModInt &p) const { return ModInt(*this) *= p; }
    ModInt operator/(const ModInt &p) const { return ModInt(*this) /= p; }
    bool operator==(const ModInt &p) const { return val == p.val; }
    bool operator!=(const ModInt &p) const { return val != p.val; }
    ModInt inverse() const {
        int a = val, b = mod, u = 1, v = 0, t;
        while (b > 0) {
            t = a / b;
            swap(a -= t * b, b);
            swap(u -= t * v, v);
        }
        return ModInt(u);
    }
    ModInt pow(long long n) const {
        ModInt ret(1), mul(val);
        while (n > 0) {
            if (n & 1) ret *= mul;
            mul *= mul;
            n >>= 1;
        }
        return ret;
    }
    friend ostream &operator<<(ostream &os, const ModInt &p) { return os << p.val; }
    friend istream &operator>>(istream &is, ModInt &a) {
        long long t;
        is >> t;
        a = ModInt<mod>(t);
        return (is);
    }
    static int get_mod() { return mod; }
};
const int MOD = 1000000007;  // if inv is needed, this shold be prime.
using modint = ModInt<MOD>;

/* Comb：modintで二項係数を計算する構造体
    前処理：O(n)
    二項係数の計算：O(1)
    制約：
        n<=10^7
        k<=10^7
        p(mod)は素数
*/
template <class T>
struct Comb {
    vector<T> fact_, fact_inv_, inv_;
    // Comb() {}
    Comb(int SIZE) : fact_(SIZE, 1), fact_inv_(SIZE, 1), inv_(SIZE, 1) { init(SIZE); }
    void init(int SIZE) {
        fact_.assign(SIZE, 1), fact_inv_.assign(SIZE, 1), inv_.assign(SIZE, 1);
        int mod = fact_[0].getmod();
        for (int i = 2; i < SIZE; i++) {
            fact_[i] = fact_[i - 1] * i;
            inv_[i] = -inv_[mod % i] * (mod / i);
            fact_inv_[i] = fact_inv_[i - 1] * inv_[i];
        }
    }
    T nCk(int n, int k) {
        assert(!(n < k));
        assert(!(n < 0 || k < 0));
        return fact_[n] * fact_inv_[k] * fact_inv_[n - k];
    }
    T nHk(int n, int k) {
        assert(!(n < 0 || k < 0));
        return nCk(n + k - 1, k);
    }
    T fact(int n) {
        assert(!(n < 0));
        return fact_[n];
    }
    T fact_inv(int n) {
        assert(!(n < 0));
        return fact_inv_[n];
    }
    T inv(int n) {
        assert(!(n < 0));
        return inv_[n];
    }
};

Comb<modint> comb(10000);

/* Rerooting: 全方位木 DP
    問題ごとに以下を書き換える
    - 型DPと単位元
    - 型DPに対する二項演算 fd
    - まとめたDPを用いて新たな部分木のDPを計算する fr
    計算量: O(N)
*/
struct Rerooting {
    /* start 問題ごとに書き換え */
    struct DP {  // DP の型
        modint dp;
        int s;
        DP(modint dp_, int s_) : dp(dp_), s(s_) {}
    };
    const DP unit_dp = DP(modint(1), 0);                                              // 単位元はしっかり定義する(末端でもfrされるので注意)
    function<DP(DP, DP, long long)> fd = [](DP dp_cum, DP d, long long cost) -> DP {  // d:辺eに対応する部分木のdpの値  cost:eのコスト
        int n = dp_cum.s + d.s;
        return DP(dp_cum.dp * d.dp * comb.nCk(n, d.s), n);
    };
    function<DP(DP)> fr = [](DP d) -> DP {  // まとめたDPを用いて、新たな部分木のDPを計算する
        return DP(d.dp, d.s + 1);
    };
    /* end 問題ごとに書き換え */

    // グラフの定義
    struct Edge {
        int from;
        int to;
        long long cost;
    };
    using Graph = vector<vector<Edge>>;

    vector<vector<DP>> dp;  // dp[v][i]: vから出るi番目の有向辺に対応する部分木のDP
    vector<DP> ans;         // ans[v]: 頂点vを根とする木の答え
    Graph G;

    Rerooting(int N) : G(N) {
        dp.resize(N);
        ans.assign(N, unit_dp);
    }

    void add_edge(int a, int b, long long c = 1) {
        G[a].push_back({a, b, c});
    }
    void build() {
        dfs(0);           // 普通に木DP
        bfs(0, unit_dp);  // 残りの部分木に対応するDPを計算
    }

    DP dfs(int v, int p = -1) {  // 頂点v, 親p
        DP dp_cum = unit_dp;
        int deg = G[v].size();
        dp[v] = vector<DP>(deg, unit_dp);
        for (int i = 0; i < deg; i++) {
            int u = G[v][i].to;
            if (u == p) continue;
            dp[v][i] = dfs(u, v);
            dp_cum = fd(dp_cum, dp[v][i], G[v][i].cost);
        }
        return fr(dp_cum);
    }
    void bfs(int v, const DP &dp_p, int p = -1) {
        int deg = G[v].size();
        for (int i = 0; i < deg; i++) {  // 前のbfsで計算した有向辺に対応する部分木のDPを保存
            if (G[v][i].to == p) dp[v][i] = dp_p;
        }

        vector<DP> dp_l(deg + 1, unit_dp), dp_r(deg + 1, unit_dp);  // 累積的なDP
        for (int i = 0; i < deg; i++) {
            dp_l[i + 1] = fd(dp_l[i], dp[v][i], G[v][i].cost);
        }
        for (int i = deg - 1; i >= 0; i--) {
            dp_r[i] = fd(dp_r[i + 1], dp[v][i], G[v][i].cost);
        }
        ans[v] = fr(dp_l[deg]);
        for (int i = 0; i < deg; i++) {
            int u = G[v][i].to;
            if (u == p) continue;
            bfs(u, fr(fd(dp_l[i], dp_r[i + 1], 0)), v);  // 累積同士のfdなので、edgeは適当に
        }
    }
};

int main() {
    int N;
    cin >> N;
    Rerooting reroot(N);
    for (int i = 0; i < N - 1; i++) {
        int u, v;
        cin >> u >> v;
        u--, v--;
        reroot.add_edge(u, v);
        reroot.add_edge(v, u);
    }
    reroot.build();

    modint ans = (0);
    for (int i = 0; i < N; i++) {
        ans += reroot.ans[i].dp;
    }
    cout << ans / 2 << endl;
}

2020年9月2日AtCoder階乗,剰余,動的計画法,数え上げ,逆元,木DP,部分木

ディスカッション

コメント一覧

まだ、コメントがありません