区間の和を求めるアルゴリズム(区間の更新なし)
要素数 N の数列 \(\{a_0, a_1, a_2, \cdots, a_{N-1}\}\) が与えられた時に、区間 [L, R) の和を求めるアルゴリズムについてです。
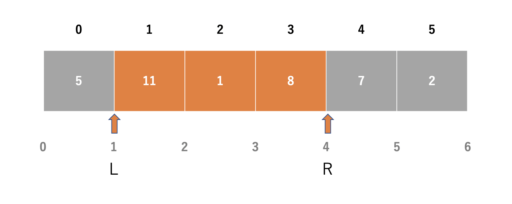
アルゴリズム
単純なアルゴリズム(前処理なし):
- \(a_L + a_{L+1} + \cdots + a_{R-1}\) を計算する
効率的なアルゴリズム(前処理あり):
- 前処理
- \(S_{i+1} = a_0 + a_1 + a_2+ \cdots + a_i \) となる、累積和 \(\{S_0, S_1, S_2, \cdots, S_N\}\) を求めておく
- クエリ(\(a_L + a_{L+1} + a_{L+2} + \cdots + a_{R-1}\) を求める)
- \( S_{R} – S_{L} \) を計算する
※ 前処理では \(S_{i+1} = S_i + a_i\) などとすると高速に計算ができます。
※ クエリでは \( S_{R} – S_{L} = a_L + a_{L+1} + \cdots + a_{R-1}\) となることを利用しています。
計算量
- 単純なアルゴリズム
- 前処理:なし
- クエリ:\(O(N)\)
- 効率的なアルゴリズム(前処理あり)
- 前処理:\(O(N)\)
- クエリ:\(O(1)\)
単純なアルゴリズムでは、区間に比例した回数足し算をしなければなりませんが、累積和を利用すると 1 回の引き算で計算ができます。
C++ での実装例(効率的なアルゴリズム)
#include <bits/stdc++.h>
using namespace std;
// 前処理を行う
void pre_process(vector<int> const &a, vector<int> &S) {
int n = (int)a.size();
S.assign(n + 1, 0);
for (int i = 0; i < n; i++) {
S[i + 1] = S[i] + a[i];
}
}
// [i,j) の区間和を求める
int query(int i, int j, vector<int> const &S) {
return S[j] - S[i];
}
int main() {
vector<int> a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
vector<int> S;
pre_process(a, S);
cout << query(1, 3, S) << endl; // 2+3 = 5
cout << query(2, 7, S) << endl; // 3+4+5+6+7 = 25
return 0;
}
累積和の気持ち
累積和とは
累積和は、「始めから i 番目までの和を前処理で計算したもの」です。つまり、「区間 [0, i) の和を全ての i について計算したもの」とも言えます。
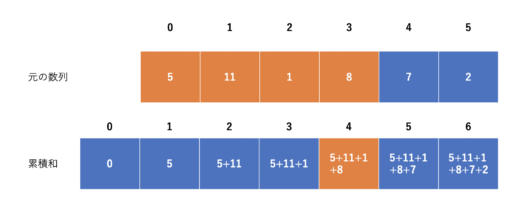
この累積和は、先程述べた通り、
- 1つあたり \(O(1)\)、全体で \(O(N)\) で高速に計算できる
- 累積和を利用して、任意の区間和が \(O(1)\) で求めることができる
という利点があります。
累積和は高速に計算できる
i 番目までの累積和が分かっていれば、i+1 番目の累積和というのは簡単に求めることができます。
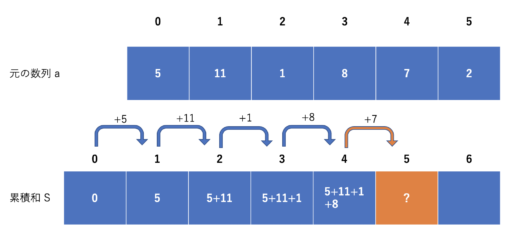
区間 [0, 4) の累積和を \(S_4\) などと表すようにしましょう。すると上の図のように、
\begin{align}
S_5 &= (5+11+1+8) + 7 \\
&= S_4 + a_4
\end{align}
となって、\(S_5\) は \(S_4\) を用いることで \(O(1)\) で計算することができます。
つまり、全体としては以下のような順番で計算すれば \(O(N)\) になります。
- \(S_0 = 0\)
- \(S_1 = S_0 + a_0\)
- \(S_2 = S_1 + a_1\)
- \(S_3 = S_2 + a_2\)
- …
- \(S_{i+1} = S_i + a_i\)
- …
- \(S_{N} = S_{N-1} + a_{N-1}\)
プログラムで書けば以下のようにすれば良いです。
// 前処理を行う
void pre_process(vector<int> const &a, vector<int> &S) {
int n = (int)a.size();
S.assign(n + 1, 0);
for (int i = 0; i < n; i++) {
S[i + 1] = S[i] + a[i];
}
}
累積和を用いると区間和が簡単に求まる
結論から言うと、区間 [L, R) の和は、累積和を用いると以下のように計算ができます。
- 区間 [L, R) の和 = \(S_R – S_L\)
数式を追って確かめてみましょう。まず、累積和は
- \(S_L\) = 区間 [0, L) の和 = \(a_0 + a_{1} + a_{2} + \cdots + a_{L-1}\)
- \(S_R\) = 区間 [0, R) の和 = \(a_0 + a_{1} + a_{2} + \cdots + a_{L-1} + a_{L}+ \cdots + a_{R-1}\)
となるので、
- \(S_R – S_L\) = \(a_L + a_{L+1} + a_{L+2} + \cdots + a_{R-1}\) = 区間 [L, R) の和
となり確かめられました。
コードでは以下のようになります。
// [i,j) の区間和を求める
int query(int i, int j, vector<int> const &S) {
return S[j] - S[i];
}
具体例
実際に区間 [1, 4) の区間和を累積和で求めてみましょう。
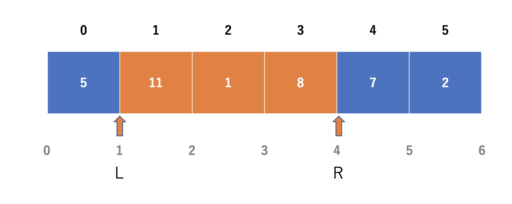
前処理して累積和を求めると、\(S_R\) は以下のようになります。
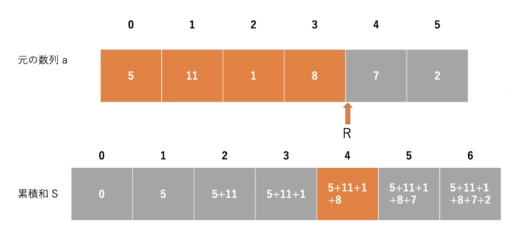
\(S_L\) は以下のようになります。
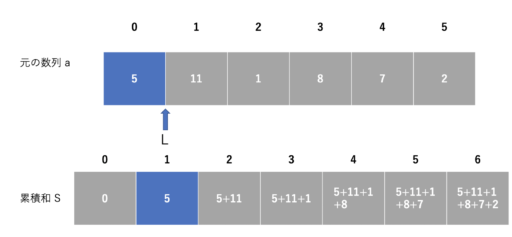
2つの差を考えると、ちょうど以下の部分になり、求めたいものが計算できます。

参考
二次元の区間和の場合
二次元の区間和を求める場合でも、同様に累積和を用いることで高速にクエリが処理できます。
区間の更新がある場合
数列を途中で変更するなどの「更新」があった場合は、累積和を計算し直す必要があるので逆に非効率になります。
そのような場合は、セグメント木や BIT などのデータ構造を用いると、
- 更新:\(O(\log N)\)
- クエリ:\(O(\log N)\)
で処理ができます。
ディスカッション
コメント一覧
まだ、コメントがありません