[AtCoder] ABC152 F – Tree and Constraints (600点)
問題概要
N頂点の木がある。辺を白か黒で塗るとき、以下のような制約をM個満たすような塗り方は何通りか?
制約 i:頂点 \(u_i\) と頂点 \(v_i\) を繋ぐパス上に、黒く塗られた辺が1つ以上存在する
制約
\begin{align}
&2 \leq N \leq 50 \\
&1 \leq M \leq min(20, N(N-1)/2)
\end{align}
考え方
「黒く塗られた辺が1つ以上」という条件のままでは、どのように考えていいか良くわかりません。「〜1つ以上」と言われたときは、その余事象を考えると条件がシンプルになることが多いです。
よって余事象を考えると問題は以下のように言い換えられます。
以下のようなM個の条件を1つも満たさない塗り方は何通りか?
¬制約 i:頂点 \(u_i\) と頂点 \(v_i\) を繋ぐパス上は全て白である
白になる辺の数が C 個と分かっていたら、他の辺の塗り方は自由なので \(2^{N – 1 – C}\)通りと簡単に求めることが可能です。
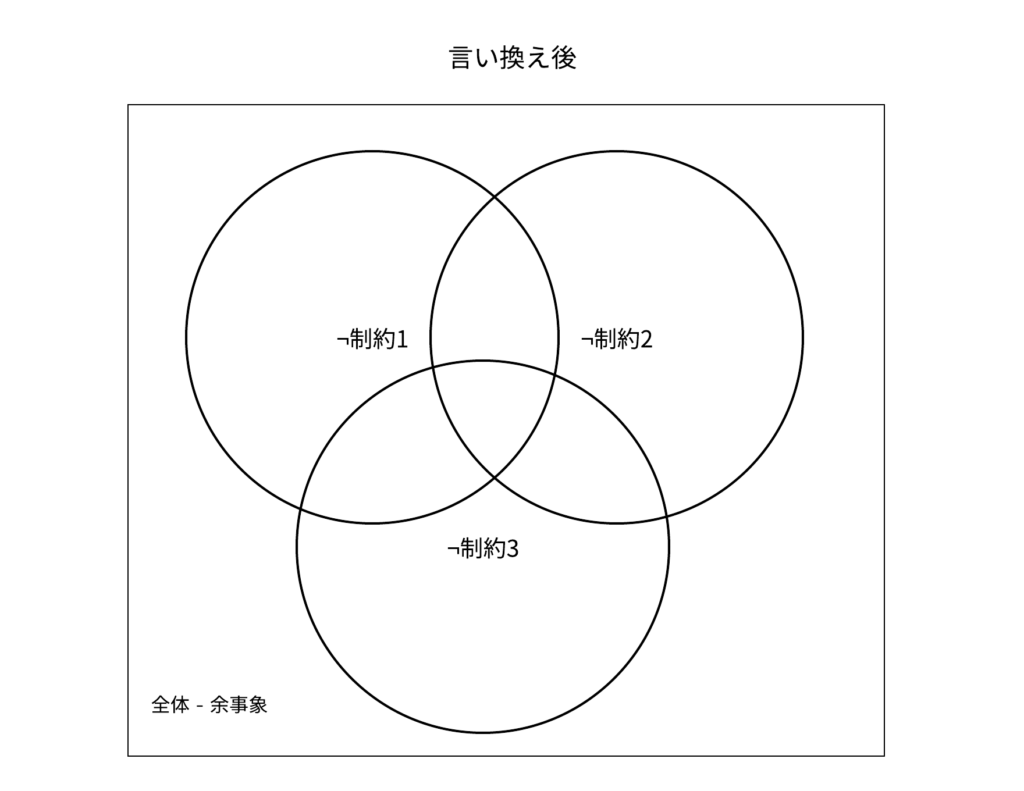
ベン図で考えると、全ての円の外側の部分(全体 – 余事象)が答えになります。このような状況では、余事象の部分(円の内側の範囲全て)が何通りかを求めるのに「包除原理」と呼ばれるものを使うことができます。
¬制約 をいくつか選んで、選んだ ¬制約 を全てを満たすときの塗り方を数えるとします。選んだ ¬制約 の数を k とすると、
- k が偶数ならその部分を足す
- k が奇数ならその部分を引く
ということをすると、最終的に「全体 – 余事象」を求めることができます(0の時は全体)。制約が2つや3つの場合で確かめてみてください。
¬制約 の選び方は\(2^M\)通りあるので、1つずつ計算すれば時間内に計算が可能です。
解き方
大まかな手順は以下の通りです。
- 制約ごとに、頂点 \(u_i\) と頂点 \(v_i\) を繋ぐパス上の辺を求めておく
- 包除原理によって、\(2^M\)通りの計算を行い、「全体 – 余事象」を求める
まずは制約ごとに、白くなるべき辺の場所を求めておきます。求め方はいくつかありますが、深さ優先探索で求める方法や、LCA(最近共通祖先)を使って求める方法などがあります。後で計算しやすくするために bit で管理しておくと良いです(白くなる辺のbit を立てておくなど)。
そして、包除原理で計算を行えば良いです。¬制約 の選び方は bit全探索によって全ての選び方を列挙することができます(bit が立っているとき、その制約を選ぶことにするなど)。
白くなる辺の管理に bit を使い、包除原理でも bit全探索を行うので、bit の扱いに慣れていないと難しく感じるでしょう。
解答例
深さ優先探索を用いた例
公式の解説とは違いますが、LCAのライブラリを作っていない人はこちらのほうが簡単です。
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); i++)
#define ALL(obj) begin(obj), end(obj)
using namespace std;
using ll = long long;
using ull = unsigned long long;
struct Edge {
long long to, id;
};
using Graph = vector<vector<Edge>>;
vector<int> path;
bool dfs(const Graph &G, int u, int v, int p) {
if (u == v) {
return true;
}
for (auto e : G[u]) {
if (e.to != p) {
if (dfs(G, e.to, v, u)) {
path.push_back(e.id);
return true;
}
}
}
return false;
}
int main() {
int N;
cin >> N;
Graph G(N);
rep(i, N - 1) {
int a, b;
cin >> a >> b;
a--, b--;
G[a].push_back({b, i});
G[b].push_back({a, i});
}
int M;
cin >> M;
// 制約ごとに、白くなる辺を入れておく
vector<ll> cons(M);
rep(i, M) {
int u, v;
cin >> u >> v;
u--, v--;
path = vector<int>();
dfs(G, u, v, -1); // 制約ごとに、白くなる辺をDFSで見つけ、pathに格納する
for (auto e : path) {
cons[i] |= 1LL << e;
}
}
// 包除原理
ll ans = 0;
rep(bit, 1LL << M) {
ll eset = 0;
rep(i, M) {
if (bit & (1LL << i)) {
eset |= cons[i];
}
}
int white = __builtin_popcountll(eset); // 白くなるべき辺の数
ll num = 1LL << (N - 1 - white);
if (__builtin_popcountll(bit) % 2 == 0) { // 制約が偶数か奇数か
ans += num;
} else {
ans -= num;
}
}
cout << ans << endl;
return 0;
}
LCAを用いた例
LCAを用いると、2頂点間の距離を\(O(logN)\)で求めることができます。これにより、2頂点を繋ぐパス上にある点 a が存在するかどうかも\(O(logN)\)で求めることができます。
パス上に辺が存在するかは、パス上に辺の両端が存在することと同値です。
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); i++)
#define ALL(obj) begin(obj), end(obj)
using namespace std;
using ll = long long;
using ull = unsigned long long;
struct Edge {
long long to, id;
};
using Graph = vector<vector<Edge>>;
/* LCA(G, root): 木 G に対する根を root として Lowest Common Ancestor を求める構造体
query(u,v): u と v の LCA を求める。計算量 O(logn)
前処理: O(nlogn)時間, O(nlogn)空間
*/
struct LCA {
vector<vector<int>> parent; // parent[k][u]:= u の 2^k 先の親
vector<int> depth; // root からの深さ
LCA(const Graph &G, int root = 0) { init(G, root); }
void init(const Graph &G, int root = 0) {
int V = G.size();
int K = 1;
while ((1 << K) < V) K++;
parent.assign(K, vector<int>(V, -1));
depth.assign(V, -1);
dfs(G, root, -1, 0); // initialization of parent[0] & depth
// initialization of parent
for (int k = 0; k + 1 < K; k++) {
for (int v = 0; v < V; v++) {
if (parent[k][v] < 0) {
parent[k + 1][v] = -1;
} else {
parent[k + 1][v] = parent[k][parent[k][v]];
}
}
}
}
void dfs(const Graph &G, int v, int p, int d) {
parent[0][v] = p;
depth[v] = d;
for (auto e : G[v]) {
if (e.to != p) dfs(G, e.to, v, d + 1);
}
}
int query(int u, int v) {
if (depth[u] > depth[v]) swap(u, v);
int K = parent.size();
for (int k = 0; k < K; k++) {
if ((depth[v] - depth[u]) >> k & 1) {
v = parent[k][v];
}
}
if (u == v) return u;
for (int k = K - 1; k >= 0; k--) {
if (parent[k][u] != parent[k][v]) {
u = parent[k][u];
v = parent[k][v];
}
}
return parent[0][u];
}
int dist(int u, int v) { return depth[u] + depth[v] - 2 * depth[query(u, v)]; }
bool is_in(int u, int v, int a) { return dist(u, a) + dist(a, v) == dist(u, v); }
};
int main() {
int N;
cin >> N;
Graph G(N);
vector<pair<int, int>> edges;
rep(i, N - 1) {
int a, b;
cin >> a >> b;
a--, b--;
G[a].push_back({b, i});
G[b].push_back({a, i});
edges.push_back({a, b});
}
LCA lca(G, 0);
int M;
cin >> M;
// 制約ごとに、白くなる辺を入れておく
vector<ll> cons(M);
rep(i, M) {
int u, v;
cin >> u >> v;
u--, v--;
rep(j, N - 1) { // その辺が白くなるべきか全探索
int a = edges[j].first;
int b = edges[j].second;
if (lca.is_in(u, v, a) && lca.is_in(u, v, b)) {
cons[i] |= 1LL << j;
}
}
}
// 包除原理
ll ans = 0;
rep(bit, 1LL << M) {
ll eset = 0;
rep(i, M) {
if (bit & (1LL << i)) {
eset |= cons[i];
}
}
int white = __builtin_popcountll(eset);
ll num = 1LL << (N - 1 - white);
if (__builtin_popcountll(bit) % 2 == 0) {
ans += num;
} else {
ans -= num;
}
}
cout << ans << endl;
return 0;
}
ディスカッション
コメント一覧
まだ、コメントがありません