グラフの2頂点が同じ連結成分に属するか判定するアルゴリズム
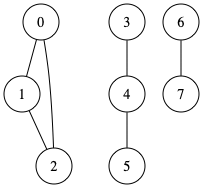
連結成分とは、「任意の2頂点間にパスが存在するような部分グラフのうち極大なもの」のことを言います。
グラフ \(G=(V,E)\) 上の2頂点 \(u,v\) が同じ連結成分に属しているか判定するアルゴリズムについてです。
アルゴリズム
単純なアルゴリズム(前処理なし):
- 片方の頂点 \(u\) から DFSやBFSで到達できる点を全て探索して、\(v\) がそこに含まれているか判定する
効率的なアルゴリズム(DFS or BFS を使用):
- 前処理
- 「未探索」の頂点について以下を行う
- DFS or BFS で、同じ連結成分に含まれる全ての頂点に連結成分に固有な番号を記録しておく
- 「未探索」の頂点について以下を行う
- クエリ(\(u,v\) が同じ連結成分か判定)
- 前処理で記録した番号が、2頂点で等しいか比較する。等しければ同じ連結成分に属する。
効率的なアルゴリズム(Union-Find Tree を使用):
- 前処理(頂点を木のノードに対応させる)
- パスがあれば、2頂点を含む木をそれぞれ併合する(union)
- クエリ(\(u,v\) が同じ連結成分か判定)
- 2頂点が同じ集合(木)に属するか判定する
※ Union-Find Tree は素集合系を扱うデータ構造で、連結かどうかを調べるのによく用いられます。(参考:Union-Find Tree を理解する!素集合系を扱うデータ構造)
計算量
- 単純なアルゴリズム(前処理なし)
- 前処理:なし
- 判定:\(O(|V|+|E|)\)
- 効率的なアルゴリズム(DFS or BFS)
- 前処理:\(O(|V|+|E|)\)
- 判定:\(O(1)\)
- 効率的なアルゴリズム(Union-Find Tree )
- 前処理:\(O(\alpha(|V|)×|E|)\)
- 判定:\(O(\alpha(|V|))\)
Union-Find Treeを用いる場合は、1回の併合と判定にならし \(O(\alpha(|V|))\) だけかかります。
よって前処理は \(O(\alpha(|V|)×|E|)\) となりますが、\(\alpha(|V|)\) はかなり小さい数なので DFS や BFS を用いた効率的なアルゴリズムと大きくは変わりません。
C++ での実装例
単純なアルゴリズム
頂点数 V 、辺の数 E のグラフについて、頂点 s から頂点 t に到達できるかを探索するプログラムの実装例です。到達できれば 'yes’ と出力し、到達できなければ 'no’ と出力します。
入力形式は以下の通りです。V, E, s, t に加えて、ai から bi への無向辺が E 個与えられます。
V E
s t
a1 b1
a2 b2
…
aE bE
#include <bits/stdc++.h>
using namespace std;
using Graph = vector<vector<int>>;
// 深さ優先探索
vector<bool> seen; // 既に見たことがある頂点か記録
void dfs(const Graph &G, int v) {
seen[v] = true;
for (auto next : G[v]) {
if (!seen[next]) { // 訪問済みでなければ探索
dfs(G, next);
}
}
}
int main() {
int V, E;
cin >> V >> E;
int s, t;
cin >> s >> t;
Graph G(V);
for (int i = 0; i < E; i++) {
int a, b;
cin >> a >> b;
G[a].push_back({b});
G[b].push_back({a});
}
seen.assign(V, false); // 初期化
dfs(G, s);
if (seen[t]) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
return 0;
}
効率的なアルゴリズム(DFS or BFS)
AOJ ALDS1_11_D Connected Components を解く実装例です。\(n\) 頂点と \(m\) 個の辺からなるグラフが与えられ、\(q\) 個のクエリに答えます。
#include <bits/stdc++.h>
using namespace std;
struct Edge {
int to;
};
using Graph = vector<vector<Edge>>;
// 深さ優先探索
vector<int> cc; // どの連結成分か記録
void dfs(const Graph &G, int v, int id) {
cc[v] = id;
for (auto e : G[v]) {
if (cc[e.to] == -1) { // 訪問済みでなければ探索
dfs(G, e.to, id);
}
}
}
int main() {
int n, m;
cin >> n >> m;
Graph G(n);
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
G[a].push_back({b});
G[b].push_back({a});
}
int q;
cin >> q;
vector<int> s(q), t(q);
for (int i = 0; i < q; i++) {
cin >> s.at(i) >> t.at(i);
}
cc.assign(n, -1); // 初期化
int id = 0;
for (int i = 0; i < n; i++) {
if (cc[i] == -1) {
dfs(G, i, id);
id++;
}
}
// id は連結成分の個数にもなっている
for (int i = 0; i < q; i++) {
if (cc[s[i]] == cc[t[i]]) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
}
return 0;
}
効率的なアルゴリズム(Union-Find Tree)
AOJ ALDS1_11_D Connected Components を解く実装例です。\(n\) 頂点と \(m\) 個の辺からなるグラフが与えられ、\(q\) 個のクエリに答えます。
Union-Find Tree のコードがあればそれを貼り付けるだけなので、先程よりも簡単に実装できます。
#include <bits/stdc++.h>
using namespace std;
/* UnionFind:素集合系管理の構造体(union by size)
isSame(x, y): x と y が同じ集合にいるか。 計算量はならし O(α(n))
unite(x, y): x と y を同じ集合にする。計算量はならし O(α(n))
treeSize(x): x を含む集合の要素数。
*/
struct UnionFind {
vector<int> size, parents;
UnionFind() {}
UnionFind(int n) { // make n trees.
size.resize(n, 0);
parents.resize(n, 0);
for (int i = 0; i < n; i++) {
makeTree(i);
}
}
void makeTree(int x) {
parents[x] = x; // the parent of x is x
size[x] = 1;
}
bool isSame(int x, int y) { return findRoot(x) == findRoot(y); }
void unite(int x, int y) {
x = findRoot(x);
y = findRoot(y);
if (size[x] > size[y]) {
parents[y] = x;
size[x] += size[y];
} else {
parents[x] = y;
size[y] += size[x];
}
}
int findRoot(int x) {
if (x != parents[x]) {
parents[x] = findRoot(parents[x]);
}
return parents[x];
}
int treeSize(int x) { return size[findRoot(x)]; }
};
int main() {
int n, m;
cin >> n >> m;
UnionFind uf(n);
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
uf.unite(a, b);
}
int q;
cin >> q;
vector<int> s(q), t(q);
for (int i = 0; i < q; i++) {
cin >> s.at(i) >> t.at(i);
}
for (int i = 0; i < q; i++) {
if (uf.isSame(s[i], t[i])) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
}
return 0;
}
ディスカッション
コメント一覧
まだ、コメントがありません