Ford-Fullkerson法による最大フローの値を求めるアルゴリズム
アルゴリズム
最大フローを求めるアルゴリズム(Ford-Fullkerson法):
- フロー \(f\) を 0 としてはじめる
- ソース(入口) からシンク(出口)までの増加可能経路 \(p\) が残余ネットワーク \(G_f\) に存在する間は以下を繰り返す
- フロー \(f\) を \(p\) に沿って増やす
- フロー \(f\) の流量 \(|f|\) を返す
※ 残余ネットワークは、「後どれだけフローを流せるか」を表す残余容量を重みとしたグラフのこと。
※ 増加可能経路は、正の容量を持つ辺のみからなる、ソースからシンクへのパスのこと。
※ フローの基本となる用語の説明はこちら
2. では深さ優先探索や幅優先探索などを用いて、以下のような増加可能経路を探します。
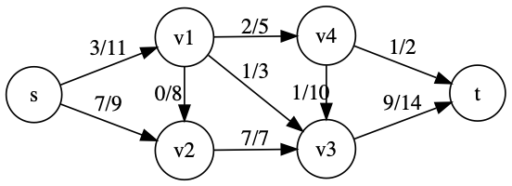
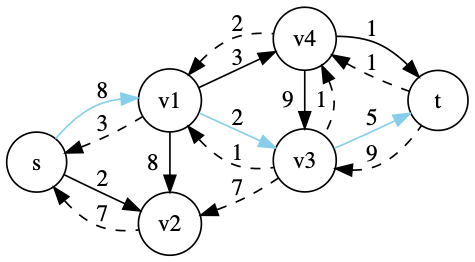
計算量
最大フローを \(f^*\) 、容量を整数とした時、計算量は以下のようになります。
- \(O( |f^*| × |E|)\)
フローを増加可能経路に沿って増やすごとに、フローの値は 1 以上増えていくので、繰り返しの回数は高々 \(|f*|\) 回です。
フローを増加可能経路に沿って増やすためには、深さ優先探索か幅優先探索を用いれば良いので、\(O(|E|)\) で計算を行うことができます。
実際は、一回ごとに増えるフローの値が 1 しかないことは少ないので、この見積もりよりも高速に動くことが多いです。
C++ での実装例
残余ネットワークを上手く更新していくために、辺を表す Edge 構造体と、グラフ(残余ネットワーク)を表す Graph 構造体を用いています。
template <class T>
struct Edge {
int rev, from, to; // rev:逆向きの辺の番号
T cap, original_cap;
Edge(int r, int f, int t, T c) : rev(r), from(f), to(t), cap(c), original_cap(c) {}
};
template <class T>
struct Graph {
vector<vector<Edge<T>>> G;
Graph(int n = 0) : G(n) {}
vector<Edge<T>>& operator[](int i) { return G[i]; }
const size_t size() const { return G.size(); }
Edge<T>& redge(Edge<T> e) { // 逆向きの辺を返す
return G[e.to][e.rev]; // 自己ループはないと仮定(あれば G[e.to][e.rev + 1] とする必要がある)
}
void add_edge(int from, int to, T cap) { // 有向辺を加える
G[from].push_back(Edge<T>((int)G[to].size(), from, to, cap));
G[to].push_back(Edge<T>((int)G[from].size() - 1, to, from, 0));
}
};
/* FordFulkerson: Ford-Fulkersonのアルゴリズムで最大流を求める構造体
max_flow(G,s,t):sからtへのグラフGの最大流を求める
副作用:G は最大流の残余ネットワークになる
計算量: O(|f*||E|) (f*:最大流) (この最悪ケースになることはほぼ無い)
*/
template <class T>
struct FordFulkerson {
const T INF = 1e9;
vector<int> used;
FordFulkerson(){};
T dfs(Graph<T>& G, int v, int t, T f) { // 増加可能経路を見つけて増加分のフローを返す
if (v == t) return f;
used[v] = true;
for (auto& e : G[v]) {
if (!used[e.to] && e.cap > 0) {
T d = dfs(G, e.to, t, min(f, e.cap));
if (d > 0) {
e.cap -= d;
G.redge(e).cap += d;
return d;
}
}
}
return 0;
}
T max_flow(Graph<T>& G, int s, int t) {
T flow = 0;
while (true) {
used.assign(G.size(), 0);
T f = dfs(G, s, t, INF); // f が増加分のフロー
if (f == 0) {
return flow;
} else {
flow += f;
}
}
return 0;
}
};
アルゴリズムの正当性
さきほどのアルゴリズムが正しく動作するのは、以下の定理によって分かります。
以下は全て同値となる。
1. \(f\) は \(G\) における最大フロー
2. 残余ネットワーク \(G_f\) は増加可能経路を含まない
3.\(G\) のカット \((S,T)\) が存在して、 \(|f| = c(S,T)\) を満たす(これは最小カットとなる)
この定理によれば、残余ネットワーク \(G_f\) は増加可能経路を含まないことと、\(f\) が \(G\) における最大フローとなることは必要十分です。
つまり、増加可能経路が無くなった時点で、その時のフローが最大であることが分かります。
練習問題
- AOJ GRL_6_A Maximum Flow:チェック用
ディスカッション
コメント一覧
“Ford-Fulkerson” のスペリングが一部間違っています…