フローネットワークの基礎と用語の定義
フロー
フローとフローネットワーク
関数 \(f : V×V \rightarrow \mathbb{R}\)で表現されるフローは、以下の特徴を持つ重み付き有向グラフ(フローネットワーク) \(G=(V,E)\) 上で定義されます。
・始点 \(s\) と終点 \(t\) が存在し、始点をソース・終点をシンクなどと呼ぶ
・容量 \(c(u,v)\) は非負
・逆向きの辺は含まない:\((u,v)\in E\) ならば \((v,u)\notin E\)
・自己ループは無い
また、フロー \(f\) は以下を満たします。
容量制限:全ての \(u,v \in V\) について、\(0 \leq f(u,v) \leq c(u,v)\)
フロー保存則:全ての \(u\in V \backslash \{s,t\}\) について、\(\sum_{v \in V}f(u,v) = \sum_{v\in V}f(v,u)\)
1つ目の容量制限は、フローが容量を超えないように流れる必要があることを表します。
2つ目のフロー保存則は、始点と終点以外では、入り込む量と出ていく量が等しいことを表しています。
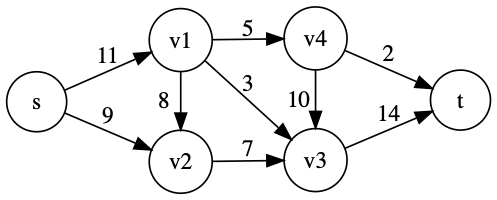
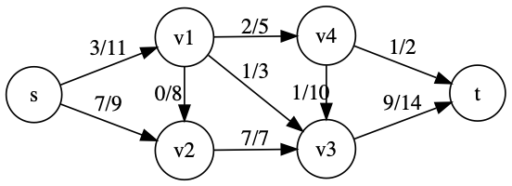
特徴をまとめると、
- 各辺のフローは容量を超えない
- (ソースとシンクを除く)各頂点へ入るフローの値と、出ていくフローの値は同じ
- ソース(入口) から出るフローの値と、シンク(出口)に入るフローの値は同じ
となります。
フローの値(流量)
フロー \(f\) の値 \(|f|\) を、始点から出るフローの合計と、始点に入り込むフローの合計の差として表すことにします。
$$ |f| = \sum_{v \in V}f(s,v) ~ – \sum_{v \in V}f(v,s) $$

※ 始点に入り込むフローを考えることは多く無いので、出るフローのみを考えれば良い場合が多いです。
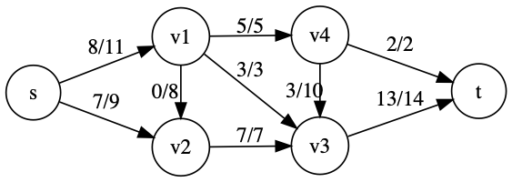
最大フロー
先程のフローの条件(容量制限・フロー保存則)を満たすものの中で、フローの値 \(|f|\) が最大となるものを、最大フロー などと言います。
残余ネットワークと増加可能経路
残余容量
フロー \(f\) に対して定義される以下の値を、残余容量と言います。
$$ c_f(u,v) := \left\{ \begin{array}{ll}
c(u,v) ~ – f(u,v) & ((u,v)\in E) \\
f(u,v) & ((v,u)\in E) \\
0 & (otherwise)
\end{array} \right. $$
\((u,v)\in E\) の場合を考えてみます。フローが定義されると、「あとどれくらいフローを流すことができるか」という値も \(c_f(u,v) = c(u,v) ~ – f(u,v)\) で定めることができます。
さらにこれを拡張して考えると、\((v,u)\in E\) の場合、「流したフローはどれくらいで、逆向きに押し返せる最大値はいくつか」という値も \(c_f(u,v) = f(u,v)\) で定めることができます。
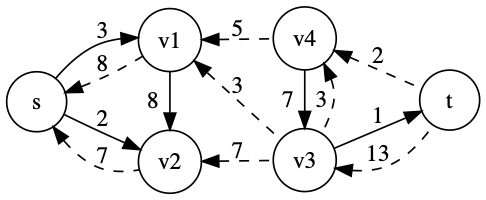
残余ネットワーク
残余容量自体を、容量として構築したネットワーク \(G_f = (V, E_f)\) を、残余ネットワークと呼びます。
「あとどれくらいフローを流すことができるか」や「どのくらい逆流できるか」が分かりやすくなります。

増加可能経路(増加道)
残余ネットワーク内で、ソース \(s\) からシンク \(t\) へのパスのうち、パス上の任意の辺 \((u,v)\) について
$$ 0 < c_f(u,v)$$
が成り立つようなパスを、増加可能経路(増加道)などと言います。
もう少し厳密にすると、増加可能経路 \((v_1, v_2, v_3, …, v_k)\) は以下を満たします。
・ \(v_1 = s\)
・ \(v_k = t\)
・ \(0 < c_f(v_i,v_{i+1})\)
増加可能経路があれば、追加でフローを流すことができると分かります。

ディスカッション
コメント一覧
まだ、コメントがありません