動的計画法(Dynamic Programming)入門
動的計画法とは
動的計画法(Dynamic Programming)とは、小さい部分問題を計算して記録しておき、より大きい問題を計算する際に利用する手法のことです。
以下のような特徴がありますが、抽象的なのでここではざっと眺める程度で構いません。
- 計算したい問題を、より小さい部分問題を利用して計算できる
- 部分問題が何度も出現する
- 部分問題の計算結果を保存しておけば再利用できる(無駄な計算をしなくても良い)
普通に計算すると同じ計算を何度も繰り返してしまい非効率であるようなアルゴリズムも、動的計画法を利用することで高速化することができます。
いくつか具体例を見ながら、動的計画法の概念に慣れていきましょう。
フィボナッチ数列の計算
以下のような、前2つの数を足していくような並びの数列をフィボナッチ数列といいます。
1, 1, 2, 3, 5, 8, 13, 21, …
漸化式で表すと以下の通りです。
$$ a_{n+2} = a_{n+1} + a_{n} $$
これの第 n 項を求める方法を考えてみましょう。
動的計画法を使わないで計算する場合
ナイーブに実装すると再帰関数を利用して以下のようになります。
int fib(int n) {
if (n <= 2) {
return 1;
} else {
return fib(n - 1) + fib(n - 2);
}
}
第 n 項を求めるために、第 n-1 項と第 n-2 項を再帰的に呼び出して計算する必要があります。つまり、fib(n) の計算のために、fib(n-1) と fib(n-2) という部分問題を解く必要があるのです。
実は、この部分問題は何度も登場することになり、同じ計算を何度も行っているため非効率です。第5項を求める場合を例として考えてみましょう。
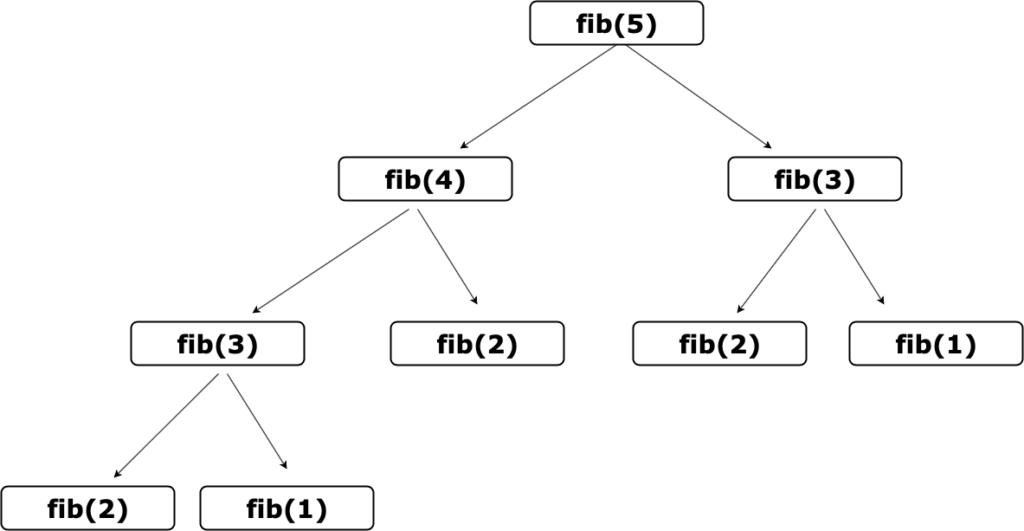
上の図を見てもらうとわかりますが、fib(5)の計算をする際に、fib(3)の計算を2回行っています。つまり、同じ計算を余分に 1 回行うことになります。
今回はfib(5)の計算なのでこの程度で済んでいますが、求めたいフィボナッチ数が大きくなればなるほど、その無駄が無視できない大きさにまでなってしまいます。
動的計画法を使う場合(メモ化再帰)
一度計算したfib(n)の結果を配列などに保存しておき、既に計算したことのある値だったら再利用することにしましょう。
これにより、無駄な計算が無くなって、かなりの高速化ができます。
int memo[100000];
int fib_dp(int n) {
if (n <= 2) {
return 1;
} else {
if (memo[n] != 0) { // 計算したことがある値だったら再利用
return memo[n];
} else {
memo[n] = fib_dp(n - 1) + fib_dp(n - 2); // 計算結果をメモに保存
return memo[n];
}
}
}
このような再帰関数によるトップダウン型の動的計画法の実装方法を、メモ化再帰などと言うことがあります。
動的計画法を使う場合(漸化式)
メモ化再帰は、再帰関数を使ってメモしていきましたが、直接配列の上で計算してしまっても構いません。
dp[ i ] := フィボナッチの第 i 項
となるよう、以下のように i が0からn-2の時まで更新してやります。
dp[ i+2 ] = dp[ i+1 ] + dp[ i ]
int dp[10000];
dp[1] = 1;
dp[2] = 1;
for (int i = 1; i < n - 1; i++) {
dp[i + 2] = dp[i + 1] + dp[i];
}
このような、漸化式を利用したボトムアップ型の動的計画法の実装方法もあります。
ナップサック問題
動的計画法を使う有名な問題です。以下のような問に答えます。
価値が \(v_i\) 、重さが \(w_i\) で表される荷物が N 個ある。重さ B を超えないようにナップサックに入れる時、選んだ荷物の価値の合計は最大でどれだけか?
ここでは、AtCoder Beginner Contest 032 D – ナップサック問題 のデータセット 2 に対応する部分点を得る解答を考えることとします。(つまり、N≦200 かつ全ての i(1≦i≦N) について 1≦wi≦1000 を満たす)
理解ができたら、問題の入力例と出力例を使って確認してみると良いでしょう。
動的計画法を使わない場合
動的計画法を使わないナイーブな実装を考えてみましょう。荷物の入れ方を全探索し、重さBを超えないもので価値が最大となる時を出力すれば良いです。
荷物の選び方は、それぞれの荷物に対して「入れる or 入れない」の2通りがあるので、全体で\(2^N\)通りあります。
これは再帰関数を用いて計算することができます。 i 番目の荷物を選択するかしないかで分岐させてください。
#include <bits/stdc++.h>
using namespace std;
int N, B;
int v[205], w[205];
long long knapsack_rec(int i, int b) { // i 番目まで選択して、残り容量は b
long long ret;
if (i == N) {
ret = 0;
} else if (b < w[i]) {
ret = knapsack_rec(i + 1, b);
} else {
long long use = knapsack_rec(i + 1, b - w[i]) + v[i]; // 入れる
long long no_use = knapsack_rec(i + 1, b); // 入れない
ret = max(use, no_use);
}
return ret;
}
int main() {
// 入力
cin >> N >> B;
for (int i = 0; i < N; i++) {
cin >> v[i] >> w[i];
}
cout << knapsack_rec(0, B) << endl; // 答えの出力
}
これも、部分問題が構造的に現れています。knapsack(i,b) の計算をする上で、knapsack(i + 1, b – w[i]) や knapsack(i + 1, b) といった部分問題を解く必要があります。
何も工夫をしなければ同じ部分問題を何度も計算することになるので、荷物の数Nが大きい場合、計算にかなりの時間がかかってしまいます。
動的計画法を使う場合(メモ化再帰)
先程のフィボナッチの例と同様に、動的計画法によって高速化させることができます。部分問題の計算結果を保存しておきましょう。
ナップサックのナイーブな再帰関数も、余計な計算があるので、メモ化再帰によって高速化ができます。結果を配列に保存しておき、2回目以降は再利用をしましょう。
#include <bits/stdc++.h>
using namespace std;
long long memo[205][200005];
int N, B;
int v[205], w[205];
long long knapsack_rec(int i, int b) {
if (memo[i][b] != 0) { // 既に計算したことがあるなら再利用
return memo[i][b];
}
long long ret;
if (i == N) {
ret = 0;
} else if (b < w[i]) {
ret = knapsack_rec(i + 1, b);
} else {
long long use = knapsack_rec(i + 1, b - w[i]) + v[i];
long long no_use = knapsack_rec(i + 1, b);
ret = max(use, no_use);
}
memo[i][b] = ret; // 結果をメモ
return ret;
}
int main() {
// 入力
cin >> N >> B;
for (int i = 0; i < N; i++) {
cin >> v[i] >> w[i];
}
cout << knapsack_rec(0, B) << endl; // 答えの出力
}
動的計画法を使う場合(漸化式)
漸化式を使って同じ問題をどのように表現すれば良いか考えてみましょう。先程のメモ化した配列を参考にして、
dp[ i ][ b ] := 残りの重さ(容量)が b 以上となる i 番目までの荷物の選び方で、最大となる価値の総和
というのを漸化式を用いて表現してみましょう。
仮に最適な選び方をしたとして、dp[ i+1 ][ b ] の値を考えてみましょう。
i 番目の荷物を使う時は dp[ i ][ b + w[ i ]]+v[ i ] が価値の総和の最大となり、使わない時は dp[ i ][ b ] となるはずです。
(残りの重さを考えていることに注意してください。i 番目の荷物を使う時は、残りが b+W[ i ] からW[ i ] だけ減って b になればよいはずです。)
よって漸化式は以下のようになります。
dp[ i+1 ][ b ] = max(dp[ i ][ b + w[ i ]]+v[ i ], dp[ i ][ b ])
#include <bits/stdc++.h>
using namespace std;
long long dp[205][200005];
int main() {
// 入力
int N, B;
cin >> N >> B;
vector<int> v(N), w(N);
for (int i = 0; i < N; i++) {
cin >> v.at(i) >> w.at(i);
}
// DP の計算
for (int i = 0; i <= N; i++) {
for (int b = B; b >= 0; b--) {
if (b + w[i] > B) {
dp[i + 1][b] = dp[i][b];
} else {
dp[i + 1][b] = max(dp[i][b + w[i]] + v[i], dp[i][b]);
}
}
}
cout << dp[N][0] << endl; // 答えの出力
}
求める答えは、 dp[N][0] になります。
ナップサックの漸化式的な解き方は他にも色々あります。以下のように残りの容量のかわりに、今まで入れた荷物の量とすることもできます。
dp[ i ][ b ] := i 番目までの荷物について、今までに入れた重さの総和が b 以下となるもので、価値の総和の最大値
ディスカッション
コメント一覧
漸化式の説明の中で「i 番目の荷物を使う時は dp[ i-1 ][ b – w[ i ]]+v[ i ] が価値の総和の最大となり、使わない時は dp[ i-1 ][ b ] となるはずです。」と書かれていますが、漸化式は
dp[ i ][ b ] = max(dp[ i-1 ][ b + w[ i ]]+v[ i ], dp[ i-1 ][ b ]になっています。(w[i]の符号が異なる)
間違いではありませんか?
符号が逆でした。ご指摘ありがとうございます!
修正させて頂きました。
すみません
dp[ i ][ b ] = max(dp[ i-1 ][ b + w[ i ]]+v[ i ], dp[ i-1 ][ b ])
のところですが、b + w[ i ]であってますか?b – w[ i ]ではなくて?
コメントありがとうございます!
結論からいうと、符号は間違っていません。
漸化式を用いた方では、
dp[i][b] := 残りの重さ(容量)がb以上となるi番目までの荷物の選び方で、最大となる価値の総和
というように考えています。
i番目の荷物を使う時は、残りが b+W[i] からW[i] だけ減って b になればよいはずです。
b-w[i] となるのは、
dp[i][b] := i 番目までの荷物について、今までに入れた重さの総和がb以下となるもので、価値の総和の最大値
というように考えた場合になるでしょう。
とはいえ、ソースコードも部分的にしかなく実験しにくいため、全体的に分かりにくかったと思います。
全体的に修正を加えて、参考となる問題を解く形に変更しました。