Nの約数の個数を求めるアルゴリズム

2020年3月26日2021年1月9日数学約数,素因数分解,約数の個数

素因数分解を用いることで、約数の個数を簡単に求めることができます。

アルゴリズム

※ 素因数分解のアルゴリズムに関してはこちらを参照

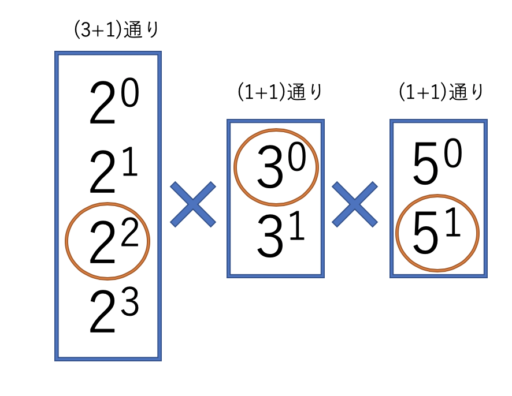
※ 例として、$120 = 2^3 × 3^1 × 5^1$ の約数の個数は、$(3+1)×(1+1)×(1+1) = 16$ となります。

※ 個数だけではなく、どんな約数があるか全列挙したい場合は、N の約数を全列挙するアルゴリズムを参照してください。

計算量

• 前処理なしのアルゴリズム
  • 前処理：なし
  • クエリ：$O(\sqrt{N})$
• SPF を利用した前処理ありのアルゴリズム
  • 前処理：$O(N \log \log N)$
  • クエリ：$O(\log N)$

素因数分解に $O(\sqrt{N})$ だけ時間がかかります。$O(N \log \log N)$ での前計算を許せば、SPF を利用して $O(\log{N})$ で素因数分解ができます。（詳細：素因数分解のアルゴリズム）

「指数に1を足して、すべてかけ合わせる」のには N の素因数の種類だけ計算することになるので $O(\log{N})$ 程度で抑えられ、素因数分解の計算量を超えません。

C++での実装例

以下は、標準入力から整数 N を受け取って、Nの約数の個数を出力するプログラムです。前処理なしでのアルゴリズムで実装しています。

#include <bits/stdc++.h>
using namespace std;

// 素因数分解
template <typename T>
map<T, T> prime_factor(T n) {
    map<T, T> ret;
    for (T i = 2; i * i <= n; i++) {
        T tmp = 0;
        while (n % i == 0) {
            tmp++;
            n /= i;
        }
        ret[i] = tmp;
    }
    if (n != 1) ret[n] = 1;
    return ret;
}

/*  divisor_num(n)
    入力：整数 n
    出力：nの約数の個数
    計算量：O(√n)
*/
template <typename T>
T divisor_num(T N) {
    map<T, T> pf = prime_factor(N);
    T ret = 1;
    for (auto p : pf) {
        ret *= (p.second + 1);
    }
    return ret;
}

long long N;

int main() {
    cin >> N;
    cout << divisor_num(N) << endl;
    return 0;
}

練習問題

• [AtCoder] ARC 034 C – 約数かつ倍数：単純に約数を全列挙するのは難しいです。うまく素因数分解しましょう。