座標圧縮の解説（1次元から2次元の圧縮まで）
座標圧縮は、座標の情報から、位置関係や大小関係だけ抽出するテクニックです。
仮に座標の範囲が非常に広い場合、以下のような不都合が生じてしまいます。
- 例：\(0\) ~ \(10^9\) の数直線はメモリにのらない
- 例：\(10^9 \times 10^9\) の領域はメモリにのらない
このような状況では、情報を圧縮しなければ探索などを行うことができません。
情報のない空白部分が連続している場合、不要部分として削除してやることで圧縮することができます。
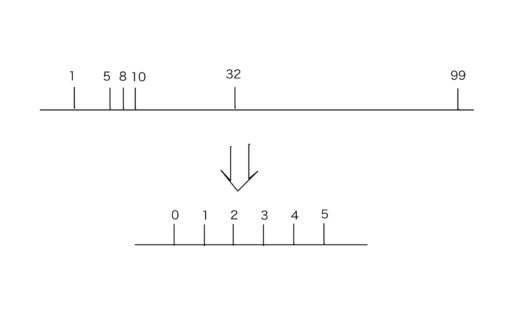
また、必要な情報を残しておけば、圧縮前の位置を復元してやることも可能です。
一次元のとき
以下のように、与えられた数列から、大小関係だけを抽出したい場合を考えます。
入力: 1 10 5 32 99 8 10
出力: 0 3 1 4 5 2 3
※上の例のように同じ値には同じ番号をつける
※大小関係は「左から何番目か」と言い換えることもできます。この考え方は二次元になった時も有効です。
アルゴリズム
数列 X の座標圧縮
- 数列 X をソートした結果を vals とする
- vals の重複した値を削除する
- X のそれぞれの要素について、vals の中の何番目に出現するかを二分探索などで調べる
※具体例として、X を「1 10 5 32 99 8 10」として考えてみましょう。
- 数列 X をソートした結果を vals : 「1 5 8 10 10 32 99」
- vals の重複した値を削除 : 「1 5 8 10 32 99」
- X のそれぞれの要素について、vals の中の何番目に出現するかを二分探索などで調べる
- X[0] (1) : 0番目
- X[1] (10) : 3番目
- X[2] (5) : 1番目
- X[3] (32) : 4番目
- X[4] (99) : 5番目
- X[5] (8) : 2番目
- X[6] (10) : 3番目
以上より、結果は「0 3 1 4 5 2 3」になります。
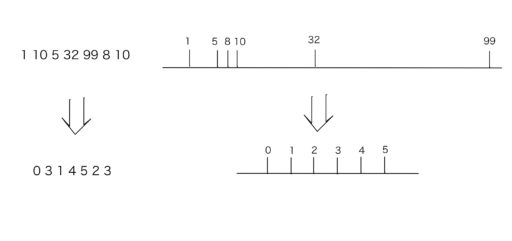
※vals の結果（上の例では「1 5 8 10 32 99」）を残しておけば、圧縮後の X から元々の X を復元することが可能です。
計算量
- \(O(N \log N)\)
数列 X の要素数を \(N\) とすると、ソートに \(O(N \log N)\) かかります。また、\(O(\log N)\) の二分探索を \(N\) 回行うことになるので、全体では \(O(N \log N)\) となります。
C++ での実装例
数列 X を受け取り、圧縮した結果に書き換える関数の例です。
返り値としては、元々の X の値をソートして重複を削除したもの(vals)を返すようにしています。このようにする理由としては、座標圧縮した結果を元に戻したいときに、vals の値が必要になるからです。
#include <bits/stdc++.h>
using namespace std;
/* compress
X を座標圧縮して書き換える（副作用）
返り値: ソート済みの値
計算量: O(n log n)
*/
template <typename T>
vector<T> compress(vector<T> &X) {
// ソートした結果を vals に
vector<T> vals = X;
sort(vals.begin(), vals.end());
// 隣り合う重複を削除(unique), 末端のゴミを削除(erase)
vals.erase(unique(vals.begin(), vals.end()), vals.end());
// 各要素ごとに二分探索で位置を求める
for (int i = 0; i < (int)X.size(); i++) {
X[i] = lower_bound(vals.begin(), vals.end(), X[i]) - vals.begin();
}
return vals;
}
二次元のとき
多くの場合は、以下のような状況で座標圧縮を行います。
- 長方形が与えられる（左上と右下の頂点の座標が渡される）
- 縦線と横線が与えられる（端点の座標が渡される）
- 点(1マス)が与えられる
これらの情報を座標圧縮してやることで、二次元配列上で様々なアルゴリズムを適用することが可能になります。
以下は座標圧縮前と後の図です。この例ではあまり圧縮されていないように感じるかもしれませんが、線分同士の間隔が非常に広い場合にはとても強力な道具になります。
. . . . . . . # . . # # # # . . . # . . . . . . . . . # . . . . . . . . . # . . . . . # . . . # . . . # # # # # # # # . . . . # . . . # . . . . . # . . . # . . . . . # . . . # . . . . . # . . . . . .
. . . . . # . # # # # . # . . . . . . . # . . . . . # . # . . . # # # # # # . . . . # . # . . . . . # . # . . . . . # . . . .
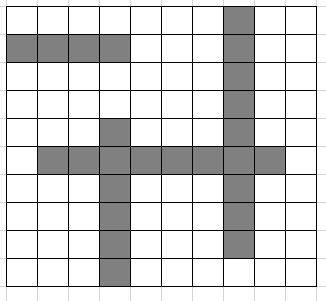
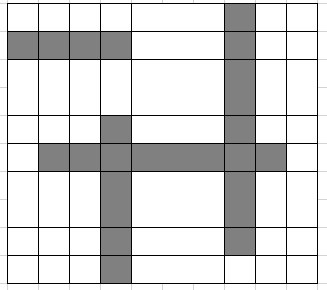
アルゴリズム
今回は、線の端点 (X1, Y1),(X2, Y2) が以下のように N 個与えられる時の座標圧縮を考えてみます。
N
X1[0] Y1[0] X2[0] Y2[0]
X1[1] Y1[1] X2[1] Y2[1]
…
X1[N-1] Y1[N-1] X2[N-1] Y2[N-1]
基本は１次元の時と同じです。X方向とY方向に分けて考えましょう。
二次元での座標圧縮：
- X1,X2 と Y1,Y2 で分けて、一次元での座標圧縮を行う(以下 X1,X2 について考える)
- X1,X2 の要素と、その一つ隣の要素を全てまとめて、ソートした結果を vals とする
- vals の重複した値を削除する
- X1,X2 のそれぞれの要素について、vals の中の何番目に出現するかを二分探索などで調べる
※一つ隣の要素も確保しないと空白が埋まることがあります（後述）
※以下の入力例での座標圧縮を見てみましょう（前述の図で示した例と同じ設定です）
4
1 0 1 3
5 1 5 8
4 3 9 3
0 7 8 7
X1 は 「1 5 4 0」であり、X2 は「1 5 9 8」です。それぞれの一つ隣の要素（つまり＋１した値）も vals に含めるので、vals の値はソートして重複を削除すると「0 1 2 4 5 6 8 9 10」になります。
よって、X1, X2 の座標圧縮後の値は、X1 は「1, 4, 3, 0」で X2 は「1,4,7,6」です。
以下の図と対応していることを確認してみてください。（縦方向をX軸としています。）
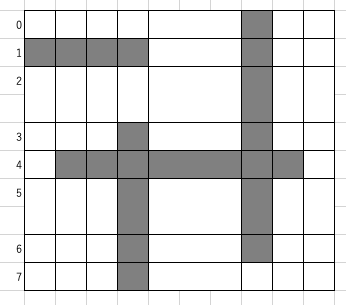
二次元での座標圧縮での注意点
前述の通り、一つ隣の要素も含めてやらないと、必要な空白部分がなくなってしまう可能性があります。つまり、空白でできた領域がなくなってしまう場合があるのです。
圧縮前
. . . . . . . # . . # # # # . . . # . . . . . . . . . # . . . . . . . . . # . . . . . # . . . # . . . # # # # # # # # . . . . # . . . # . . . . . # . . . # . . . . . # . . . # . . . . . # . . . . . .
正しい圧縮（一つ隣も含める）
. . . . . # . # # # # . # . . . . . . . # . . . . . # . # . . . # # # # # # . . . . # . # . . . . . # . # . . . . . # . . . .
失敗した圧縮（隣を含めない）
. . . # . # # # # . . . # # . . # # # # . . # # . . . # . .
座標圧縮で必要な部分を示すと以下のようになります。
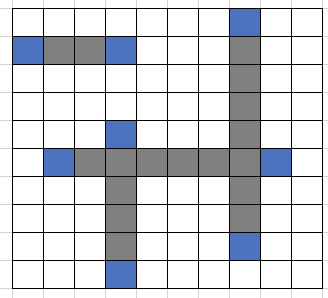
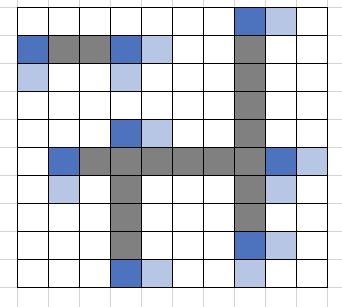
この例では、一つ隣（右側と下側）部分の余白のみを確保しました。例えば、「線分で囲まれた部分の領域があるか」考えるような問題では、右側の余白だけで十分です。
左側も余白として確保しないと、左端の余白が消失してしまう可能性があります。この部分を余白として確保するかどうかは、問題や実装によって変わってくるでしょう。
基本的には、必要にならない限り余分な余白は確保しない方が良いでしょう。座標圧縮後のサイズが増えてしまうので、入力によっては配列が確保しきれなかったりするなどの問題が発生してしまうからです。
計算量
- \(O(N \log N)\)
与えられた座標の要素数を \(N\) とすると、一次元とほぼ同じ内容をそれぞれの方向について行うだけなので、計算量は大きく変わりません。
むしろ、2次元での座標圧縮の場合は、座標圧縮後の操作がボトルネックになることが多いでしょう。
C++ での実装例
/* compress
(X1,Y1),(X2,Y2)という二点で表されるもの（長方形や直線など）について、行か列の片方（X1とX2 or Y1とY2）を座標圧縮する（副作用）
返り値: ソートされ重複要素を除いた値
計算量: O(n log n)
*/
template <typename T>
vector<T> compress(vector<T> &C1, vector<T> &C2) {
vector<T> vals;
int N = (int)C1.size();
for (int i = 0; i < N; i++) {
for (T d = 0; d < 1; d++) { // その位置と、一つ隣を確保(隣を確保しないと空白が埋まってしまうことがある)
T tc1 = C1[i] + d;
T tc2 = C2[i] + d;
vals.push_back(tc1);
vals.push_back(tc2);
}
}
// ソート
sort(vals.begin(), vals.end());
// 隣り合う重複を削除(unique), 末端のゴミを削除(erase)
vals.erase(unique(vals.begin(), vals.end()), vals.end());
for (int i = 0; i < N; i++) {
C1[i] = lower_bound(vals.begin(), vals.end(), C1[i]) - vals.begin();
C2[i] = lower_bound(vals.begin(), vals.end(), C2[i]) - vals.begin();
}
return vals;
}
問題例：AOJ DSL_4_A – Union of Rectangles
問題例を通して、実際の使い方を学びましょう。
問題概要
平面上に N 個の長方形があります。１つ以上の長方形で覆われている部分の面積を求めてください。
制約
- \(1 \leq N \leq 2000\)
- 長方形は左上と右下の座標が与えられ、 \(- 10^9\) ~ \(10^9\) の範囲の整数
考え方
座標の範囲がメモリにのるくらい小さければ、全てのマスを探索して長方形で覆われているマスを一つずつ数えれば良いです。
しかし、\(- 10^9\) ~ \(10^9\) の範囲となっているので、そのままでは全てを探索することはできません。座標圧縮をして、二次元配列として表せるようにしましょう。
座標圧縮後の手順としては、
- 長方形で覆われているマスをマークする
- マークされたマスの(圧縮される前の)面積を全て足し合わせる
とすれば良いです。圧縮前の面積は、圧縮前の座標を確認してやることで簡単に復元することが可能です。
補足：この問題設定では、実は一つ隣を確保しなくても解くことができます。問題文の入力として与えられるのは、長方形の左上と右下の座標です。
座標をマスに1対1に対応させると、左上の座標は長方形の上にあるマスに対応し、右下の座標は長方形の外にあるマス（つまり余白部分）に対応させることができます。
よって、一つ隣を確保しなくても、うまく空白を保って座標圧縮を行うことができます。
解法
- 座標圧縮する
- 2次元での imos 法などを用いて、長方形が重なる部分をマークする
- マークされたマスの(圧縮される前の)面積を全て足し合わせる
C++ での実装例
/* coordinate_compress_2D.cpp
2Dの座標圧縮を行う
verified: [AOJ] DSL_4_A Union of Rectangles
http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=DSL_4_A&lang=ja
*/
#include <bits/stdc++.h>
using namespace std;
/* compress
(X1,Y1),(X2,Y2)という二点で表されるもの（長方形や直線など）について、行か列の片方（X1とX2 or Y1とY2）を座標圧縮する（副作用）
返り値: ソートされ重複要素を除いた値
計算量: O(n log n)
*/
template <typename T>
vector<T> compress(vector<T> &C1, vector<T> &C2) {
vector<T> vals;
int N = (int)C1.size();
for (int i = 0; i < N; i++) {
for (T d = 0; d <= 1; d++) { // for (T d = 0; d <= 0; d++) でも良い
T tc1 = C1[i] + d;
T tc2 = C2[i] + d;
vals.push_back(tc1);
vals.push_back(tc2);
}
}
// ソート
sort(vals.begin(), vals.end());
// 隣り合う重複を削除(unique), 末端のゴミを削除(erase)
vals.erase(unique(vals.begin(), vals.end()), vals.end());
for (int i = 0; i < N; i++) {
C1[i] = lower_bound(vals.begin(), vals.end(), C1[i]) - vals.begin();
C2[i] = lower_bound(vals.begin(), vals.end(), C2[i]) - vals.begin();
}
return vals;
}
int main() {
// 入力
int N;
cin >> N;
vector<long long> X1(N), Y1(N), X2(N), Y2(N);
for (int i = 0; i < N; i++) {
cin >> X1.at(i) >> Y1.at(i) >> X2.at(i) >> Y2.at(i);
}
// 座標圧縮
vector<long long> X = compress(X1, X2);
vector<long long> Y = compress(Y1, Y2);
// imos法で塗りつぶし
int w = (int)X.size();
int h = (int)Y.size();
vector<vector<int>> G(w, vector<int>(h));
for (int i = 0; i < N; i++) {
G[X1[i]][Y1[i]]++;
G[X2[i]][Y2[i]]++;
G[X1[i]][Y2[i]]--;
G[X2[i]][Y1[i]]--;
}
for (int x = 1; x < w; x++) {
for (int y = 0; y < h; y++) {
G[x][y] += G[x - 1][y];
}
}
for (int x = 0; x < w; x++) {
for (int y = 1; y < h; y++) {
G[x][y] += G[x][y - 1];
}
}
// 塗りつぶしたマスの面積を全て足し合わせる
long long ans = 0;
for (int x = 0; x < w - 1; x++) {
for (int y = 0; y < h - 1; y++) {
if (G[x][y]) {
ans += (X[x + 1] - X[x]) * (Y[y + 1] - Y[y]);
}
}
}
cout << ans << endl;
}
練習問題
座標圧縮はイメージしにくいと思います。練習問題を解きながら感覚を掴んでください。
一次元
- AtCoder Beginner Contest 036 C – 座圧 : 1次元の座標圧縮そのものです
- AtCoder Beginner Contest 113 C – ID：県ごとに座標圧縮
二次元
- AOJ DSL_4_A – Union of Rectangles
- JOI 2007/2008 本選 問題5 E – ペンキの色：領域の数を数えます
- 第１２回日本情報オリンピック 予選（オンライン）E – 魚の生息範囲 (Fish)：3次元の座標圧縮ですが、基本は2次元と同じです
- AtCoder Beginner Contest 168 F – . (Single Dot)：難しいです。線分の座標圧縮をします。幅がないので幅0のマスとして見てやると扱いやすいです。実装上は、そのまま座標圧縮したあとに二次元配列を縦横2倍に拡大してやり、偶数番目を幅0と扱うのが楽でしょう。隣のマスを確保して座標圧縮する必要がなくなります。むしろとなりのマスまで含めると、配列のサイズが膨れ上がってしまうので TLE になるかもしれません。