幅優先探索(Breadth First Search)の基本
幅優先探索とは、全探索アルゴリズムの一種です。最短経路を求める際に使用される基本的なアルゴリズムです。
木などのグラフやグラフと同一視できるものを探索する際に良く使われます。深さ優先探索と似ていますが、幅優先探索は始めの状態に近いものから順番に探索していきます。
英語では Breadth First Search なので、BFSと略されることも多いです。
以下のような順番で探索していきます。
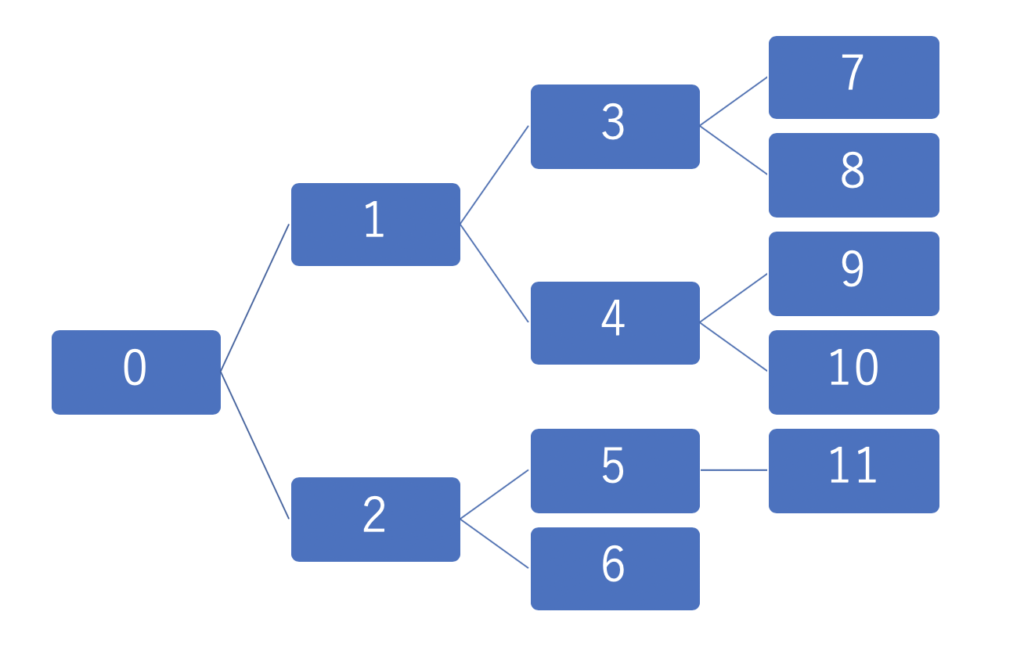
アルゴリズム
幅優先探索ではキューを用いることで以下のように探索することができます。
キューを用いたアルゴリズム：
- 始めの状態から遷移可能な状態を、全てキューに入れる
- キューに要素がなければ終了する
- 現在の状態から遷移可能な状態を、全てキューに入れる
- キューから1つ要素を取り出し、そこに状態を遷移させる
- 2.に戻る
※ キューではなくスタックで実装すると、深さ優先探索になります。
※ 途中まで探索した時は以下のような状態になります。状態を変更するたびに、キューに遷移可能な場所の情報を入れましょう。
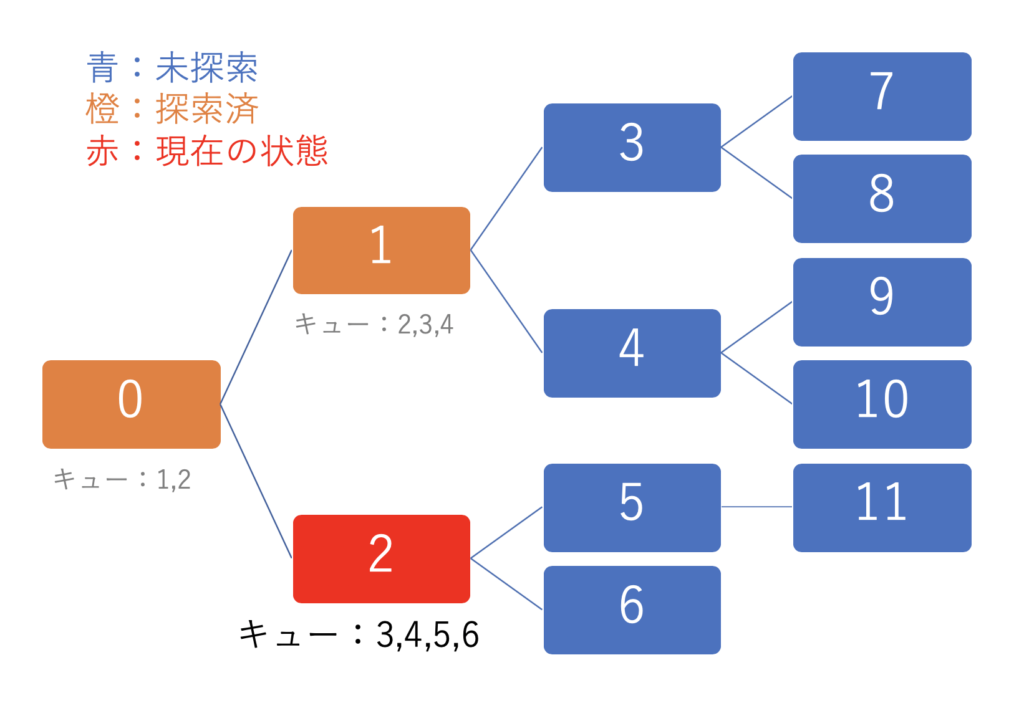
※既に行ったことのある場所(上の図では0など)をキューに入れるようにすると無限ループになってしまうので気をつけましょう。
計算量
- O(V+E)
グラフ \(G=(V,E)\) を幅優先探索する場合は、（状況にもよりますが）全ての頂点と辺を走査することになるので、計算量は O(V+E) になります。
問題1：BFSで同じ連結成分に属するか判定（グラフ）
頂点数 V 、辺の数 E のグラフについて、頂点 s から頂点 t に到達できるかを探索するプログラムを書いてみましょう。到達できれば 'yes’ と出力し、到達できなければ 'no’ と出力します。
入力形式
V, E, s, t に加えて、ai から bi への有向辺が E 個与えられます。
V E
s t
a1 b1
a2 b2
…
aE bE
入出力例
入力：
4 5
0 3
0 1
0 2
1 3
2 1
2 3
出力：
yes
この例では以下のようなグラフになります。
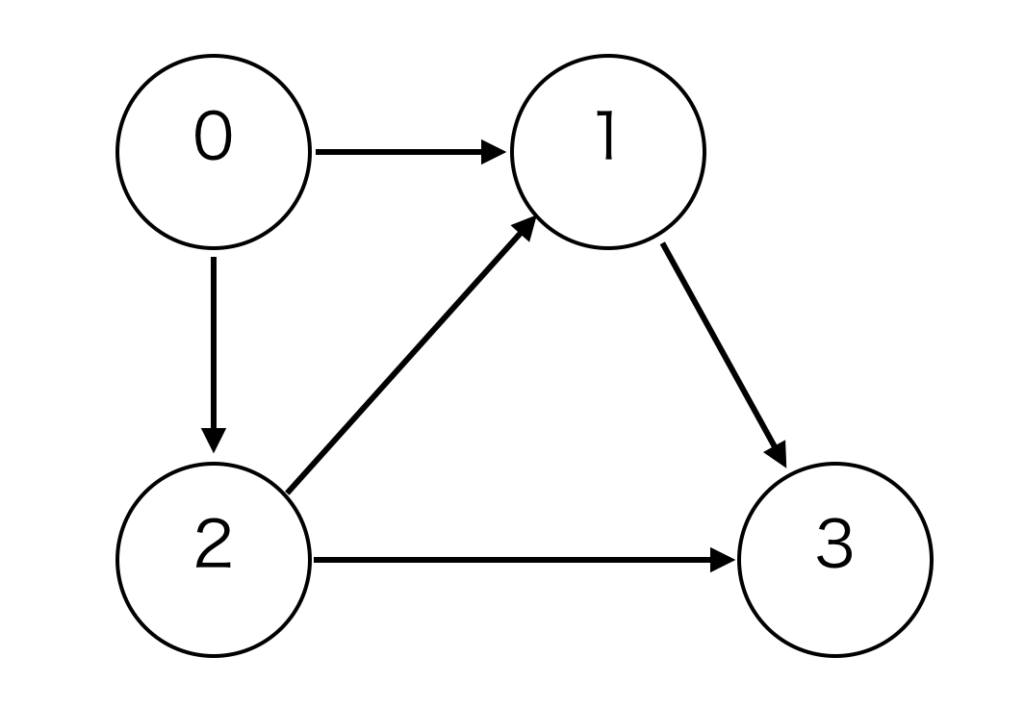
0からスタートして、3にたどり着ければ 「yes」、たどり着けなければ「no」を返します。この場合はたどり着けるので yes となります。
隣接行列・隣接リスト(グラフを参照)のどちらでグラフを表現するのか、スタック・再帰関数のどちらで深さ優先探索を実装するのかで、やり方が色々と変わってきます。
C++の実装例
隣接リスト表現(グラフを参照のこと)を用いると以下のようになります。
#include <bits/stdc++.h>
using namespace std;
int main() {
int V, E;
cin >> V >> E;
int s, t;
cin >> s >> t;
vector<vector<int>> G(V);
for (int i = 0; i < E; i++) {
int a, b;
cin >> a >> b;
G[a].push_back({b});
// G[b].push_back({a});
}
vector<bool> seen(V, false); // 既に見たことがある頂点か記録する
queue<int> que;
que.emplace(s); // sから探索する
seen[s] = true;
while (que.size() != 0) { // 幅優先探索
int state = que.front(); // 現在の状態
que.pop();
for (auto next : G[state]) {
if (!seen[next]) { // 未探索の時のみ行う
seen[next] = true;
que.emplace(next); //次の状態をqueueへ格納
}
}
}
if (seen[t]) {
cout << "yes" << endl;
} else {
cout << "no" << endl;
}
return 0;
}
問題2：BFSで重みなし最短経路問題（グリッドグラフ）
幅優先探索は、重みなしグラフの単一始点最短経路を求める際にも利用されます。AtCoder ABC007 C – 幅優先探索 を解いてみましょう。
問題概要
R行C列の迷路が与えられる。スタートの ( sy, sx ) からゴールの ( gy, gx ) までの最短距離を求めよ。
考え方
スタート地点から、幅優先探索によりゴールまでの最短距離を求めれば完了です。通った点について、スタート地点からの最短距離を記録していきましょう。
迷路上での探索なので、先程のグラフの例と少し実装が異なりますが、基本となるアルゴリズムは変わりません。
C++ での実装例
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int INF = 2100100100;
int R, C;
vector<vector<char>> maze; // 迷路の内容を保存する配列
vector<vector<int>> dist; // 距離を記録しておく配列
int sx, sy, gx, gy;
int main() {
cin >> R >> C;
cin >> sy >> sx;
cin >> gy >> gx;
sy--; // 0始まりに直す
sx--;
gy--;
gx--;
dist.assign(R, vector<int>(C, INF)); // 初期化
maze.assign(R, vector<char>(C, '.')); // 初期化
for (int i = 0; i < R; i++) {
for (int j = 0; j < C; j++) cin >> maze[i][j];
}
queue<pair<int, int>> que;
que.emplace(make_pair(sy, sx)); // sから探索する
dist[sy][sx] = 0;
while (que.size() != 0) { // キューの要素がなくなったら終了
pair<int, int> now = que.front(); // 現在の状態
que.pop();
if (now.first == gy && now.second == gx) { // 目的地にたどり着いたので終了
break;
}
int dy[4] = {0, 0, 1, -1}; // dx,dy は次の探索場所への距離を表す（４方向分）
int dx[4] = {1, -1, 0, 0};
for (int i = 0; i < 4; i++) {
int ny = now.first + dy[i]; // 次の探索場所の行番号
int nx = now.second + dx[i]; // 次の探索場所の列番号
if (ny < 0 || R <= ny || nx < 0 || C <= nx) continue; // 迷路の外に出るならスルー
if (maze[ny][nx] == '#') continue; // 障害物があればスルー
if (dist[ny][nx] != INF) continue; //探索済みならスルー
que.push(make_pair(ny, nx));
dist[ny][nx] = dist[now.first][now.second] + 1;
}
}
cout << dist[gy][gx] << endl;
return 0;
}