二次元での区間和を求めるアルゴリズム(区間の更新なし)
大きさが \(H × W\) の二次元配列 \(a\) 上において、 [h1,h2)×[w1,w2) の範囲の区間和を求めるアルゴリズムについてです。
input:
a = {{1, 2, 3, 4},
{1, 2, 3, 4},
{1, 2, 3, 4},
{1, 2, 3, 4}}
[h1,h2)×[w1,w2) = [1,3)×[2,3)
output:
6
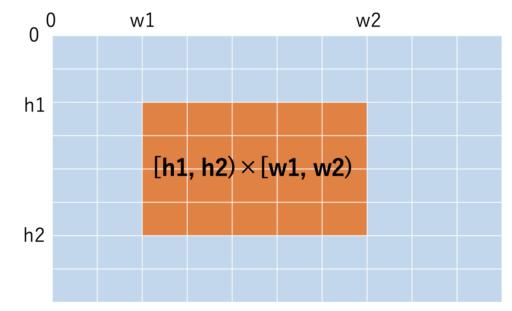
行列 \(a\) に対して、[h1,h2)×[w1,w2)の範囲の部分行列の要素の合計値を求める問題とも言えます。
アルゴリズム
単純なアルゴリズム(前処理なし):
- 以下を計算する
a[h1][w1] + a[h1][w1+1] + … + a[h1][w2-1]
+ a[h1+1][w1] + a[h1+1][w1+1] + … + a[h1+1][w2-1]
+ …
+ a[h2-1][w1] + a[h2-1][w1+1] + … + a[h2-1][w2-1]
効率的なアルゴリズム(前処理あり):
- 前処理
- 累積和「S[h][w] = [0, h)×[0, w) の区間の和」 を計算しておく
- クエリ( [h1,h2)×[w1,w2) の範囲の区間和 を求める)
- S[h2][w2] – S[h1][w2] – S[h2][w1] + S[h1][w1] を計算する
※ 前処理では「S[h][w] = a[h-1][w-1] + S[h][w-1] + S[h-1][w] – S[h-1][w-1] 」とすると高速に計算ができます。
※ クエリでの「S[h2][w2] – S[h1][w2] – S[h2][w1] + S[h1][w1]」は求める値に一致します。
計算量
- 単純なアルゴリズム
- 前処理:なし
- クエリ:\(O(HW)\)
- 効率的なアルゴリズム(前処理あり)
- 前処理:\(O(HW)\)
- クエリ:\(O(1)\)
C++ での実装例(効率的なアルゴリズム)
#include <bits/stdc++.h>
using namespace std;
// 前処理を行う
void pre_process(vector<vector<int>> const &a, vector<vector<int>> &S) {
int H = (int)a.size();
int W = (int)a[0].size();
S.assign(H + 1, vector<int>(W + 1));
for (int h = 1; h < H + 1; h++) {
for (int w = 1; w < W + 1; w++) {
S[h][w] = a[h - 1][w - 1] + S[h][w - 1] + S[h - 1][w] - S[h - 1][w - 1];
}
}
}
// [h1,h2)×[w1,w2) の区間和を求める
int query(int h1, int h2, int w1, int w2, vector<vector<int>> const &S) {
return S[h2][w2] - S[h1][w2] - S[h2][w1] + S[h1][w1];
}
int main() {
vector<vector<int>> a = {{1, 2, 3, 4},
{1, 2, 3, 4},
{1, 2, 3, 4},
{1, 2, 3, 4}};
vector<vector<int>> S;
pre_process(a, S);
cout << query(1, 3, 2, 3, S) << endl; // [1,3)×[2,3) = 3+3 = 6
cout << query(0, 4, 0, 4, S) << endl; // [0,4)×[0,4) = 40
return 0;
}
二次元累積和の気持ち
前処理(累積和の計算)
以下のような累積和 S[h][w] を前処理 \(O(HW)\) で求めることを考えます。
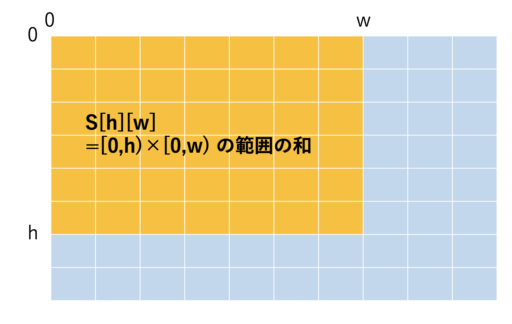
以下の 3 つを足しわせて、重複部分を引けば累積和を求めることができます。
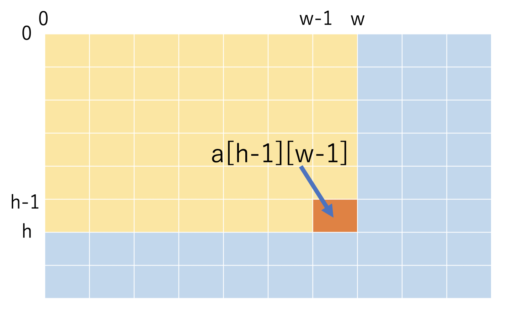

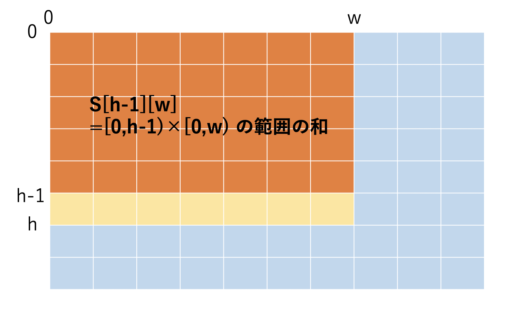
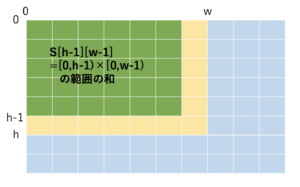
数式で表すと以下の通りです。
- S[h][w] = a[h-1][w-1] + S[h][w-1] + S[h-1][w] – S[h-1][w-1]
これにより、前の計算結果を利用することで次の累積和を計算できるようになりました。
コードでは以下のようになります。
void pre_process(vector<vector<int>> const &a, vector<vector<int>> &S) {
int H = (int)a.size();
int W = (int)a[0].size();
S.assign(H + 1, vector<int>(W + 1));
for (int h = 1; h < H + 1; h++) {
for (int w = 1; w < W + 1; w++) {
S[h][w] = a[h - 1][w - 1] + S[h][w - 1] + S[h - 1][w] - S[h - 1][w - 1];
}
}
}
この前処理にかかる計算量は \(O(HW)\) です。
区間和の取得
前処理して求めた累積和を利用して、任意の長方形の区間の和を求めることができます。
以下のように [h1,h2)×[w1,w2) の範囲の区間和を求めることを考えてみましょう。

累積和を求めた時と似たような方法で、4つを組み合わせると簡単に求めることができます。
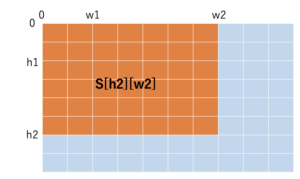
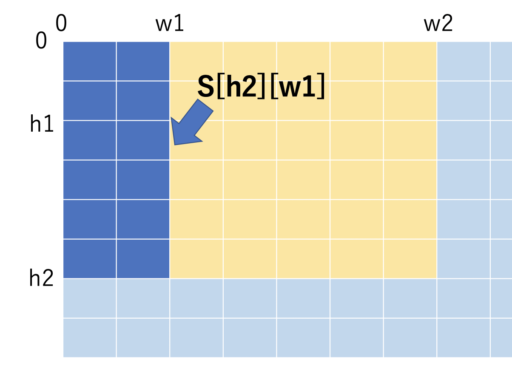
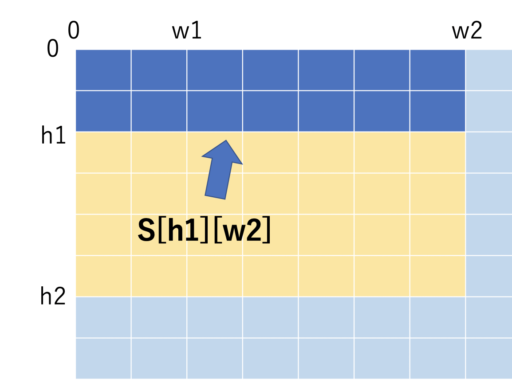
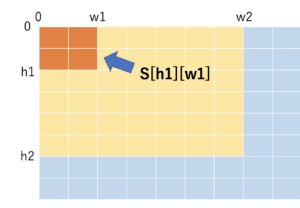
数式で表すと以下のようになります。
- [h1,h2)×[w1,w2) の範囲の区間和 = S[h2][w2] – S[h1][w2] – S[h2][w1] + S[h1][w1]
累積和は既に前処理で計算してあるので、このクエリに必要な計算量は \(O(1)\) になります。
コードでは以下の通りです。
// [h1,h2)×[w1,w2) の区間和を求める
int query(int h1, int h2, int w1, int w2, vector<vector<int>> const &S) {
return S[h2][w2] - S[h1][w2] - S[h2][w1] + S[h1][w1];
}
参考
区間の更新がある場合
値を途中で変更するなどの「更新」があった場合は、累積和を計算し直す必要があるので逆に非効率になります。
そのような場合は、BIT などのデータ構造を2次元に対応させると
- 更新:\(O(\log HW)\)
- クエリ:\(O(\log HW)\)
で処理ができます。
ディスカッション
コメント一覧
まだ、コメントがありません