Union-Find Tree を理解する！素集合系を扱うデータ構造

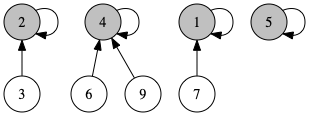
2020年1月18日データ構造競プロ,データ構造,連結成分,Union-Find

2つの集合が共通する要素を持たない時に「互いに素」であると言い、このような集合の集まりを「素集合系」などと言います。

素集合系
素集合系の例

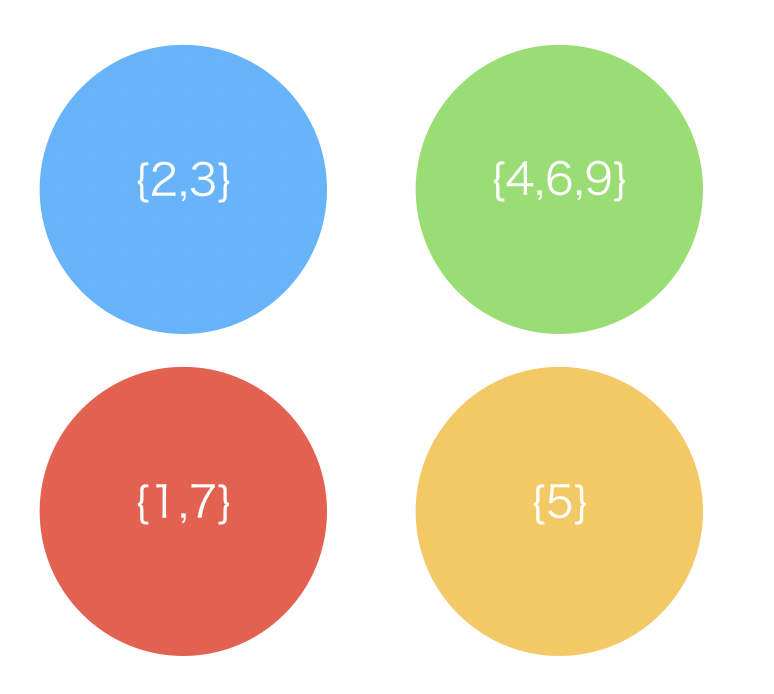
素集合系は、いくつかの木構造を用いることで管理することができます。1つの集合は1つの木を用いて表現され、各ノードが集合に含まれる元になります。

このような木を Union-find Tree と言います。

Union-find Tree
素集合系の例の時のUnion-find Tree

工夫をすれば、集合に新たな要素を加えるor集合同士をまとめる操作や、同じ集合に要素があるかを判定する操作を\(O(logn)\)よりも高速に行うことができます。

Union-find Tree

Union-find Tree はデータを互いに素な集合(素集合系)にして管理するためのデータ構造です。主に以下の操作が行えます。

  • makeTree(x) : 新しく x を根とした木をつくる
  • findRoot(x) : xを含む木の根（root）を求める。木の根を代表点（representative）と言ったりする。
  • union(x,y) : 指定された2つ要素 x,y を含む木を併合する
  • isSame(x,y) : x,y が同じ木（集合）にあるのかを、根が同じかで判定する

1つの木が、1つの集合を表しています。工夫をすれば、木(集合)同士の併合や、同じ集合に含まれているかの判定は高速にできます。

しかし、一度まとめた集合を分割したり、ノードを削除したりするのにはあまり向いていません。

まずは、なにも工夫しない場合における操作を詳しく見ておきましょう。

makeTree(a)

makeTree(x) によって、新しく a を根とした木をつくることができます。例えば、makeTree(2)では以下のようになります。

makeTree(2)によってできる木
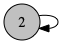
void makeSet(int x) {
    parents[x] = x; // parents[i]:=iの親
}

findRoot(x)

findRoot(x)によって、xを含む木の根、つまり代表となる点を求めます。例えば、以下のような木に対してfindRoot(6)を行った場合は、代表点である4を返します。

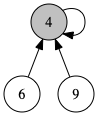
int findRoot(int x) {
    if (x == parent[x])
        return x;
    return findRoot(parent[x]);
}

union(x,y)

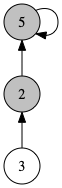
2つの木をつなげることを考えましょう。以下の図の時を例に考えます。

union(3,5) によって、3を含む木と5を含む木を1つにまとめます。出来上がる木の代表点は、もともとの木の2つの代表点のどちらかになるようにしましょう。

void unite(int x, int y) {
    x = findRoot(x);
    y = findRoot(y);
    if (x != y)
        parents[x] = y;
}

高速化の工夫

先程の実装のように、普通に木を作って何も考えずに併合することを繰り返すと、以下のように木が長くなってしまう可能性があります。

木の高さが頂点数と同じ例
木の高さが頂点数と同じ例

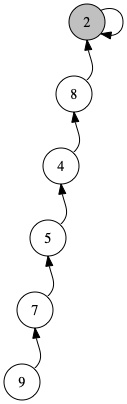
こうなると、例えば findRoot(9) などを行うとき、木の下から順番に全てのノードをたどる必要があるので、頂点数 n に応じた時間がかかってしまい効率が悪くなります。

これを防ぐためには、主に2種類の手法を組み合わせて使います。

  • 経路圧縮：findRoot(x)の際にたどった頂点は、全て木の根に直接繋がるようにする
  • 高さ/サイズ による合併：union(x,y) の際には、木の高さの低い物（木のサイズが小さい物）を、高い方の木の根(root)に直接つける

どちらか片方だけでも、findRoot(x) や isSame(x,y) の計算量が\(O(logn)\)まで高速化できます。

経路圧縮

左図のような木について、findRoot(9)をすることを考えます。下から代表点である2へとたどるついでに、途中の点を全て2へと繋いでしまえば、右図のように木の高さが低くなります。

もとの木
経路圧縮後の木

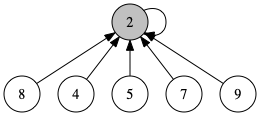
先程の findRoot(x)を変更して、自身の親を、木の根に更新するコードにしましょう。

int findRoot(int x) {
    if (x != parents[x]) {
        parents[x] = findRoot(parents[x]); 
    }
    return parents[x];
}

この工夫により、計算量が\(O(n)\)から\(O(logn)\)になります。

高さ/サイズ による合併

以下の例において、union(2,5) によって、2を含む木と5を含む木を1つにまとめることを考えましょう。

この時、代表点2の木と代表点5の木のどちらをどちらに繋げるのかで効率が変わってきます。戦略としては主に2種類あって、

  • 木の高さが低い方を高い方へ繋げる
  • 木のサイズ（ノード数）が小さい方を大きい方へ繋げる

どちらの戦略であっても、今回は以下のようになります。

効率的な併合

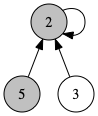
逆のつなげ方をすると、以下のように木の高さが3になってしまい、計算が非効率になってしまいます。

非効率な併合

木の高さによる更新は以下のようにします。

void makeTree(int x) {
    parents[x] = x; // the parent of x is x
    rank[x] = 0;
}
void unite(int x, int y) {
    x = findRoot(x);
    y = findRoot(y);
    if (rank[x] > rank[y]) { // rankは木の高さを表す
        parents[y] = x;
    } else {
        parents[x] = y;
        if (rank[x] == rank[y]) {
            rank[y]++;
        }
    }
}

木のサイズによる更新は以下のようにします。

void makeTree(int x) {
    parents[x] = x; // the parent of x is x
    size[x] = 1;
}
bool unite(int x, int y) {
    x = findRoot(x);
    y = findRoot(y);
    if (x == y) return false;
    if (size[x] > size[y]) {
        parents[y] = x;
        size[x] += size[y];
    } else {
        parents[x] = y;
        size[y] += size[x];
    }
    return true;
}

証明は難しいのでこの記事では詳しく説明しませんが、この工夫により計算量が\(O(n)\)から\(O(logn)\)になります。経路圧縮と合わせると、アッカーマン関数の逆関数\(\alpha\) を用いて、\(O(\alpha(n))\)で計算できることが知られています（\(O(logn)\)よりも高速）。

C++の実装例

union by rank

まずはrankによる併合から。

/* UnionFind：素集合系管理の構造体(union by rank)
    isSame(x, y): x と y が同じ集合にいるか。 計算量はならし O(α(n))
    unite(x, y): x と y を同じ集合にする。計算量はならし O(α(n))
*/
struct UnionFind {  // The range of node number is from 0 to n-1
    //'rank[x]' is a rank of the union find tree the root of which is x.
    //'parents[x]' is the parent of x
    vector<int> rank, parents;
    // constructor
    UnionFind() {}
    UnionFind(int n) {  // make n trees.
        rank.resize(n, 0);
        parents.resize(n, 0);
        for (int i = 0; i < n; i++) {
            makeTree(i);
        }
    }
    // make a union find tree
    void makeTree(int x) {
        parents[x] = x;  // the parent of x is x
        rank[x] = 0;
    }

    // check whether the root of x is the same as that of y
    bool isSame(int x, int y) { return findRoot(x) == findRoot(y); }

    // unite two tree
    bool unite(int x, int y) {
        x = findRoot(x);
        y = findRoot(y);
        if (x == y) return false;
        if (rank[x] > rank[y]) {
            parents[y] = x;
        } else {
            parents[x] = y;
            if (rank[x] == rank[y]) {
                rank[y]++;
            }
        }
        return true;
    }

    // travel the parents of tree recursivily to find root
    int findRoot(int x) {
        if (x != parents[x]) {
            parents[x] = findRoot(parents[x]);  // change the x's parent to the root of tree.
        }
        return parents[x];
    }
};

union by size

サイズによる併合のバージョンです。集合のサイズが分かるという利点があります。

/* UnionFind：素集合系管理の構造体(union by size)
    isSame(x, y): x と y が同じ集合にいるか。 計算量はならし O(α(n))
    unite(x, y): x と y を同じ集合にする。計算量はならし O(α(n))
    treeSize(x): x を含む集合の要素数。
*/
struct UnionFind {
    vector<int> size, parents;
    UnionFind() {}
    UnionFind(int n) {  // make n trees.
        size.resize(n, 0);
        parents.resize(n, 0);
        for (int i = 0; i < n; i++) {
            makeTree(i);
        }
    }
    void makeTree(int x) {
        parents[x] = x;  // the parent of x is x
        size[x] = 1;
    }
    bool isSame(int x, int y) { return findRoot(x) == findRoot(y); }
    bool unite(int x, int y) {
        x = findRoot(x);
        y = findRoot(y);
        if (x == y) return false;
        if (size[x] > size[y]) {
            parents[y] = x;
            size[x] += size[y];
        } else {
            parents[x] = y;
            size[y] += size[x];
        }
        return true;
    }
    int findRoot(int x) {
        if (x != parents[x]) {
            parents[x] = findRoot(parents[x]);
        }
        return parents[x];
    }
    int treeSize(int x) { return size[findRoot(x)]; }
};

※サイズに関しては root に格納された値しか見ないので、親を格納する配列と1つにまとめることもできます。

練習問題

参考

データ構造競プロ,データ構造,連結成分,Union-Find