半分全列挙による全探索の高速化
N 個の要素の組み合わせを計算する際、N/2 ずつの2グループに分けてそれぞれを全列挙し、組み合わせ方を高速に求めるという工夫を「半分全列挙」と言います。
英語では Split and List とか Meet in the middle などと呼ばれることがあるそうです。
簡単な例とアイディアの紹介
正の数からなる要素数 \(N=40\) の数列が与えられ、この中からいくつか選んで合計値を計算します。合計値が S 以下となるような選び方での最大の合計値を求めてみましょう。
N が大きいと全探索できない
単純な全探索では間に合わない
普通に全探索しようとすると、それぞれ「選択する」と「選択しない」の2通りあるので、\(O(2^N)\) の計算量で全ての組み合わせを列挙することができます。
しかし、 \(N=40\) の場合は、\(2^{40} ≒ 10^{12}\) 程度の組み合わせがあるので現実的ではありません。
半分なら全列挙しても間に合う
仮に \(N\) が 20 だった場合は、\(2^{20} ≒ 10^{6}\) 程度の組み合わせなので十分間に合います。
ここが半分全列挙を利用する際の重要なポイントです。
半分ずつに分けて高速化する
N/2 ずつの 2 グループに分けて全列挙
半分なら全列挙しても間に合うので、\(N/2 =20\) ずつの 2 グループに分けることを考えます。
グループの中からいくつか選択して合計値を計算することを考えます。2つのグループがあるので、\(2^{20} ≒ 10^{6}\) 通りの組み合わせが 2 つできることになります。
この組み合わせの集合を \(A, B\) などとします。(要素数は \(10^6\) 程度です。)
2グループ同士を組み合わせる際に高速化
普通に \(A\) と \(B\) を組み合わせて合計値を計算しようとすると、 \(10^6 × 10^6 = 10^{12}\) となってやはり間に合いません。
しかし、問題の条件は合計値が S 以下となる最大の値を求めることです。
仮に \(A\) の要素 \(a\) を固定すれば、「\(S-a\) 以下の最大の要素を \(B\) から選ぶ」という話に変わり、この値は二分探索で高速に求めることができます。
\(A\) の要素を固定して全探索するのに \(O(2^{N/2})\) だけかかり、二分探索に \(O(\log (2^{N/2}) )\) だけかかるので、最終的な計算量は \(O(2^{N/2} N) \) になります。
具体例
上述の手順を具体例で見ておきましょう。以下のような状況で、合計値が S 以下となるような選び方での最大の合計値を求めます。
- \(N = 8\)
- 数列:\(\{31, 15, 11, 20, 13, 8, 5, 9\}\)
- \(S = 62\)
半分に分けて全列挙
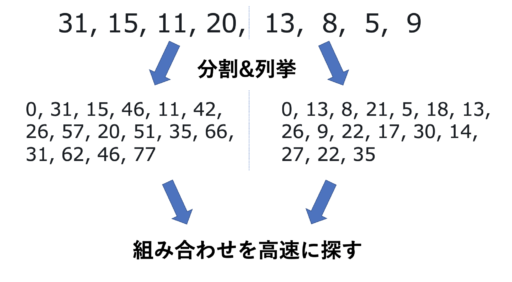
まず数列を以下の2つに分けます。
- グループ1:\(\{31, 15, 11, 20\}\)
- グループ2:\(\{13, 8, 5, 9\}\)
それぞれでの合計値を全列挙すると以下のとおりです。
- A:\(\{0, 31, 15, 46, 11, 42, 26, 57, 20, 51, 35, 66, 31, 62, 46, 77 \}\)
- B:\(\{0, 13, 8, 21, 5, 18, 13, 26, 9, 22, 17, 30, 14, 27, 22, 35 \}\)
片方を固定して二分探索
例えば、A の要素 31 に対して、\(S-31 = 31\) 以下の数の最大値を B の中から探すことを考えてみます。B をソートしておけば二分探索が利用できそうです。
- B:\(\{0, 5, 8, 9, 13, 13, 14, 17, 18, 21, 22, 22, 26, 27, 30, 35\}\)
条件を満たす数に 30 がありました。よってこの時の最大値は 61 になります。
あとは全ての A の要素に対して同様のことを行い、最大値を探せば良いです。ここでは、A の要素に 62 、 B の要素に 0 があるので、最終的な答えは 62 になります。
C++ での実装例
二分探索で「\(S-a\) 以下の最大の要素を \(B\) から選ぶ」場合は、upper_bound(B.begin(), B.end(), S - a) - 1 で選ぶことができます。
しかし、\(S-a\) の値が B の最小の要素よりも小さい場合は、B.begin()-1 と同じになり危ないです。B には必ず 0 が含まれていることに注意して、\(S-a \geq 0\) かをチェックしておきましょう。
また、そもそも \(S-a \geq 0\) が成立しなければ、問題の条件が成立することもありません。
グループごとの全探索は、ビット全探索を用いています。
※ verify していないのでコードが間違っている可能性があります。
#include <bits/stdc++.h>
using namespace std;
int main() {
// 入力
int N, S;
cin >> N >> S;
vector<int> num(N);
for (int i = 0; i < N; i++) {
cin >> num.at(i);
}
// グループ1をビット全探索で全列挙 (前半の半分)
vector<int> A;
for (int bit = 0; bit < (1 << N / 2); bit++) {
int sum = 0;
for (int i = 0; i < (N / 2); i++) {
int mask = 1 << i;
if (bit & mask) {
sum += num[i];
}
}
A.push_back(sum);
}
// グループ2をビット全探索で全列挙 (後半の半分)
vector<int> B;
for (int bit = 0; bit < (1 << (N - N / 2)); bit++) {
int sum = 0;
for (int i = 0; i < (N - N / 2); i++) {
int mask = 1 << i;
if (bit & mask) {
sum += num[N / 2 + i];
}
}
B.push_back(sum);
}
sort(B.begin(), B.end()); // B をソート
// A の要素を固定して二分探索
int ans = 0;
for (auto a : A) {
if (S - a >= 0) {
ans = max(ans, a + *(upper_bound(B.begin(), B.end(), S - a) - 1));
}
}
cout << ans << endl;
return 0;
}
一般化とまとめ
最終的に、半分全列挙のテクニックは以下の形になることが多いです。
- 半分のグループ A を全列挙
- もう半分のグループ B を全列挙
- Aの全ての要素について以下を行う
- A から選ぶ要素を1つに固定したとき、条件に合う要素をBから高速に探す
競技プログラミングで注意しておくポイントとしては、
- 1グループあたり\(10^6 ≒ 2^{20}\) 前後の要素数であることが多い
- 「3.」では 二分探索や map, set など利用して高速化することが多い
などがあるでしょう。
ディスカッション
コメント一覧
まだ、コメントがありません