クラスカル法による最小全域木を求めるアルゴリズム
無向グラフ \(G=(V,E)\) について、\(G\) の部分グラフ \(T\) が以下を満たす時、\(T\) は全域木(Spanning Tree) と言います。
- \(T\) は木
- \(T\) では\(V\) の任意の2頂点を連結にする(\(T\) は \(G\) の頂点 \(V\) を全て使っている)
特に \(T\) で使われる辺のコストの和が最小であるときは、最小全域木(MST: Minimum Spanning Tree)と呼ばれます。

クラスカル方は最小全域木を求めるアルゴリズムです。同様に最小全域木を求めるアルゴリズムとして、プリム法があります。
アルゴリズム
クラスカル法:
- 辺集合 \(E\) をコストの小さい順にソートする
- 以下を \(V-1\) 個の辺を選ぶまで(最小全域木 \(T\) ができるまで)繰り返す
- 残っている辺の中からコストが最小の辺 e を取り出す。現在構成中の \(T\) に e を加えても閉路ができないなら \(T\) に加える。
※ 辺 e=(u,v) を加えて閉路ができるのは、u と v が連結な時です。この判定は Union-Find Tree を使えば高速にできます。(参考:グラフの2頂点が同じ連結成分に属するか判定するアルゴリズム)
計算量
- \(O(|E| \log |V|)\)
辺をソートするのに一番時間がかかります。これは \(O(|E| log |E|)\) です。\(|E| \leq |V|^2\)と合わせると、\(O(|E| log |V|^2)\)が成り立ちます。
また、\(\log |V|^2 = 2 \log |V|\) から \(O(2 |E| \log |V|)\) になり、オーダー記法では定数倍は無視できるので、これは \(O(|E| \log |V|)\) と同じです。
ただ、ここまでの式変形を考えなくても、\(O(|E| \log |E|)\) で実用上は問題ないと思います。
C++ での実装例
AOJ GRL_2_A Minimum Spanning Tree を解く実装例です。グラフ \(G\) を与えられて、最小全域木の辺の重みの総和を求めます。
この問題のように、グラフが隣接リストで与えられる時はクラスカル法で実装しやすいですが、隣接行列で与えられる時はプリム法を用いたほうが実装しやすいです。
#include <bits/stdc++.h>
using namespace std;
/* UnionFind:素集合系管理の構造体(union by rank)
isSame(x, y): x と y が同じ集合にいるか。 計算量はならし O(α(n))
unite(x, y): x と y を同じ集合にする。計算量はならし O(α(n))
*/
struct UnionFind { // The range of node number is u 0 v n-1
vector<int> rank, parents;
UnionFind() {}
UnionFind(int n) { // make n trees.
rank.resize(n, 0);
parents.resize(n, 0);
for (int i = 0; i < n; i++) {
makeTree(i);
}
}
void makeTree(int x) {
parents[x] = x; // the parent of x is x
rank[x] = 0;
}
bool isSame(int x, int y) { return findRoot(x) == findRoot(y); }
void unite(int x, int y) {
x = findRoot(x);
y = findRoot(y);
if (rank[x] > rank[y]) {
parents[y] = x;
} else {
parents[x] = y;
if (rank[x] == rank[y]) {
rank[y]++;
}
}
}
int findRoot(int x) {
if (x != parents[x]) parents[x] = findRoot(parents[x]);
return parents[x];
}
};
// 辺の定義
struct Edge {
long long u;
long long v;
long long cost;
};
bool comp_e(const Edge &e1, const Edge &e2) { return e1.cost < e2.cost; } // 辺を直接比較するための関数
/* Kruskal :クラスカル法で minimum spanning tree を求める構造体
入力: 辺のvector, 頂点数V
最小全域木の重みの総和: sum
計算量: O(|E|log|V|)
*/
struct Kruskal {
UnionFind uft;
long long sum; // 最小全域木の重みの総和
vector<Edge> edges;
int V;
Kruskal(const vector<Edge> &edges_, int V_) : edges(edges_), V(V_) { init(); }
void init() {
sort(edges.begin(), edges.end(), comp_e); // 辺の重みでソート
uft = UnionFind(V);
sum = 0;
for (auto e : edges) {
if (!uft.isSame(e.u, e.v)) { // 閉路にならなければ加える
uft.unite(e.u, e.v);
sum += e.cost;
}
}
}
};
int main() {
int V, E;
cin >> V >> E;
vector<Edge> edges(E);
for (int i = 0; i < E; i++) {
long long s, t, w;
cin >> s >> t >> w;
Edge e = {s, t, w};
edges[i] = e;
}
Kruskal krs(edges, V);
cout << krs.sum << endl;
return 0;
}
クラスカル法の気持ち
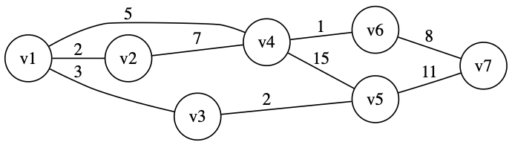
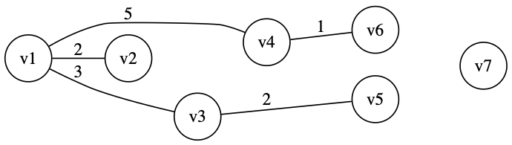
以下のグラフ \(G\) の最小全域木をクラスカル法で求めてみます。

・辺 (v4,v6) のコスト 1 が最小。閉路ができないので加える。

・辺 (v1,v2) のコスト 2 が最小。閉路ができないので加える。
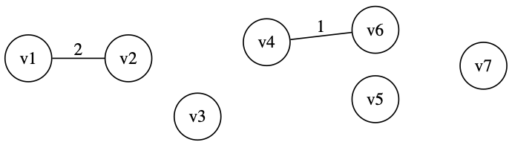
・辺 (v3,v5) のコスト 2 が最小。閉路ができないので加える。
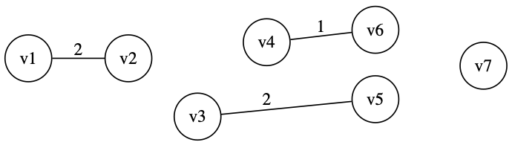
・辺 (v1,v3) のコスト 3 が最小。閉路ができないので加える。
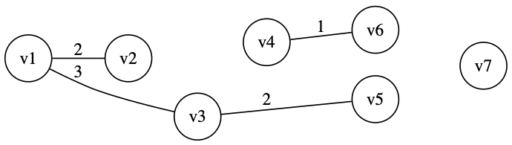
・辺 (v1,v4) のコスト 5 が最小。閉路ができないので加える。
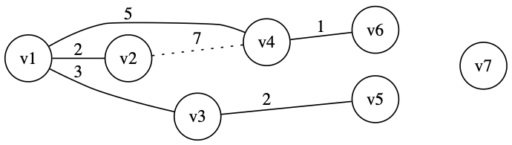
・辺 (v2,v4) のコスト 7 が最小。閉路ができてしまうので加えない
・辺 (v6,v7) のコスト 8 が最小。閉路ができないので加える。

以上で、全頂点を含んだ木ができたので、これが最小全域木となります。
ディスカッション
コメント一覧
まだ、コメントがありません