[AtCoder] キーエンスプログラミングコンテスト2020 D – Swap and Flip (700点)
問題
表が\(A_i\)、裏が\(B_i\)、と書かれた\(N\)枚のカードがある。「隣り合う2枚を選択して、入れ替えて裏返す」という操作をして、カードの並びが広義単調増加になる最小回数を求めよ。
制約
- \( 1 \leq N \leq 18\)
- \( 1 \leq A_i, B_i \leq 50 ~ (1\leq i \leq N)\)
考え方その1(DP)
制約が特殊なので、どのような計算量になるかの想像はしやすいでしょう。\(N\)が20前後の時は\(O(2^N)\)が関係してくることが多いです。
ひとまず全探索することを考えてみます。カードの並べ方は\(N!\)通りあるので、実際にこの通り並べてみて、広義単調増加になっている物の中でswap回数が最小のものを見つければ良いです。
i番目のカードが何回か操作を行った後にj番目に来たとき、表面にある数は
- |i-j| が偶数→\(A_i\)
- |i-j| が奇数→\(B_i\)
となっています。全てのカードについて\(A_i\)か\(B_i\)なのかを考えれば、カードが広義単調増加になっているのかを\(O(N)\)もあれば判定できます。
しかし、\(N!\)通りの全探索は今回の制約では間に合わないので何らかの工夫が求められます。今回のように隣接swap系の問題は似たようなDPで解けることが多いようです。
dp[S][last]:=集合Sで表されるカードを、左に詰めてソートした時の最小のswap回数(転倒数)。
ただし、最後に加えたものの値をlastとする。
とするとうまくできます。
dp の更新式を考える前に、動的計画法を使わずにdp[S][last]をどのように求めたらよいか考えてみます。Sが分かっていれば、swap回数は以下のように計算できます。
- まだSから選択していないものの中で、最小の要素のうち、一番前にあるものを選ぶ
- 先頭に来るようにswapする
- 1に戻る
つまり、選択ソートのようにしてやれば、Sから最小のswap回数を求めることができます。
dp の更新式は、このソートをイメージするとわかりやすいです。つまり、ソートされた部分の一番最後は、一番最後に選択される必要があります。
解法
dp[S][last]:=集合Sで表されるカードを、左に詰めてソートした時の最小のswap回数(転倒数)。
ただし、最後に加えたものの値をlastとする。
dp[S][ last ]に新たにカード i を加えて更新するとき、カード i は S の一番最後に置かれる時のみを考えれば良いです。つまり更新式は以下の通りです。
dp[S かつ i ][ i_val ] ← min( dp[S かつ i ][ i_val ], dp[S][ last ] + | now – |S| | )
ただし i_val \(\geq\) lastのとき
ここでの i_valは以下のような値です。
- abs(i – |S|) % 2 == 0のとき:A[i]
- abs(i – |S|) % 2 == 1のとき:B[i]
#include <bits/stdc++.h>
#define REP(i, n) for (int i = 0; i < (n); i++)
#define RREP(i, n) for (int i = (n); i >= 0; i--)
#define FOR(i, m, n) for (int i = (m); i < (n); i++)
#define ALL(obj) begin(obj), end(obj)
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int INF = 2100100100;
const int MOD = 1e9 + 7;
template <class T> bool chmax(T &a, const T &b) {
if (a < b) {
a = b;
return 1;
}
return 0;
}
template <class T> bool chmin(T &a, const T &b) {
if (b < a) {
a = b;
return 1;
}
return 0;
}
int dp[500000][55];
int main() {
// cin.tie(0);
// ios::sync_with_stdio(false);
int N;
cin >> N;
vector<int> A(N), B(N);
REP(i, N) { cin >> A.at(i); }
REP(i, N) { cin >> B.at(i); }
// 初期化
REP(bit, 1 << N) {
REP(i, 55) { dp[bit][i] = INF; }
}
dp[0][0] = 0;
REP(bit, 1 << N) {
int S_size = 0;
REP(i, N) {
int mask = 1 << i;
if (bit & mask) {
S_size++;
}
}
vector<pair<int, int>> invS; // first:もともと何番目か、second:カードの現在地
int now = S_size;
REP(i, N) {
int mask = 1 << i;
if ((bit & mask) == 0) {
invS.emplace_back(i, now);
now++;
}
}
// cout << "bit:" << bit << endl;
REP(last, 51) {
for (auto v : invS) {
int i = v.first;
int now = v.second;
int i_val;
if (abs(i - S_size) % 2 == 0) {
i_val = A[i];
} else {
i_val = B[i];
}
if (i_val >= last) {
chmin(dp[bit | (1 << i)][i_val], dp[bit][last] + abs(now - S_size));
}
}
}
}
int ans = INF;
REP(i, 55) { chmin(ans, dp[(1 << N) - 1][i]); }
if (ans == INF) {
cout << -1 << endl;
} else {
cout << ans << endl;
}
return 0;
}
考え方その2(表か裏かを最初に決める)
別の考え方もあります。先に各カードごとに、表(\(A_i\))になるのか裏(\(B_i\))になるのかを決めてしまうと、これは\(O(2^N)\)通りあります。あとは、
- 表(\(A_i\))→ |i-j| が偶数
- 裏(\(B_i\))→ |i-j| が奇数
- カードの並びが広義単調増加
を満たすように並べられるかを判定し、転倒数を求めればOKです。
これの判定が難しく、適当にやるとWAになってしまいます。
例えば、バブルソートをしてから偶奇性を満たすかどうか判定すると、同じ数がいくつかある時にWAになる可能性があります。
裏表を決め打ちすると、最終的に遷移先(j) が偶数番目になるのか奇数番目になるのかが決定されます。以下のような同じ数がいくつか登場する場合では、正しい並べ方が存在する時でも、それとバブルソートでの並べ方が異なる可能性があります。
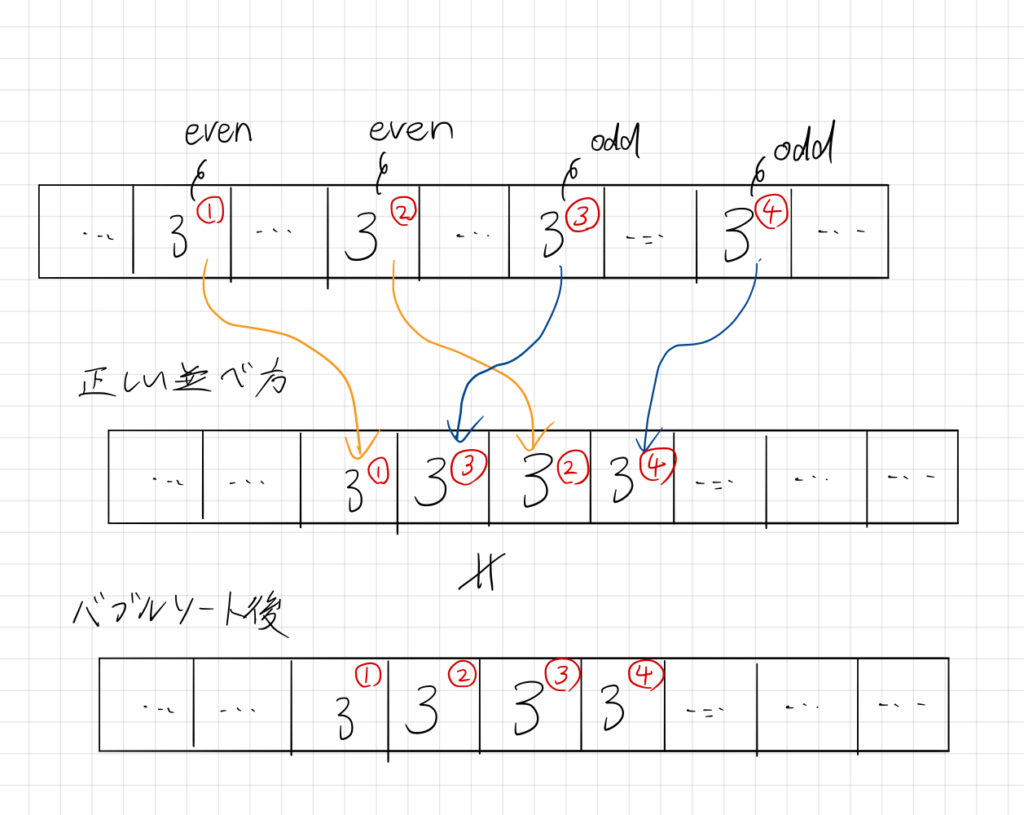
つまり、同じ数が複数ある時は、広義単調増加であるような並べ方が複数存在することになるので、先に全体の並び方を決定して偶奇性を確認するためには、全ての並べ方を確認する必要があります。(先程の例では1つしか確認していない)。
逆に、偶奇性を必ず満たすように、偶数の物と奇数の物に分けてソートしてやれば、正しい並べ方が存在するならそれと同じになり、存在しない場合は全体として広義単調増加になりません。これなら1通りの確認で済みます。
正しい判定を行うためには、正しい並べ方をすると、
- 偶数番目だけ考えても広義単調増加
- 奇数番目だけを考えても広義単調増加
- 全体で考えても広義単調増加
となっていることに注目すると良いです。
解法
まず各カードごとに、表(\(A_i\))になるのか裏(\(B_i\))になるのかを決めます。
最終的に偶数番目になるのは\([(N + 1) / 2]\)枚、裏になるものは\([N / 2]\)枚であるので、これを満たすものだけについて考えましょう。
条件を満たすような並べ方ができるかを判定するためには、
- 最終的に偶数番目に到達するものでソート
- 最終的に奇数番目に到達するものでソート
- 全体で広義単調増加になっているかを判定し転倒数を計算
とすれば良いです。
#include <bits/stdc++.h>
#define REP(i, n) for (int i = 0; i < (n); i++)
#define RREP(i, n) for (int i = (n); i >= 0; i--)
#define FOR(i, m, n) for (int i = (m); i < (n); i++)
#define ALL(obj) begin(obj), end(obj)
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int INF = 2100100100;
const int MOD = 1e9 + 7;
template <class T> bool chmax(T &a, const T &b) {
if (a < b) {
a = b;
return 1;
}
return 0;
}
template <class T> bool chmin(T &a, const T &b) {
if (b < a) {
a = b;
return 1;
}
return 0;
}
int main() {
// cin.tie(0);
// ios::sync_with_stdio(false);
int N;
cin >> N;
vector<int> A(N), B(N);
REP(i, N) { cin >> A.at(i); }
REP(i, N) { cin >> B.at(i); }
int ans = INF;
int bit = 0;
REP(bit, 1 << N) {
vector<pair<int, int>> even, odd;
int mask = 1;
REP(i, N) {
if (mask & bit) { // ビットが立てば裏
if (i % 2 == 0) {
odd.push_back(make_pair(B[i], i));
} else {
even.push_back(make_pair(B[i], i));
}
} else {
if (i % 2 == 0) {
even.push_back(make_pair(A[i], i));
} else {
odd.push_back(make_pair(A[i], i));
}
}
mask = mask << 1;
}
// 遷移先が偶数になるものは (N + 1) / 2 枚、奇数は N / 2 枚
if (!((even.size() == (N + 1) / 2) && (odd.size() == N / 2))) {
continue;
}
// 偶奇で分けてソート
sort(ALL(even));
sort(ALL(odd));
// 全体として広義単調増加か確認
vector<pair<int, int>> whole;
REP(i, N) {
if (i % 2 == 0) {
whole.push_back(even[i / 2]);
} else {
whole.push_back(odd[i / 2]);
}
}
bool flag = false;
REP(i, N - 1) {
if (whole[i].first > whole[i + 1].first) {
flag = true;
break;
}
}
if (flag) {
continue;
}
// 転倒数の計算(もとの並び方に戻して計算する)
int t = 0;
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N - i - 1; j++) {
if (whole[j].second > whole[j + 1].second) {
swap(whole[j], whole[j + 1]);
t++;
}
}
}
chmin(ans, t);
}
if (ans == INF) {
cout << -1 << endl;
} else {
cout << ans << endl;
}
return 0;
}
ディスカッション
コメント一覧
まだ、コメントがありません