グラフの連結成分の個数を求めるアルゴリズム

2020年3月20日2020年9月2日グラフ幅優先探索,グラフ,深さ優先探索,連結成分,連結成分の数

連結成分とは、「任意の2頂点間にパスが存在するような部分グラフのうち極大なもの」のことを言います。

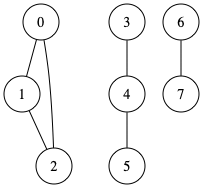
アルゴリズム

連結成分の個数はDFSやBFSで簡単に求めることができます。1つの連結成分は、1回のDFSやBFSで探索することができるからです。

計算量

• \(O(|V|+|E|)\)

全体において各頂点が未探索かどうか調べるので \(O(|V|)\)だけかかり、DFS や BFS で各辺について調べることになるので \(O(|E|)\) の計算量になります。合わせて \(O(|V|+|E|)\) です。

C++ での実装例

頂点数 n 、辺の数 m となる無向グラフの連結成分を DFS で数えるコードです。

#include <bits/stdc++.h>
using namespace std;

struct Edge {
    int to;
};
using Graph = vector<vector<Edge>>;

// 深さ優先探索
vector<bool> seen;  // 探索したか記録
void dfs(const Graph &G, int v) {
    seen[v] = true;
    for (auto e : G[v]) {
        if (!seen[e.to]) {  // 訪問済みでなければ探索
            dfs(G, e.to);
        }
    }
}

int main() {
    int n, m;
    cin >> n >> m;

    Graph G(n);
    for (int i = 0; i < m; i++) {
        int a, b;
        cin >> a >> b;
        G[a].push_back({b});
        G[b].push_back({a});
    }

    seen.assign(n, false);  // 初期化
    int cnt = 0; 
    for (int i = 0; i < n; i++) {
        if (!seen[i]) {
            dfs(G, i);
            cnt++; // dfsした回数をカウント
        }
    }
    cout << cnt << endl;

    return 0;
}