グラフにおける関節点(Articulation Points)を検出するアルゴリズム

2020年2月15日2020年9月2日グラフグラフ,競プロ,関節点,切断点,橋,lowlink,DFS,検出

連結グラフにおける関節点(切断点)とは、「グラフから取り除くと、グラフが非連結になってしまうような頂点」のことを言います。

※「連結」とは任意の2頂点間を行き来できることを言い、「非連結」は逆に行き来できない頂点があることを言います。（くわしくはグラフを参照）

以下の図における赤い頂点が関節点です。

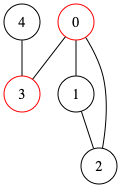
非連結グラフにおいては、「グラフから取り除くと、グラフの連結成分の数が増える頂点」を関節点と呼びます。

アルゴリズム

※ DFS tree (深さ優先探索木)は、DFSでグラフを探索する際に通る辺や頂点の集合のことです。これは木になっています。

※ 上述のアルゴリズムは、以下の「頂点 u が関節点となる条件」が元になっています。

• 以下の2つのどちらかが成立すれば u は関節点
  1. u が DFS tree の根(root) で、u は少なくとも 2 つの子を持つ
  2. u が DFS tree の根(root) でなく、子として以下を満たす頂点 v を持つ
     • v を根とする DFS tree の部分木において、u の祖先への後退辺を持つ頂点が存在しない

※ ある辺 (u,v)が橋(bridge)であるときは、ord[u] < low[v] を満たします。

計算量

• 単純なアルゴリズム：O(V(V+E))
• lowlink を用いたアルゴリズム：O(V+E)

C++での実装例 (lowlink)

struct Edge {
    int to;
};
using Graph = vector<vector<Edge>>;
using P = pair<long, long>;

/* Lowlink: グラフの関節点・橋を列挙する構造体
    作成: O(E+V)
    関節点の集合: vector<int> aps
    橋の集合: vector<P> bridges
*/
struct LowLink {
    const Graph &G;
    vector<int> used, ord, low;
    vector<int> aps;  // articulation points
    vector<P> bridges;

    LowLink(const Graph &G_) : G(G_) {
        used.assign(G.size(), 0);
        ord.assign(G.size(), 0);
        low.assign(G.size(), 0);
        int k = 0;
        for (int i = 0; i < (int)G.size(); i++) {
            if (!used[i]) k = dfs(i, k, -1);
        }
        sort(aps.begin(), aps.end()); // 必要ならソートする
        sort(bridges.begin(), bridges.end()); // 必要ならソートする
    }

    int dfs(int id, int k, int par) { // id:探索中の頂点, k:dfsで何番目に探索するか, par:idの親
        used[id] = true;
        ord[id] = k++;
        low[id] = ord[id];
        bool is_aps = false;
        int count = 0; // 子の数
        for (auto &e : G[id]) {
            if (!used[e.to]) {
                count++;
                k = dfs(e.to, k, id);
                low[id] = min(low[id], low[e.to]);
                if (par != -1 && ord[id] <= low[e.to]) is_aps = true; // 条件2を満たすので関節点
                if (ord[id] < low[e.to]) bridges.emplace_back(min(id, e.to), max(id, e.to));  
            } else if (e.to != par) { // eが後退辺の時
                low[id] = min(low[id], ord[e.to]);
            }
        }
        if (par == -1 && count >= 2) is_aps = true; // 条件1を満たすので関節点
        if (is_aps) aps.push_back(id);
        return k;
    }
};

アルゴリズム(lowlink)の考え方と正当性

深さ優先探索(DFS) でグラフを探索することを考えます。DFSでグラフを探索する際に通る辺や頂点を考えると、これは木になっています。この木を DFS tree (深さ優先探索木)と呼ぶことにしましょう。

DFS tree で用いられなかった辺を「後退辺」と言います。

DFS tree において、以下の2つの条件のうちどちらかが成立すれば、頂点 u が関節点であると言えます。

1. u が DFS tree の根(root) で、u は少なくとも 2 つの子を持つ
2. u が DFS tree の根(root) でなく、子として以下を満たす頂点 v を持つ
   • v を根とする DFS tree の部分木において、u の祖先への後退辺を持つ頂点が存在しない

下の図で言えば、頂点1 が条件1・頂点2 が条件2 を満たすので、この2つが関節点です。後退辺は、頂点2と頂点4の間にある辺だけです。

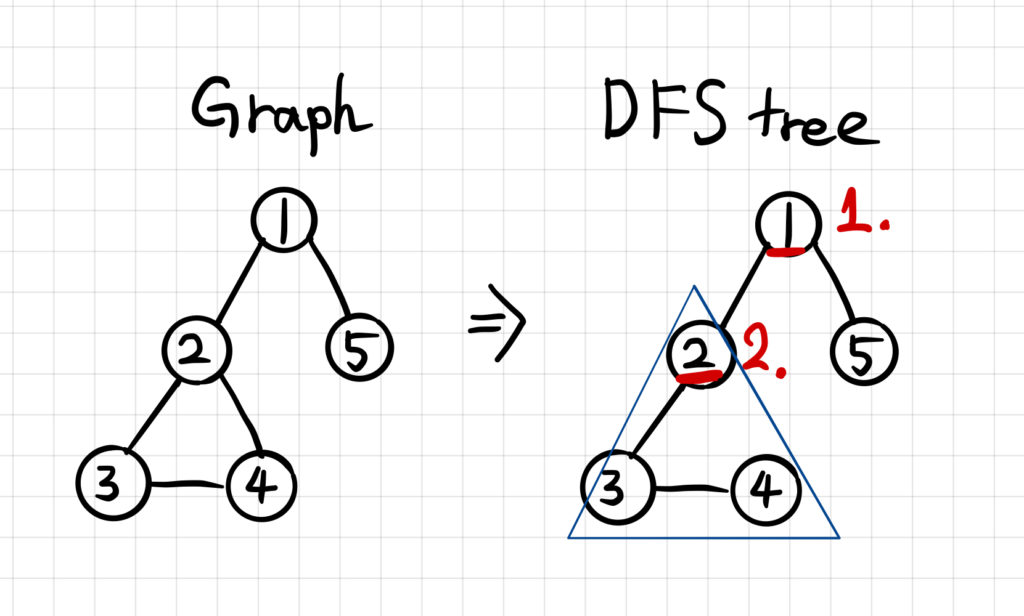
アルゴリズムとするために、DFS で関節点のための値を取得しましょう。

• ord[u] : DFS で頂点 u を何番目に探索したか
• low[u] : u からの後退辺を高々1回まで用いて到達できる頂点 w について、ord[w] の最小値

以上の値を利用すると、u が関節点となる条件は以下のようになります。

1. u が DFS tree の根(root) の時、子が2つ以上存在する
2. u が DFS tree の根(root) でない時、頂点 u のある子 v について ord[u] ≤ low[v] を満たす

この low[u] のことを lowlink などと言います。

グラフ上での関節点の意味

グラフをネットワークとして考えると、関節点はネットワーク上の脆弱性を表現しています。関節点に障害が発生すると、ネットワーク全体が非連結となってしまうのです。

故に関節点は信頼性のあるネットワークをデザインする際に考慮されます。

練習問題

• AOJ GRL_3_A Articulation Points