[AtCoder] ABC154 F – Many Many Paths (600点)
問題概要
2次元の平面上で、以下のように関数 f(r,c) を定義する。
f(r,c) := (0,0)から(r,c)までの経路の個数
この時、以下を計算せよ。ただし、\(10^9+7\) で割った余りで求めよ。
$$ \sum_{i=r_1}^{r_2}\sum_{j=c_1}^{c_2} f(i,j)$$
制約
- \(1 \leq r_1 \leq r_2 \leq 10^6\)
- \(1 \leq c_1 \leq c_2 \leq 10^6\)
考え方
問題は、以下のような平面上での区間和を求める問題とも言えます。
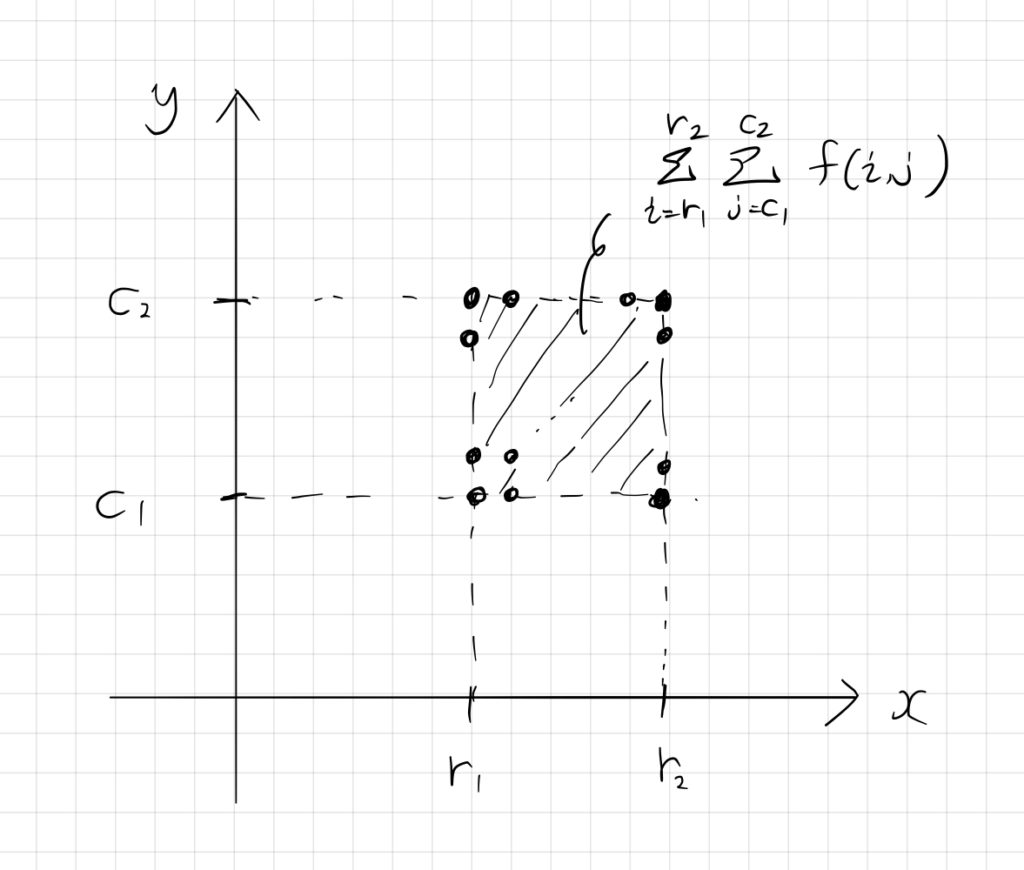
ここで
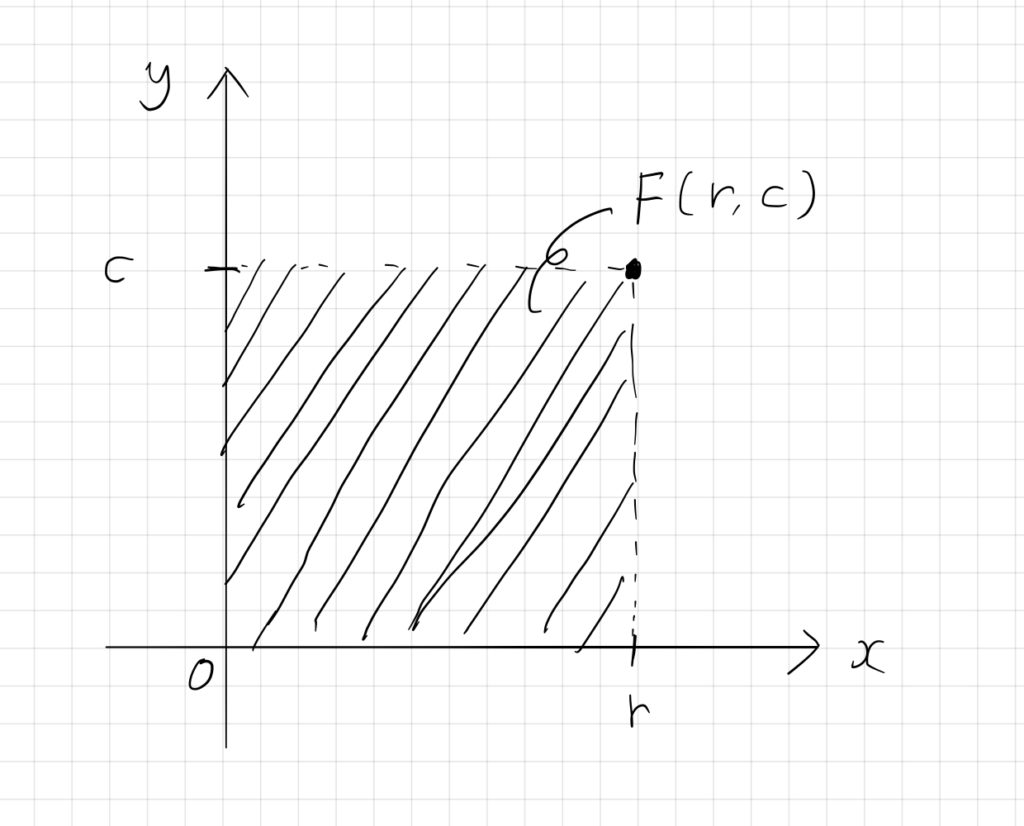
$$F(r,c) :=\sum_{i=0}^{r}\sum_{j=0}^{c} f(i,j)$$
と定義します。これは問題よりも簡単な二次元区間和です。
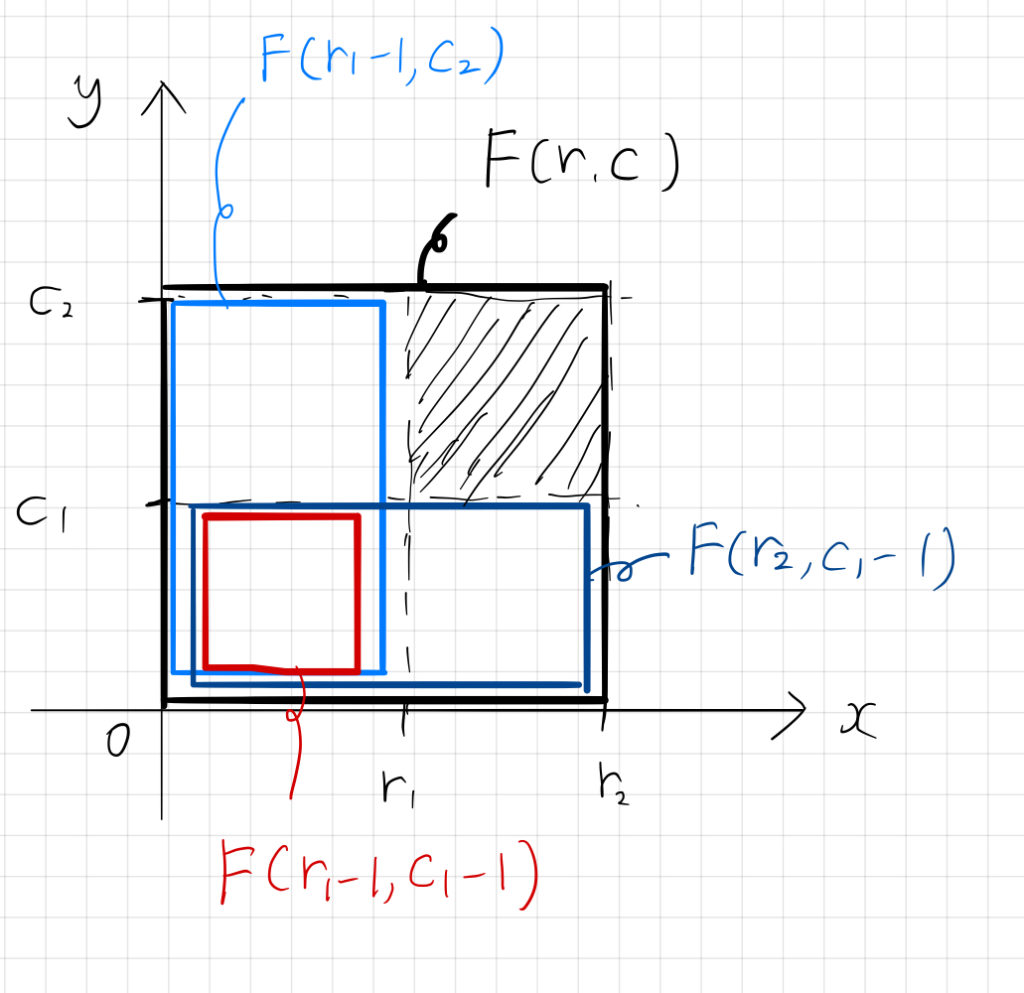
二次元区間和は、先程定義したような二次元区間和を4つ用いて計算することが多いです。つまり、
$$ F(r2,c2) – F(r1-1,c2) – F(r2, c1-1) + F(r1-1, c1 -1) $$
が答えになります。
解き方
先程定義した F(r,c) を高速に求めることができれば良いのが分かります。
以下の関係式を用いて式変形を行いましょう。
$$ f(i, j+1) = f(0, j) + f(1, j) + f(2, j) + \cdots + f(i, j) $$
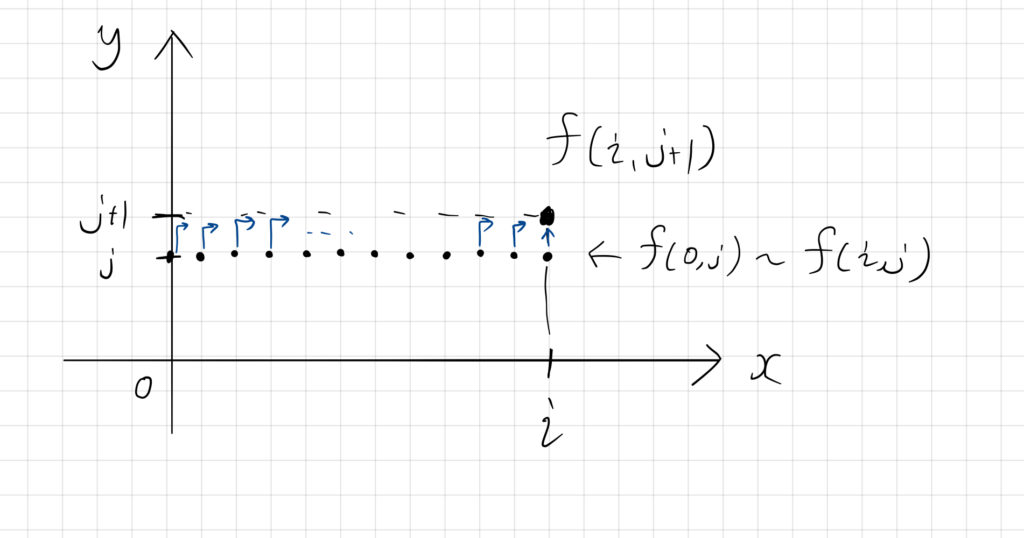
これを利用することで以下のように計算することができます。
$$ F(r,c) = \sum_{j=1}^{c+1} f(r,j)$$
これは、f(i,j) の計算は二項係数を用いると O(1)で計算ができるので、F(r,c)の計算は O(c) で計算をすることができます。（もう一度同様の式変形を用いると O(1)で求めることもできます）
実装例
#include <bits/stdc++.h>
#define LOOP(n) for (int _i = 0; _i < (n); _i++)
#define REP(i, n) for (int i = 0; i < (n); ++i)
#define FOR(i, r, n) for (int i = (r); i < (n); ++i)
#define ALL(obj) begin(obj), end(obj)
using namespace std;
const int MOD = 1e9 + 7;
vector<long long> fact, fact_inv, inv;
/* init_nCk :二項係数のための前処理
計算量:O(n)
*/
void init_nCk(int SIZE) {
fact.resize(SIZE + 5);
fact_inv.resize(SIZE + 5);
inv.resize(SIZE + 5);
fact[0] = fact[1] = 1;
fact_inv[0] = fact_inv[1] = 1;
inv[1] = 1;
for (int i = 2; i < SIZE + 5; i++) {
fact[i] = fact[i - 1] * i % MOD;
inv[i] = MOD - inv[MOD % i] * (MOD / i) % MOD;
fact_inv[i] = fact_inv[i - 1] * inv[i] % MOD;
}
}
/* nCk :MODでの二項係数を求める(前処理 int_nCk が必要)
計算量:O(1)
*/
long long nCk(int n, int k) {
assert(!(n < k));
assert(!(n < 0 || k < 0));
return fact[n] * (fact_inv[k] * fact_inv[n - k] % MOD) % MOD;
}
long long F(int r, int c) {
long long ret = 0;
FOR(j, 1, c + 2) {
ret += nCk(r + j, j);
ret %= MOD;
}
return ret;
}
int main() {
int r1, c1, r2, c2;
cin >> r1 >> c1 >> r2 >> c2;
init_nCk(4000000);
cout << (((F(r2, c2) + (MOD - F(r2, c1 - 1))) % MOD + (MOD - F(r1 - 1, c2))) % MOD + F(r1 - 1, c1 - 1)) % MOD
<< endl;
return 0;
}