再帰関数を用いた深さ優先探索(DFS)による全探索アルゴリズム

2020年5月10日探索

forループを用いた全探索などは比較的簡単な内容なので直感的にもわかりやすいですが、簡単なものしか全探索できません。

複雑な条件や構造を持つものを全探索したい場合には、再帰関数を用いた深さ優先探索(DFS)を用いる必要がある場合があり、競技プログラミングなどで良く出題されています。

前提知識

今回の内容を理解するために必要なことを簡単に説明しておきます。

再帰関数とは

再帰関数を詳しく考えようとするとコンピュータの仕組みまで考える必要があるので難しいです。簡単に言うと「自身を呼び出す関数」を再帰関数と呼びます。

「自身を呼び出す」たびに、どんどんと深くまで潜っていくようなイメージです。

再帰関数の流れ：

  1. 「再帰関数1」を呼び出す
  2. …何か処理をする…
  3. 「再帰関数1」 の中で「再帰関数2」を呼び出す
    1. 「再帰関数2」を呼び出す
    2. …何か処理をする…
    3. 「再帰関数2」 の中で「再帰関数3」を呼び出す
      • …
      • 何か条件を満たして終了するまで呼び出し続ける
      • …
    4. 「再帰関数3」が終了して「再帰関数2」に戻る
    5. …何か処理をする…
    6. 「再帰関数2」が終了
  4. 「再帰関数2」が終了して「再帰関数1」に戻る
  5. …何か処理をする…
  6. 「再帰関数1」が終了

簡単なプログラムでは必要の無いことが多いですし、バグらせやすくデバッグしにくいのであまり使用する機会がなかった方もいるかもしれません。

深さ優先探索とは

深さ優先探索は、「とりあえずこれ以上進めなくなるまで探索したら、戻って別のルートで探索し直す」ようなアルゴリズムです。

以下の図のように、 左から右へと番号順にたどると深さ優先探索になります。探索済みになり、もう右に進めなくなったら左に戻ります。

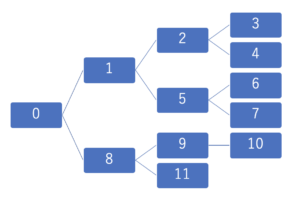
実装上では、一つの再帰関数内で、複数の再帰関数を呼び出すことで実現することができます。

グラフ上での探索でも用いられ、まずはそこを先に理解したほうがわかりやすいと思います。深さ優先探索(Depth First Search)の基本 を確認して下さい。

アルゴリズム

ある条件Pを満たした要素数Nの集合を全探索することを考えます。

全探索をする再帰関数 dfs(S)：

  • Sの要素数がNの時
    1. 何か処理をする
  • Sの要素数がN未満の時
    1. Sに加えても条件Pを満たすような要素 a 全てに対して以下を行う
      1. Sにa を加えたものを S’ とする
      2. dfs(S’) を呼び出す

※問題ごとに微妙に内容が異なる場合もありますが、基本は以上のようになります。

※イメージ的には、再帰が深くなるにつれて要素数が増えていき、末端にたどり着いた時に、条件Pを満たした要素数Nの集合になります。以下はビット全探索をDFSで行うときのイメージです。

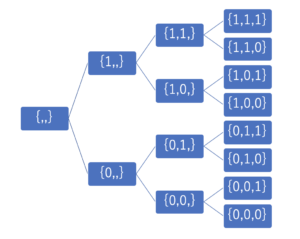
※ 実装する際に、 S に a を加えた S’ というものを実際に作成すると、余計にメモリや計算が必要になります。後述する問題の実装例のように、S の参照を渡して同じものをうまく使い回すと良いです。

計算量

計算量の見積もりは結構難しいです。条件Pや要素数Nの内容によって大きく異なってきます。全探索しようとしているものが何通りあるのかを考える必要があるでしょう。

仮に、一つの再帰関数で M 個に分岐するとしましょう。深さはNまでなので、再帰関数の呼び出し回数は \(O(M^N)\) 程度になります。よって、一つの再帰関数の処理が定数時間ならば、

  • \(O(M^N)\)

の計算量になります。

注意点

再帰が深くなりすぎると、スタックオーバーフローになる可能性があります。

コンピュータの能力などに注意する必要はありますが、競技プログラミングでは計算量の見積もりさえしっかりやっておけば大きく気にする必要はありません。

ただし、Python など、プログラミング言語によっては再帰の深さが制限されていることもあるそうです。

問題例：AtCoder ABC 114 C – 755

問題概要

整数 N が与えられます。1 以上 N 以下の整数のうち、以下の条件を満たすものは何個あるでしょうか？

  • 条件：十進法で表記したとき、数字 7, 5, 3 がそれぞれ 1 回以上現れ、これら以外の数字は現れない。

制約

  • \(1 \leq N < 10^9\)

考え方

もし N が小さければ、for 文などを用いることで、1~N までの数を全探索することができます。しかし、この問題では N が最大で \(10^9\) 程度なので間に合いません。

しかし、「7, 5, 3 のどれかのみが現れる数字」だけならば全探索をしても十分間に合います。この中から、「7,5,3 のそれぞれが1回以上現れる」ものを探せばよいのです。よって、ここでDFSを利用することができます。

桁数は最大でも 9 桁なので、\(3^9\) 程度の要素を全探索すれば終了です。

C++での実装例

C++での実装例です。Sをstring 型として参照渡しをすることで、余計なコピーが生まれずにメモリや計算量を節約することができます。

9桁目まで探索した場合には int 型を超えてオーバーフローしてしまう可能性があるので、long long 型として扱っています。

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll N;

// 深さ優先探索
int dfs(string &S) {
    ll ret = 0;
    vector<char> lis = {'3', '5', '7'};
    if ((int)S.size() > 0) {  // 最初はSは空なので注意
        if (stoll(S) > N) {   // Nを超えてたら探索しない
            return ret;
        } else {  // N 以下の時 3,5,7 がそれぞれ1回以上登場するか確かめる
            bool ok = true;
            for (auto c : lis) {
                if (S.find(c) == string::npos) ok = false;
            }
            if (ok) ret++;
        }
    }
    for (auto c : lis) {  // 3つに分岐する
        S.push_back(c);
        ret += dfs(S);
        S.pop_back();
    }
    return ret;
}

int main() {
    cin >> N;
    string S = "";
    cout << dfs(S) << endl;
}

練習問題

複雑な条件下での全探索を行いたい時にDFSを用いることが多いです。

探索