二部グラフの最大マッチングを求めるアルゴリズム
アルゴリズム
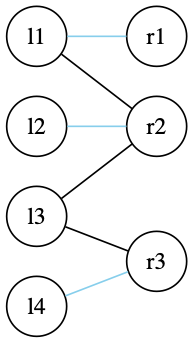
二部グラフの最大マッチングを求めるアルゴリズム:
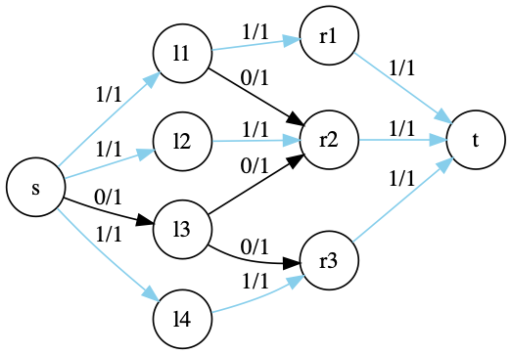
- 二部グラフ \(G=(L \cup R, E)\) に対応する以下のようなフローネットワーク \(G’\) を作る
- \(G\) にソース \(s\) とシンク \(t\) を加える
- \(s\) から \(L\) のすべての頂点に対して容量 1 の有向辺を加える
- \(R\) のすべての頂点から \(t\) に対して容量 1 の有向辺を加える
- \(L\) の頂点と \(R\) の頂点を結ぶ辺は、\(L\) から \(R\) への容量 1 の有向辺とする
- \(G’\) の最大フローを求めると、その流量は最大マッチングのサイズと一致する
※ マッチング \(M\) は、\(|M| = |f|\) となる1つの整数フロー \(f\) に対応します
※ マッチングの各ペアは、ソースからシンクへの流量1の部分的なフローに対応します
※ 最大フローを求めるアルゴリズムの代表例としては、Ford-Fullkerson法などがあります。
計算量
- \(O(|V||E|)\)
\(G’\) の最大フロー \(f^*\) の値は \(|f^*| = O(\min(L, R))\) 程度です。最大フローを求めるのにFord-Fullkerson法を用いれば、計算量は \(O(|f^*||E|)\) になります。
C++ での実装例
AOJ GRL_7_A Bipartite Matching を解くコードです。最大フローを求めるのにFord-Fullkerson法を用いています。
#include <bits/stdc++.h>
using namespace std;
template <class T>
struct Edge {
int rev, from, to; // rev:逆向きの辺の番号
T cap, original_cap;
Edge(int r, int f, int t, T c) : rev(r), from(f), to(t), cap(c), original_cap(c) {}
};
template <class T>
struct Graph {
vector<vector<Edge<T>>> G;
Graph(int n = 0) : G(n) {}
vector<Edge<T>>& operator[](int i) { return G[i]; }
const size_t size() const { return G.size(); }
Edge<T>& redge(Edge<T> e) { // 逆向きの辺を返す
return G[e.to][e.rev]; // 自己ループはないと仮定(あれば G[e.to][e.rev + 1] とする必要がある)
}
void add_edge(int from, int to, T cap) { // 有向辺を加える
G[from].push_back(Edge<T>((int)G[to].size(), from, to, cap));
G[to].push_back(Edge<T>((int)G[from].size() - 1, to, from, 0));
}
};
/* FordFulkerson: Ford-Fulkersonのアルゴリズムで最大流を求める構造体
max_flow(G,s,t) :グラフGの最大流が求まる
副作用:G は最大流の残余ネットワークになる
計算量: O(|f*||E|) (f*:最大流)
*/
template <class T>
struct FordFulkerson {
const T INF = 1e9;
vector<int> used;
FordFulkerson(){};
T dfs(Graph<T>& G, int v, int t, T f) { // 増加可能経路を見つけて増加分のフローを返す
if (v == t) return f;
used[v] = true;
for (auto& e : G[v]) {
if (!used[e.to] && e.cap > 0) {
T d = dfs(G, e.to, t, min(f, e.cap));
if (d > 0) {
e.cap -= d;
G.redge(e).cap += d;
return d;
}
}
}
return 0;
}
T max_flow(Graph<T>& G, int s, int t) {
T flow = 0;
while (true) {
used.assign(G.size(), 0);
T f = dfs(G, s, t, INF); // f が増加分のフロー
if (f == 0) {
return flow;
} else {
flow += f;
}
}
return 0;
}
};
int main() {
int X, Y, E;
cin >> X >> Y >> E;
Graph<int> G(X + Y + 2);
for (int i = 0; i < X; i++) { // ソース(0)から X(1~X) への辺
G.add_edge(0, i + 1, 1);
}
for (int i = 0; i < E; i++) { // X(1~X) から Y(X+1~X+Y) への辺
int x, y;
cin >> x >> y;
G.add_edge(x + 1, y + X + 1, 1);
}
for (int i = 0; i < Y; i++) { // Y(X+1~X+Y) からシンク(X+Y+1)への辺
G.add_edge(i + X + 1, X + Y + 1, 1);
}
FordFulkerson<int> ff;
cout << ff.max_flow(G, 0, X + Y + 1) << endl;
}
アルゴリズムの正当性
- \(G\) でのマッチング \(M\) が最大マッチング \(\Leftrightarrow\) \(M\) に対応する \(G’\) での整数フロー \(f\) が最大フロー
であることが示せれば良いです。
準備
以下の2つを用いて証明を行います。
\(G\) のマッチング \(M\) が存在するなら、\(G’\) において \(|f|=|M|\) となる整数フロー \(f\) が存在する。
逆に\(G’\) において整数フロー \(f\) が存在するなら、\(G\) において \(|f|=|M|\) となるマッチング \(M\) が存在する。
容量関数 \(c\) が整数値しか取らないなら、最大フロー \(f^*\) の値 \(|f^*|\) が整数値になり、任意の頂点 \(u,v\) について \(f(u,v)\) の値も整数値になる。
証明の概要
必要条件と十分条件に分けて示しましょう。
まずは \(G\) でのマッチング \(M\) が最大マッチングのときを考えます。\(M\) に対応する整数フロー \(f\) が存在するので、これが最大フロー \(f^*\) でないと仮定して矛盾を導けば良いです。
\(f^*\) は整数性定理から整数フローとなります。よってこれに対応するマッチング \(M^*\) を考えると、\(|M^*| = |f^*| > |f| = |M|\) となり \(M\) が最大マッチングであることと矛盾します。
逆も同様に示すことができます。
ディスカッション
コメント一覧
まだ、コメントがありません