マージソート(Merge Sort)

2019年11月24日ソート入門,ソート,マージソート,分割統治法

マージソートとは

マージソートは分割統治法を用いたソートアルゴリズムの1つです。配列を2分割することを繰り返し、小さい配列を一つ一つソートしてから「マージ(併合)」することで、最終的に高速にソートができます。

最終的に1つの要素になるまで分割すれば、ソート済みの長さ1の配列を得ることができるので、あとは「マージ」していくだけでソートが完了します。

アルゴリズム

マージソートは配列を2分割し、それぞれに対してマージソートをするので再帰関数となります。また、2つのソート済み配列を「マージ(併合)」して1つのソート済み配列を作る merge() 関数を使う必要があります。

配列の \(l\) 番目から \(r\) 番目までをソートする merge_sort(arr[], l, r) のアルゴリズムは以下のようになります。

  1. \(mid = (l+r)/2\) とする
  2. merge_sort(\(arr[], l, mid\)) で \(l\) 番目から \(mid\) 番目までソート
  3. merge_sort(\(arr[], mid+1, r\)) で \(mid+1\) 番目から \(r\) 番目までソート
  4. merge(\(arr[], l, mid, r\)) で先程ソートした配列をマージしながらソート

merge() 関数は、2つの配列の最小の要素をそれぞれ比べて、小さい方の要素を配列から取り出して並べていくだけです。

計算量

時間計算量(time complexity)

最悪・平均・最善の計算時間は \(O(n \log n)\) となります。これは \(O(n^2)\) と比べると非常に高速です。

領域計算量 (space complexity)

merge() 関数は、配列の長さ \(n\) のオーダーで新しいメモリが必要となってしまいます。これにより消費メモリは \(O(n)\) となります。

問題例

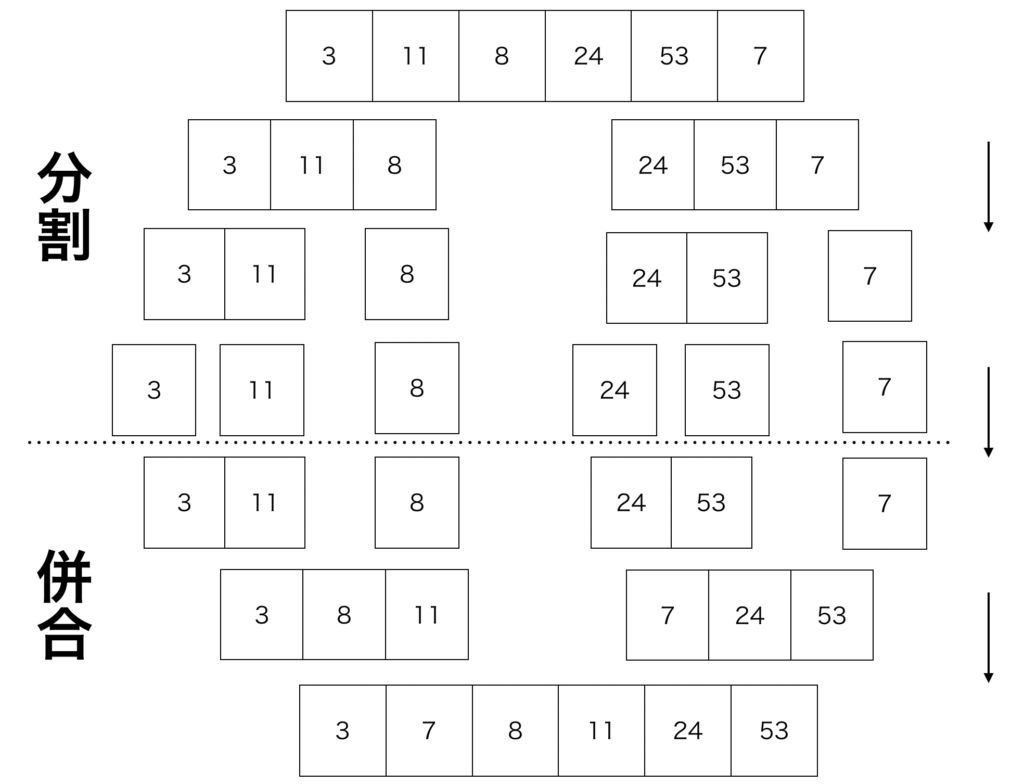
\(\{3,11,8,24,53,7\}\) と並んだ配列をマージソートする例を考えてみます。以下の図のように分割して、併合するとマージソートの完了です。

Pythonでのプログラム例

def merge(arr,l,mid,r): # マージする関数
  # ここで配列の一部を2つにコピー。メモリを余分に使うので外部ソートとなる
  arr1 = arr[l:mid] 
  arr2 = arr[mid:r]
  # arr1, arr2 のindex
  index1 = 0
  index2 = 0
  # もとのarrのindex
  index = l
  while index1<len(arr1) and index2<len(arr2): 
    if arr1[index1]<arr2[index2]:
      arr[index] = arr1[index1]
      index1 += 1
    else:
      arr[index] = arr2[index2]
      index2 += 1 
    index +=1

  while index1<len(arr1): 
      arr[index] = arr1[index1]
      index1 += 1
      index +=1

  while index2<len(arr2): 
      arr[index] = arr2[index2]
      index2 += 1
      index +=1

def merge_sort(arr,l,r): # マージソートする再帰関数
  if r-l>1:
    mid = l + (r-l)//2 # (l+r)//2 でも良いですが、こうするとオーバーフローを避けられます
    merge_sort(arr,l,mid)
    merge_sort(arr,mid,r)
    merge(arr,l,mid,r)

arr = [3,11,8,24,53,7]
merge_sort(arr, 0, len(arr))
print(arr)

ソート入門,ソート,マージソート,分割統治法